基于ABAQUS的动水压力波双渐近透射边界单元及应用
2019-10-19高毅超
高毅超,梅 真
(1.华侨大学 土木工程学院,福建 厦门 361021;2.福建省结构工程与防灾重点实验室,福建 厦门 361021)
在强震作用下,大坝与库水之间发生的显著动力相互作用将给大坝的动力响应带来重大影响。其中,如何准确模拟动水压力波在半无限库水中传播引起的辐射阻尼效应是该研究领域的热点和难点。在大坝-库水动力相互作用分析中,有限元法是有效的数值方法,但是需要在计算域的截断边界施加人工边界以避免波动的虚假反射,或者与其他无限域数值方法耦合以考虑无限介质辐射阻尼的影响。Küçükarslan等[1]结合有限元法和Sommerfeld辐射边界提出了结构-流体动力相互作用的数值分析方法,但是Sommerfeld辐射边界在理论上仅仅具有零阶精度,需要增加近场域离散范围以获得良好的计算精度。边界元法[2-3]只需离散边界使得问题维数降低一维,并且能够自动满足无穷远处的辐射边界条件,因而也被应用于结构-流体动力相互作用分析。然而边界元求解所需的基本解可能十分复杂或者不存在,大大限制了边界元在实际工程中的应用。
比例边界有限单元法(Scaled Boundary Finite Element Method,SBFEM)是Song等[4]提出的一种半解析数值方法,它只需离散边界而在径向保持解析,兼具有限元法和边界元法的优点。它不需要基本解即可自动满足无穷远处的辐射边界条件,因此非常适用于无限域动力问题的模拟。杜建国等[5]基于SBFEM提出了一种求解坝面动水压力的半解析方法;Lin等[6-8]将SBFEM应用于大坝-库水动力相互作用分析,然而其时域的求解均是基于耗时的卷积积分运算完成的。
高阶局部透射边界[9]具有高阶精度和较高的计算效率,然而绝大部分高阶透射边界属于高频单向渐近边界[10],无法同时模拟层状介质中行波和快衰波的传播。Prempramote等[11]基于动力刚度连分式双渐近解提出了一类高阶双渐近透射边界,随着渐近阶数的增加,该透射边界在全频范围内迅速收敛到准确解,具有很高的计算精度和计算效率。Wang等[12-14]结合SBFEM将该透射边界推广应用到层状库水的模拟,构建了动水压力波高阶双渐近透射边界,并建立了有限元-动水压力波高阶双渐近透射边界的时域耦合分析模型。数值算例分析结果表明,该耦合分析模型具有很高的计算精度和较高的计算效率。
ABAQUS是一套功能强大的通用有限元分析软件,它包括了丰富的单元库和材料模型库,并且具有良好的前后处理程序和强大的非线性方程求解器,在许多工程领域都得到了广泛应用。此外,ABAQUS提供了丰富的用户子程序接口,用户可以通过子程序接口自定义单元、材料、荷载和边界条件等,具有良好的可扩展性。
本文基于ABAQUS提供的用户子程序UEL接口,编写了动水压力波高阶双渐近透射边界单元,以超单元的形式直接将双渐近透射边界嵌入到近场有限元方程,实现了有限元-双渐近透射边界的时域直接耦合分析模型。通过数值算例验证双渐近透射边界单元程序编写的正确性,并将其应用到大坝-库水动力相互作用分析。
1 库水的比例边界有限单元方程
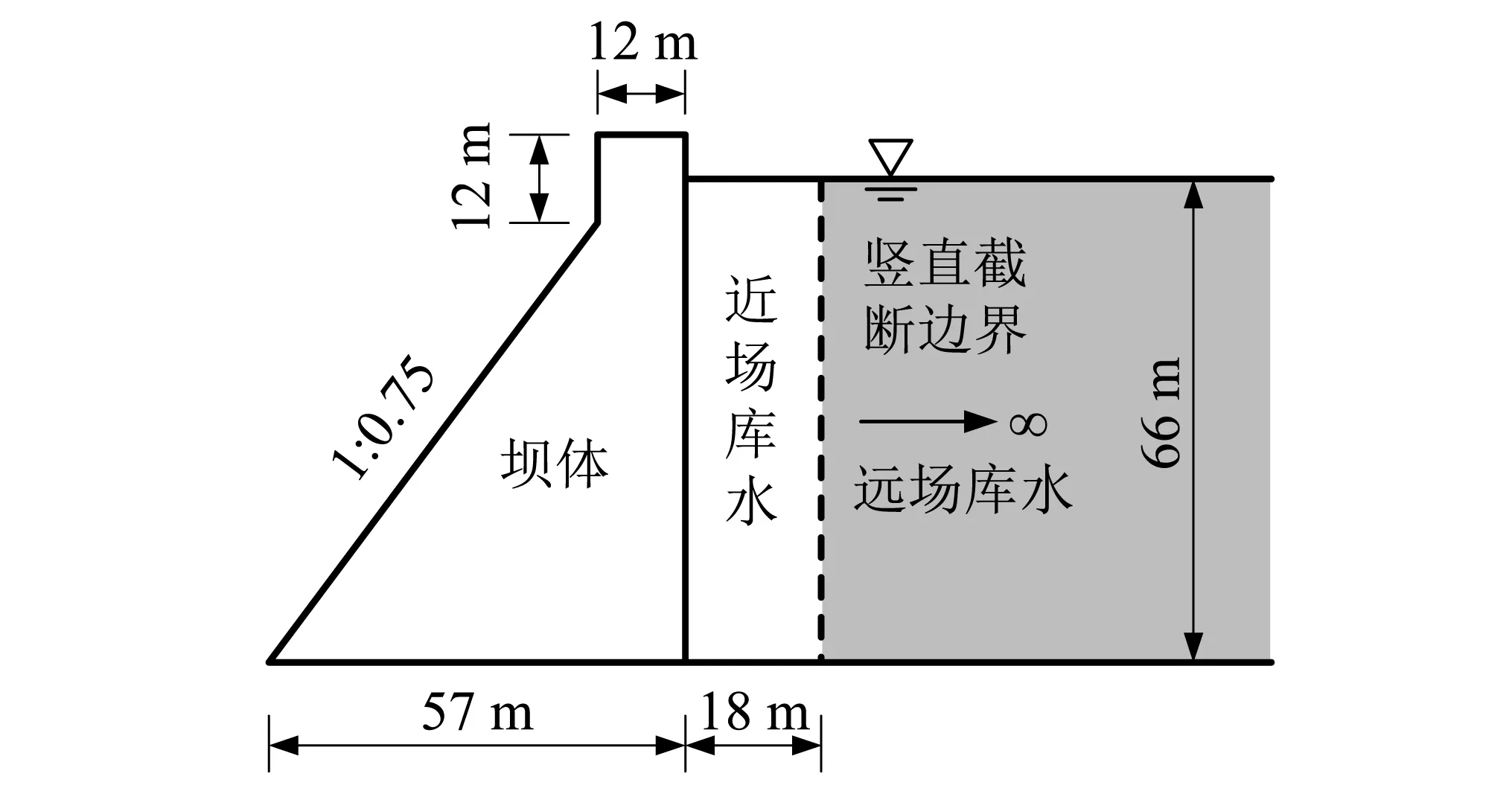
考虑如图1所示的典型大坝-库水系统,其中向上游无限延伸的层状库水被竖直截断边界分割成近场和远场两个部分。具有不规则几何形状的近场库水和坝体构成近场域采用有限单元离散;远场规则库水简化成半无限等截面层状介质,远场库水对近场域的辐射阻尼效应通过截断边界上的相互作用力-{r}表现。

图1 大坝-库水耦合系统Fig.1 A coupled dam-reservoir system
竖直截断边界采用比例边界有限单元离散,一个典型的单元如图2所示,其比例相似中心取在下游无穷远处。

图2 典型的比例边界有限单元Fig.2 A typical scaled boundary finite element
考虑竖直边界截断的半无限等截面层状库水,将库水视为理想声学流体介质,并且不考虑水库库底的吸收作用,动水压力表示的比例边界有限单元方程为
[E0]{p},ξξ-[E2]{p}-[M0]{p},tt=0
(1)
式中:{p}为动水压力;{p},ξξ为动水压力对比例边界坐标ξ的二次偏导;{p},tt为动水压力对时间的二次导数;系数矩阵[E0],[E2]和[M0]的定义为
(2)
(3)
(4)
式中:ρ和K分别为库水的密度和体积模量;[N]为单元插值函数,[B1],[B2]和|J|只与边界的几何信息有关,其定义详见Gao等的研究。对于等截面层状库水,[M0]和[E0]存在以下关系
[M0]=[E0]/c2
(5)

在频域内,截断边界上等效节点荷载{R(ω)}和节点动水压力{P(ω)}之间的关系可以用动力刚度[S∞(ω)]表示(其中ω表示频率),即
{R(ω)}=[S∞(ω)]{P(ω)}
(6)
在竖直边界上应用虚功原理,并考虑动力刚度的定义式(6),可以将式(1)改写成动力刚度表示的比例边界有限单元方程
[S∞(ω)][E0]-1[S∞(ω)]-[E2]+ω2[M0]=0
(7)
基于式(7),结合动力刚度的连分式渐近解和辅助变量技术,即可构建动水压力波高阶双渐近透射边界。
2 双渐近透射边界单元
对于等截面层状库水,动力刚度表示的比例边界有限单元方程可以通过模态变换的方式解耦,考虑如下广义特征值分解
[E2][Φ]=[E0][Φ][Λ2]/h2
[Φ]T[E0][Φ]=[I]
[Φ]T[E2][Φ]=[Λ2]/h2
(8)

(9)

(10)
根据Gao等的推导结果,动水压力波高阶双渐近透射边界在时域内的表达式为
(11)
(12)
(13)
(14)
(15)

(16)
(17)
式(17)即为高阶双渐近透射边界单元的控制方程,其中{ph}和{fh}分别为高阶双渐近透射边界单元的动水压力向量及荷载向量,定义分别为
(18)
{fh}={{r}T;{0}T;…;{0}T}T
(19)
单元刚度矩阵[Kh]和阻尼矩阵[Ch]分别为
(20)
(21)
式中:0为零矩阵,黑体字母表示分块矩阵,其定义分别为
(22)
双渐近透射边界单元的刚度矩阵、阻尼矩阵为常数矩阵,在分析过程中只需要计算一次,因此可以预先求解,再根据需要读入ABAQUS,提高计算效率。本文在程序实现上,将预先计算得到的双渐近透射边界单元的刚度矩阵和阻尼矩阵分别保存到两个二进制文件中,在ABAQUS调用UEL的过程中根据分析需要读取。
ABAQUS提供的用户子程序接口UEL采用FORTRAN语言编写,并在每一迭代步中被调用。用户在UEL中需要定义的变量主要包括AMATRX(刚度矩阵、质量矩阵等)和RHS(右端荷载向量)。本文在UEL的框架下,编写了双渐近透射边界单元子程序UEL_DAOB.for,其程序流程如下:
步骤1 初始化变量;
步骤2 从二进制文件中读取单元刚度矩阵和阻尼矩阵;
步骤3 根据标志变量IFLAGS(1)的取值,组装矩阵AMATRX和右端荷载向量RHS,并返回ABAQUS计算主程序。
3 算 例
3.1 重力坝算例
考虑一个典型的重力坝-库水系统,重力坝坝高72 m,近场库离散范围取18 m(约为1/4库水深度),其几何模型参数和有限元网格如图3所示。重力坝和近场库水均采用4节点四边形单元离散,其中坝体单元84个,库水声学流体单元33个;流-固耦合界面采用11个两节点界面单元离散;为了同近场库水网格协调,竖直截断边界采用11个两结点线单元离散。材料参数取值如下:坝体混凝土弹性模量Ed=30 GPa,泊松比vd=0.2,质量密度为2 400 kg/m3;库水密度为1 000 kg/m3,动水压力波波速c=1 438.7 m/s。库水表面的压力边界条件为动水压力p=0,库底为刚性库底。
(a)几何模型

(b)有限元网格图3 重力坝-库水系统Fig.3 A gravity dam-reservoir system
为了验证双渐近透射边界单元的正确性及计算精度,采用有限元扩展网格解作为参考解,并与ABAQUS自带的黏性边界模型进行对比。在扩展网格模型中,远场库水有限单元离散长度为3 600 m,动水压力波在该范围内往返传播所需的时间约为5 s(对应的无量纲时间为tc/h=100)。在重力坝基底输入如图4所示的水平向三角脉冲荷载,计算无量纲时间步长取0.1;时步积分算法采用Newmark-β法,积分常数取γ=0.5,β=0.25,即平均常加速度法。高阶双渐近透射边界的渐近阶数取MH=ML=4。
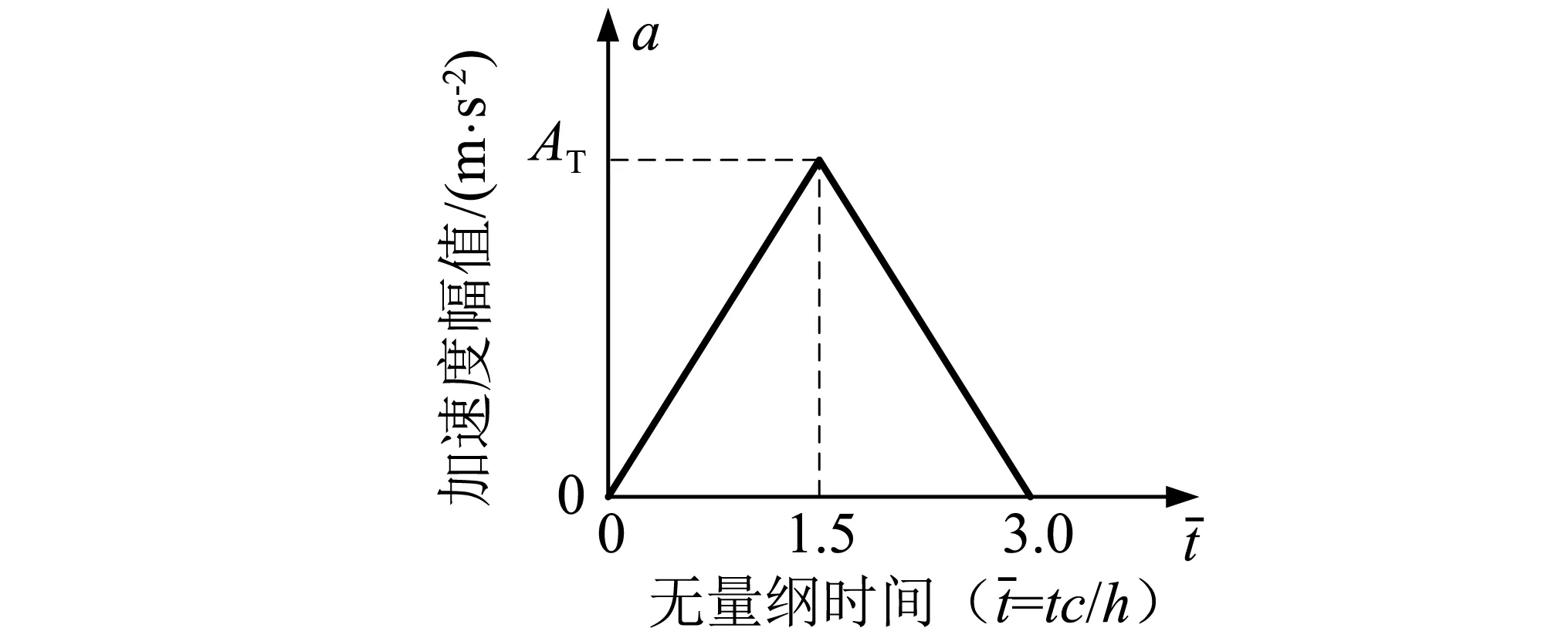
图4 三角脉冲荷载时程曲线Fig.4 Time history of triangular impulse
在水平向三角脉冲荷载作用下,重力坝坝底动水压力时程如图5所示。从图5中可以看出,高阶双渐近透射边界单元(MH=ML=4)的计算结果与有限元扩展网格解几乎完全吻合,而ABAQUS自带黏性边界的计算结果与扩展网格解偏差较大,并且很快衰减到零。因此,双渐近透射边界单元在程序编写上是正确的,并且具有很高的计算精度,在实际应用中可以减小近场库水的离散范围。

图5 三角脉冲荷载作用下重力坝坝底动水压力时程Fig.5 Hydrodynamic pressure responses at heel of the gravity dam subject to triangular impulse
3.2 拱坝算例
考虑图6所示的拱坝-库水系统,混凝土双曲拱坝坝高265 m,水库蓄水深度为252 m,近场库水离散范围约为0.5倍坝高。拱坝和近场库水统一采用8节点六面体单元离散,其中坝体单元6 400个,库水声学流体单元9 792个,流-固耦合界面采用816个4节点四边形单元离散,单元数量为816个;竖直截断边界采用816个4节点四边形单元离散。
计算中,坝体混凝土和库水材料参数、双渐近透射边界单元阶数同重力坝算例,并与自由边界(不考虑截断边界的吸收边界条件)的计算结果进行对比。

图6 拱坝-库水系统Fig.6 An arch dam-reservoir system
考虑拱坝基底受到顺河向(Y向)El Centro地震波作用,其中El Centro地震波的加速度时程曲线参见Wang等的研究。地震波作用下,A点(见图6)的动水压力时程曲线如图7所示。从图中看出,与不考虑辐射阻尼效应的自由边界计算结果相比,考虑了双渐近透射边界后,拱坝坝踵的动水压力响应大大减小了;其中,采用自由边界和双渐近透射边界模型计算,动水压力的峰值分别为3.2 MPa和0.8 MPa。
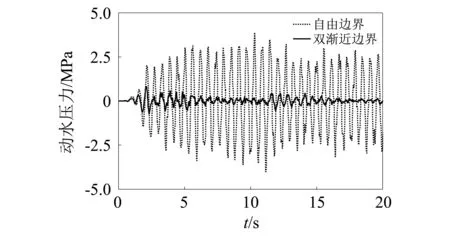
图7 El Centro地震波作用下A点动水压力时程Fig.7 Hydrodynamic pressure responses at point A subject to El Centro earthquake
坝踵动水压力达到峰值时,拱坝上游面的动水压力等值线图如图8所示。从中可以看出,动水压力数值随着库水深度的增加而增大;自由边界模型高估了坝面的动水压力,从而导致拱坝坝体应力的增加,增大了坝体的动力响应。

图8 拱坝上游面最大动水压力等值线图Fig.8 Contour map of the maximum hydrodynamic pressure distribution on the upstream surface of the arch dam
由上述结果可知,采用自由边界模型,即不考虑无限库水的辐射阻尼,在一定程度上夸大了坝面动水压力的数值,由此夸大了坝体的动力响应。无限库水的辐射阻尼效应对坝体动力响应有重要影响,是大坝地震响应分析中应当考虑的重要部分。
4 结 论
高阶双渐近透射边界具有良好的计算精度和计算效率。本文基于ABAQUS提供的UEL接口,采用FORTRAN语言开发了双渐近透射边界单元UEL_DAOB.for,将高阶双渐近透射边界嵌入到ABAQUS,通过算例分析得到以下结论:
(1)重力坝算例验证了双渐近透射边界单元程序的正确性,并且表明高阶双渐近透射边界具有很高的计算精度。
(2)拱坝算例结果表明,与不考虑无限库水辐射阻尼的自由边界计算模型相比,考虑高阶双渐近透射边界后,坝面动水压力大大减小了,其峰值从3.2 MPa减低到了0.8 MPa。
(3)不考虑无限库水辐射阻尼,在一定程度上夸大了坝面动水压力和坝体动力响应,因此在进行大坝动力响应分析时,考虑无限库水的辐射阻尼效应是十分必要的。
本文编写的双渐近透射边界单元用户子程序具有良好的计算精度和适用性,可用于实际大坝的地震响应分析。
