几何画板在立体几何中的应用

刘心玥

【摘要】几何画板是一个动态几何工具，它在数学、物理等领域均有应用，本文针对几何画板在立体几何中的应用进行了具体分析.在概念教学中，它可以使学生对概念的认识更深入;在公式教学中，它可以让学生理解公式的由来从而更好地记忆;在解题中，也可为学生提供一些简便的做题思路，提升解题速度;帮助学生提升直观想象这一数学学科核心素养.

【关键词】几何画板;立体几何;应用

一、引言

我国普通高中数学课程标准指出，我们要更多關注数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等数学学科核心素养的形成和发展，促进学生在不同学习阶段核心素养水平的达成.直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.在传统的教学模式下，基本依赖教师黑板讲解，学生在脑海中构造图像，很不直观.现代教学模式下，更多采用多媒体辅助教学，使教学更直观、生动，也有利于培养直观想象.几何画板这一辅助教学工具至今已成为制作中学数学课件的主要平台之一.

几何画板可以动态的展示相关对象的关系，化抽象为具体、化具体为形象，是21世纪的动态几何.本文我们将着重研究几何画板在立体几何中的应用.作为立体几何初学者，大多数学生缺乏空间想象能力，用几何画板绘制所需的图形，可以使其运动起来，因此，学生得以从多个不同的角度去观察图形，更好地理解和接受立体几何相关知识，提升学生的直观想象能力.接下来，我们将从三个方面来系统阐述几何画板在立体几何中的应用.

二、几何画板在概念教学中的应用

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式，它也是公式、定理和应用的基础.教师需要帮助学生正确理解数学概念，进而灵活运用数学概念.

二面角的大小可以用它的平面角来度量，而二面角的平面角这一概念又较难理解，学生不懂为什么要这么定义，此时我们可以利用几何画板来帮助理解.

首先在画板上做出如下图1所示的二面角α-l-β，射线OA和OB可以分别在半平面α和β内绕棱l上一点O自由旋转，两个半平面α和β也可以以棱l为轴自由转动.当二面角确定时我们应该如何确定二面角的平面角呢？通过转动射线OA和OB，启发学生发现当OA和OB与l所成的角为锐角时，无法准确表达出二面角的大小，只有当OA和OB与l所成的角为直角时才最准确，因此，学生认识到了原来定义是这么来的，概念便在脑海中内化了.转动半平面也可以让二面角的概念进一步深化.

三、几何画板在公式教学中的应用

数学公式是人们在研究自然界物与物之间时发现的一些联系，并通过一定的方式表达出来的一种表达方法.在整个学习过程中，学生需要学习很多公式，但是由于公式非常多，只是死记硬背是不行的，只有知道公式的由来才可以更好地记忆并加以运用.

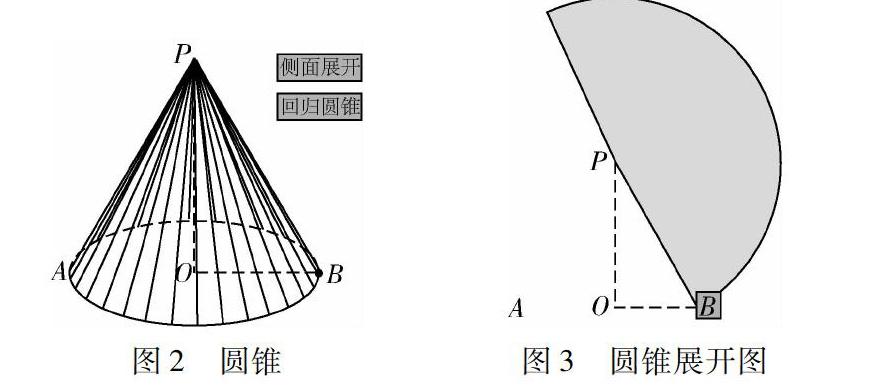
在介绍圆锥的表面积时，书本直接给出了它的侧面展开图和公式，这样学生其实没有理解为什么.通过几何画板先做出圆锥如图2所示，然后利用动画将圆锥展开，如图3所示，则学生可以清楚地看到展开图是一个扇形，因此，面积便可以计算，公式的含义也一目了然.

四、几何画板在解题中的应用

在做题时往往有些较难理解的题目需要解决，而几何画板可以给学生提供另一种思路，方便解题.如2003年的全国高考题：一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为.

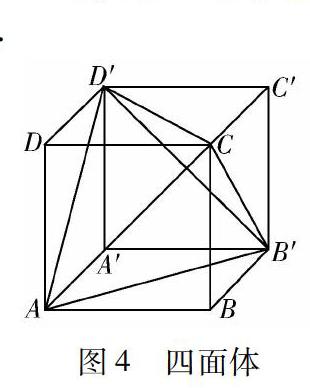
在这道题中，仅仅通过纸和笔或想象并不能想到很好的方法，因此，我们可以用几何画板辅助.由于四面体的所有棱长都为2，而正方体的每个面的每条对角线都相等，因此，我们可以将四面体看为由正方体切割而来，四面体的顶点也就是正方体的顶点.先做出四面体，再将正方体添加上去如图4所示.则四面体C-AB′D′为符合条件的四面体，正方体ABCD-A′B′C′D′的边长为1，四面体的外接球即为正方体的外接球，直径为正方体的对角线长，因此，问题就迎刃而解了.

五、总结

其实几何画板在立体几何中的应用不仅仅体现在上述几个例子中，在其他很多地方都有体现，这里笔者无法将其全部列出.将几何画板应用在立体几何教学中，可以使学生对知识点有更好的理解，它是一个很好的教学工具，为推行素质教育提供了另一个平台.