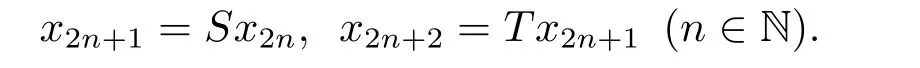一类新型α-可容许映射及相关公共不动点定理

江秉华,蔡择林,李必文,陈金阳

(湖北师范大学数学与统计学院,湖北 黄石435002)

1.引言

2012年,Öztürk等[1]首先介绍了赋值Banach代数的锥度量空间这个概念,他们将赋值Banach代数替换Banach空间并称之为赋值Banach代数的锥度量空间.后来在2013年LIU

等[2]在赋值Banach代数的锥度量空间中给出了几类带有广义Lipschitz常数的压缩映射的不动点定理,并证明了这些定理和其它度量空间中相应结论的不等价性,具有很好的理论和现实意义.后来大量学者把注意力集中在赋值Banach代数的锥度量空间,获得了很多的不动点结论[3−7].

Samet等[8]引入了α-可容许映射,建立了带有α-可容许映射的广义压缩型映射的不动点定理,随后Hussain[9]推广了α-可容许映射并证明了相应的不动点定理,Abdeljawad[10]建立了带有α-可容许映射对的广义压缩型映射的一些不动点定理.Arshad等[11]建立了带有三角型α-可容许映射的广义压缩型的公共不动点定理,更多结果可参考相关文献[12−15].最近,黄华平等[16]建立了带有向量版本的α-可容许映射的广义压缩型不动点定理.这些压缩条件都很弱,使得其应用性大大提高.

本文中,我们首先给出了向量版本的三角型α-可容许映射对的概念,而后建立了相应的Banach型压缩、Kannan型压缩、Chatterjea型压缩的公共不动点定理,因而大大改进了先前的结果.其后,通过实例验证了本文的结论.

定义1.1[2]设A为Banach代数,θ和e分别为A的零元和单位元,P为A中的一个非空的闭子集,R+为非负实数集,若满足：

则称P为A中的一个锥,并称满足条件intP≠ϕ的锥为体锥.这里intP表示P的全体内点所组成的集合.

规定x ≼y ⇔y−x∈P,x ≪y ⇔y−x∈intP,熟知“≼”,“≪”是A中的一个偏序,称“≼”,“≪”为锥P诱导的偏序关系.若存在常数K >0,使得当θ ≼x ≼y时,‖x‖≤K‖y‖(x,y∈A),则锥P称为正规锥,满足前式的最小正常数K称为P的正规常数.

本文中总是假设A为一个Banach代数,P是A中的一个体锥,“≼”,“≪”为锥P诱导的偏序关系.

定义1.2[2]设X为非空集合,A为Banach代数,若映射d:X ×X→A满足：

1)θ ≼d(x,y)(∀x,y∈X),d(x,y)=θ ⇔x=y;

2)d(x,y)=d(y,x)(∀x,y∈X);

3)d(x,y)≼d(x,z)+d(z,y)(∀x,y,z∈X).

则称d为X上的一个锥度量,同时称(X,d)为赋值Banach代数的锥度量空间.

定义1.3[7]设P为Banach代数A中的体锥,{un} ⊂A.若∀c ≫0,总存在一个自然数N,使得当n>N时,都有un ≪c,则称{un}为A的c-序列.

定义1.4[5]设(X,d)为赋值Banach代数的锥度量空间,{xn}⊂X,x∈X.

1) 若{d(xn,x)}为A中的一个c-序列,则称{xn}收敛到x,记为xn→x(n→∞);

2) 若{d(xn,xm)}为A中的一个c-序列,则称{xn}为X中的Cauchy 列;

3) 若X中的每一个Cauchy列都在X中收敛,则称(X,d)是完备的.

定义1.5[8]设X为非空集,α:X×X→[0,∞)为映射,S:X→X是自映射.若∀x,y∈X,α(x,y)≥1⇒α(Sx,Sy)≥1,则称S是α-可容许映射.

定义1.6[10]设X为非空集,α:X × X→[0,∞)为映射.S,T:X→X是自映射,若x,y∈X,α(x,y)≥1⇒α(Sx,Ty)≥1且α(Tx,Sy)≥1,则称(S,T)是X上的α-可容许映射对.

定义1.7[10]设X为非空集,α:X ×X→R为映射,(S,T)是X上的α-可容许映射对.若x,y,z∈X,α(x,z)≥1,α(z,y)≥1⇒α(x,y)≥1,则称(S,T)是X上的三角型α-可容许映射对.

例1.1[11]设X=[0,∞),作映射S:X→X,α:X ×X→[0,∞),使得Sx=2x,

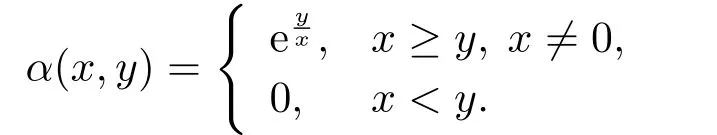
则S是α-可容许映射.

例1.2[11]设X=R,作映射S,T:X→X,α:X×X→[0,∞),使得Sx=2x,Tx=x2,

则(S,T)是X上的三角型α-可容许映射对.

引理1.1[3]设P为Banach代数A中的锥,a,b∈A,c∈P,若a ≼b,则ac ≼bc.

引理1.2[3]设P为Banach代数A中的锥,u,v,w∈P,u ≼v ≪w,则u ≪w.

引理1.3[2]设(X,d)为赋值Banach代数A的锥度量空间,{xn} ⊂X,x,y∈X.若当n→∞时,xn→x,xn→y,则x=y.

引理1.4[4]设P为Banach代数A中的锥,k∈P,{un}为A中的c-序列,则{kun}也为A中的c-序列.

引理1.5[4]设A为带有单位元e的Banach代数,为x∈A的谱半径.若ρ(x)<1,那么e−x可逆,且还有

引理1.6[4]设P为Banach代数A中的锥,k∈P,若ρ(k)<1,则{kn}是一个c-序列.

引理1.7[17]设A为带有单位元e的Banach代数,a,b∈A且a,b可交换,则ρ(a+b)≤ρ(a)+ρ(b),ρ(ab)≤ρ(a)ρ(b).

引理1.8[11]设S,T:X→X是三角型α-可容许映射对.假设存在x0∈X使得α(x0,Sx0)≥1.若x2i+1=Sx2i,x2i+2=Tx2i+1,(i=0,1,2...),则∀m,n∈N,m>n有α(xn,xm)≥1.

2.主要定理及证明

定义2.1设X为非空集,A为带有单位元e的Banach代数,α:X×X→A,S,T:X→X都为映射,满足下列条件：

1) 若x,y∈X,α(x,y)≽e ⇒α(Sx,Ty)≽e且α(Tx,Sy)≽e;

2) 若x,y,z∈X,α(x,z)≽e,α(z,y)≽e ⇒α(x,y)≽e.

则称(S,T)是X上的三角型α-可容许映射对.

定义2.2设X为非空集,A为带有单位元e的Banach代数,α:X ×X→A为映射.若对于满足条件α(xn,xn+1)≽e(n∈N)的{xn} ⊂X,都存在子序列{xni},使得α(xni,x)≽e,则称X是α-弱正则的.

引理2.1设(S,T)是X上的三角型α-可容许映射对,若存在点x0∈X,使得α(x0,Sx0)≽e,定义序列x2i+1=Sx2i,x2i+2=Tx2i+1(i∈N),则∀m,n∈N,m>n有α(xn,xm)≽e成立.

证由x0∈X,有α(x0,Sx0)≽e ⇒α(x0,x1)≽e.因(S,T)是X上的三角型α- 可容许映射对,故α(Sx0,Tx1)≽e ⇒α(x1,x2)≽e ⇒α(Tx1,Sx2)≽e ⇒α(x2,x3)≽e,...,α(xn,xn+1)≽e.再由α(xn,xn+1)≽e,α(xn+1,xn+2)≽e有α(xn,xn+2)≽e.由α(xn,xn+2)≽e,α(xn+2,xn+3)≽e有α(xn,xn+3)≽e....由α(xn,xm−1)≽e,α(xm−1,xm)≽e,即得α(xn,xm)≽e.所以对于∀m,n∈N,m>n有α(xn,xm)≽e成立.

引理2.2设(S,T)是X上的三角型α-可容许映射对,若存在点x0∈X,使得α(Sx0,x0)≽e,定义序列x2i+1=Sx2i,x2i+2=Tx2i+1(i∈N),则∀m,n∈N,m

证类似于引理2.1的证明,即可.

定理2.1设(X,d)为赋值Banach代数A的完备锥度量空间,且A有单位元e.设P为A中的体锥,α:X ×X→A为映射,(S,T)是X上的三角型α-可容许映射对.如果

且满足下列条件:

1) 存在点x0∈X,使得α(x0,Sx0)≽e且α(Sx0,x0)≽e;

2)S和T是连续的或X是α-弱正则的,其中k∈P为广义Lipschitz 常数,且ρ(k)<1,则S,T在X中有公共不动点.

证设x0∈X,取x1∈X,使得x1=Sx0,取x2∈X,使得x2=Tx1.连续这个过程,可以构造序列{xn}⊂X,使得

由假设条件,利用引理2.1 有α(x2n,x2n+1)≽e.由引理1.1 及式(1) 有

再由假设条件,利用引理2.2 有α(x2n+2,x2n+1)≽e.由引理1.1及式(1)有

由式(2)和式(3)有

于是

因此∀m,n∈N,m>n,由引理1.5有

由于ρ(k)<1,由引理1.4 和引理1.6知(e−k)−1knd(x0,x1)是一个c序列.又由引理1.2和式(4)可知d(xn,xm)也是一个c序列,所以{xn}为X中Cauchy列.由于(X,d)的完备性,因此存在x∈X,使得xn→x(n→∞).

如果S,T是连续的,那么

由引理1.3可得Sx=x,Tx=x,即x是S,T的一个公共不动点.

如果X是α-弱正则的,则由假设条件及引理2.1,存在{xni} ⊂{xn},使得α(xni,x)≽e.现在通过式(1) 有

因为{d(x2ni,x)}为c-序列,由引理1.4知{kd(x2ni,x)}也为c-序列.又由引理1.2 知d(x2ni+1,Tx)亦为c序列,从而x2ni+1→Tx(i→∞).再由引理1.3得到Tx=x.类似地,可得Sx=x,因此x=Sx=Tx,即x是S,T的一个公共不动点.

定理2.2设(X,d)为赋值Banach代数A的完备锥度量空间,且A有单位元e.设P为A中的体锥,α:X ×X→A为映射,(S,T)是X上的三角型α-可容许映射对.如果

且满足下列条件:

1) 存在点x0∈X,使得α(x0,Sx0)≽e且α(Sx0,x0)≽e;

2)S和T是连续的或X是α-弱正则的,

其中k∈P为广义Lipschitz常数,且ρ(k)<,则S,T在X中有公共不动点.

证设x0∈X,作点列{xn}⊂X,适合

利用条件α(x0,Sx0)≽e和引理2.1可得α(x2n,x2n+1)≽e,再由条件(5)有

从而

由于ρ(k)<,由引理1.5可得e−k可逆,因而有

令h=(e−k)−1k,注意到ρ(k)<,由引理1.5和引理1.7可得

所以

类似地,有

由式(6)-(7)有

于是

由定理2.1的证明过程知,存在x∈X,使得xn→x(n→∞).

如果S,T是连续的,那么

由引理1.3可得Sx=x,Tx=x,即x是S,T的一个公共不动点.

如果X是α-弱正则的,则由引理2.1及假设条件,存在{xni}⊂{xn},使得α(x2ni,x)≽e.现在通过式(5)有

进而有

注意到(e−k)是可逆的,那么有

因为d(x2ni,x2ni+1)+d(x,x2ni+1)为c-序列,由引理1.4 知(e−k)−1k[d(x2ni,x2ni+1)+d(x,x2ni+1)]也为c-序列,又由引理2 知d(x2ni+1,Tx)亦为c序列,从而x2ni+1→Tx(i→∞).再由引理1.3得到Tx=x.类似地,可得Sx=x,因此x=Sx=Tx,即x是S,T的一个公共不动点.

定理2.3设(X,d)为赋值Banach代数A的完备锥度量空间,且A有单位元e.设P为A中的体锥,α:X ×X→A为映射,(S,T)是X上的三角型α-可容许映射对.如果

且满足下列条件

1) 存在点x0∈X,使得α(x0,Sx0)≽e且α(Sx0,x0)≽e;

2)S和T是连续的或X是α-弱正则的,

其中k∈P为广义Lipschitz常数,且ρ(k)<,则S,T在X中有公共不动点.

证设x0∈X,作点列{xn}⊂X,适合

利用条件α(x0,Sx0)≽e和引理2.1可得α(x2n,x2n+1)≽e.再由条件(8)有

从而

类似地,可得

因此

由定理2.2 的证明过程知,存在x∈X,使得xn→x(n→∞).

若S,T是连续的,则

由引理1.3可得Sx=x,Tx=x,即x是S,T的一个公共不动点.

如果X是α-弱正则的,则由引理2.1及假设条件,存在{xni}⊂{xn},使得α(x2ni,x)≽e.现在通过式(8)有

进而有

注意到(e−k)是可逆的,那么有

因为d(x2ni,x2ni+1)+d(x,x2ni+1)为c-序列,由引理1.4 知(e−k)−1k[d(x2ni,x2ni+1)+d(x,x2ni+1)]也为c-序列,又由引理1.2知d(x2ni+1,Tx)亦为c序列,从而x2ni+1→Tx(i→∞).再由引理1.3得到Tx=x.类似地,可得Sx=x,因此x=Sx=Tx,即x是S,T的一个公共不动点.

注1定理2.1-2.3分别改进了文[2]及文[7]的定理2.1-2.3和定理3.1-3.3的,去掉了文[2]中定理的正规性条件,本文的压缩条件比文[2]及文[9]中的那些定理的压缩条件要宽松得多.

注2在本文定理2.1-2.3中分别假设S=T即可得到文[16]中的定理1-3.