一维光子晶体异质结的界面态研究

郭翊航 赵丽明

(首都师范大学物理系，北京 100048)

0 引 言

光子晶体(又称光子禁带材料)是一种人工材料，由不同介电常数的介质周期排列而成的一种光学结构[1]．类比于半导体晶体对电子输运行为的影响，光子晶体具有光子的带结构，原则上可以通过设计和制造光子晶体及其器件达到控制光子运动的目的[2-3]．光子晶体的出现，使操纵和控制光子的梦想成为可能．

按照空间维数的划分，光子晶体可以分为一维光子晶体、二维光子晶体和三维光子晶体，其中一维光子晶体的色散关系可以得出确切的解析解，并且其结构简单，易于实现[4]．在光子晶体的能带图中，如果两条能带交于一点，在该点附近，其色散关系呈线性关系时，该交点就称为光子晶体的狄拉克点．狄拉克点的形成主要是由结构的对称性产生的，在电子晶体比如石墨烯的高对称点处就会由于结构存在必然简并狄拉克点，或者是由于能带特性存在偶然简并狄拉克点．而电子狄拉克点所表现出的许多有趣的性质，比如赝散射、拓扑传输、界面态、震颤等现象在光子晶体中也被广泛地研究[5-11]．和电子晶体狄拉克点不同的是，光子晶体的狄拉克点现象更易观察，因为光子不会和介质本身产生相互作用，还可以通过超材料技术对光子晶体做更细致地修改，比如折射率调节、形状调节、角度调节、缺陷制造等[12-15]．这些都可以增进对于光子晶体狄拉克点的控制．

通过狄拉克点很容易找到界面态．具体方法为：分别从不同方向调节体系的参数，改变结构的介电常数和尺寸，可形成2个不同的光子晶体．这2个光子晶体在狄拉克点附近具有共同的带隙，但具有不同的拓扑相位，当将这2个光子晶体拼接在一起时，会出现界面态，该方法被称为狄拉克点方法[16]．研究发现：界面模的能级满足简单的正弦函数关系[4]．然而一些问题还未澄清：利用狄拉克点方法，在什么样的范围内界面模一定存在；是否有最佳的界面模匹配条件能够使得界面模的折射率达到完全透射等．本文主要通过对一维光子晶体异质结折射率的调制，得到存在界面模的极限参数，并且得到界面模峰值的最佳匹配条件．这一发现将对实际应用有潜在的指导意义．

1 数值模拟与讨论

假定体系由一维多层介质组成，介质的总层数为N．对于第L层，电场满足如下形式：

(1)

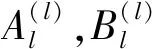
(2)

可以得到：

(3)

其中：

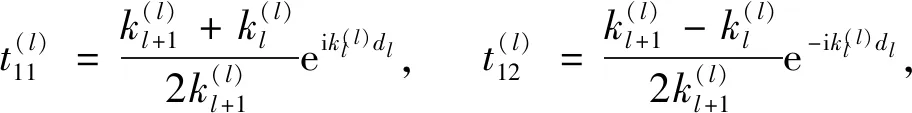
(4)

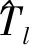
(5)

由于BN=0，因此

(6)

相应的透射率为：

(7)

反射率为：

(8)

通过公式(5)、(7)和(8)可以计算出在一维介质层体系中电磁波的电场和磁场以及透过率，反射率等物理量．

假定一维光子晶体是由2种不同的材料(AB)组成，其中介质A的折射率和厚度分别用na，da，介质B的折射率和厚度分别为nb，db．光子晶体的层数为m(本实验中m=8)．对于完美的光子晶体，其色散关系满足如下关系:

(9)

其中q为布洛赫波矢，Λ为晶格常数，这里假定晶格常数为 1．根据文献[6]，当归一化频率满足如下关系：sinkada=0，sinkbdb=0，sin(kada+kbdb)=0，该频率为狄拉克点．本文选择文献[5]的参数(na=2,nb=1，da=0.4，db=1-da=0.6)．图1给出了该结构下的色散关系，可以发现在ω=2.5处出现狄拉克点．对于该结构，周期单元的光程为L=nada+nbdb，定义光程常数L0，使得L0=L．本文以下提到的光程常数均指L0．

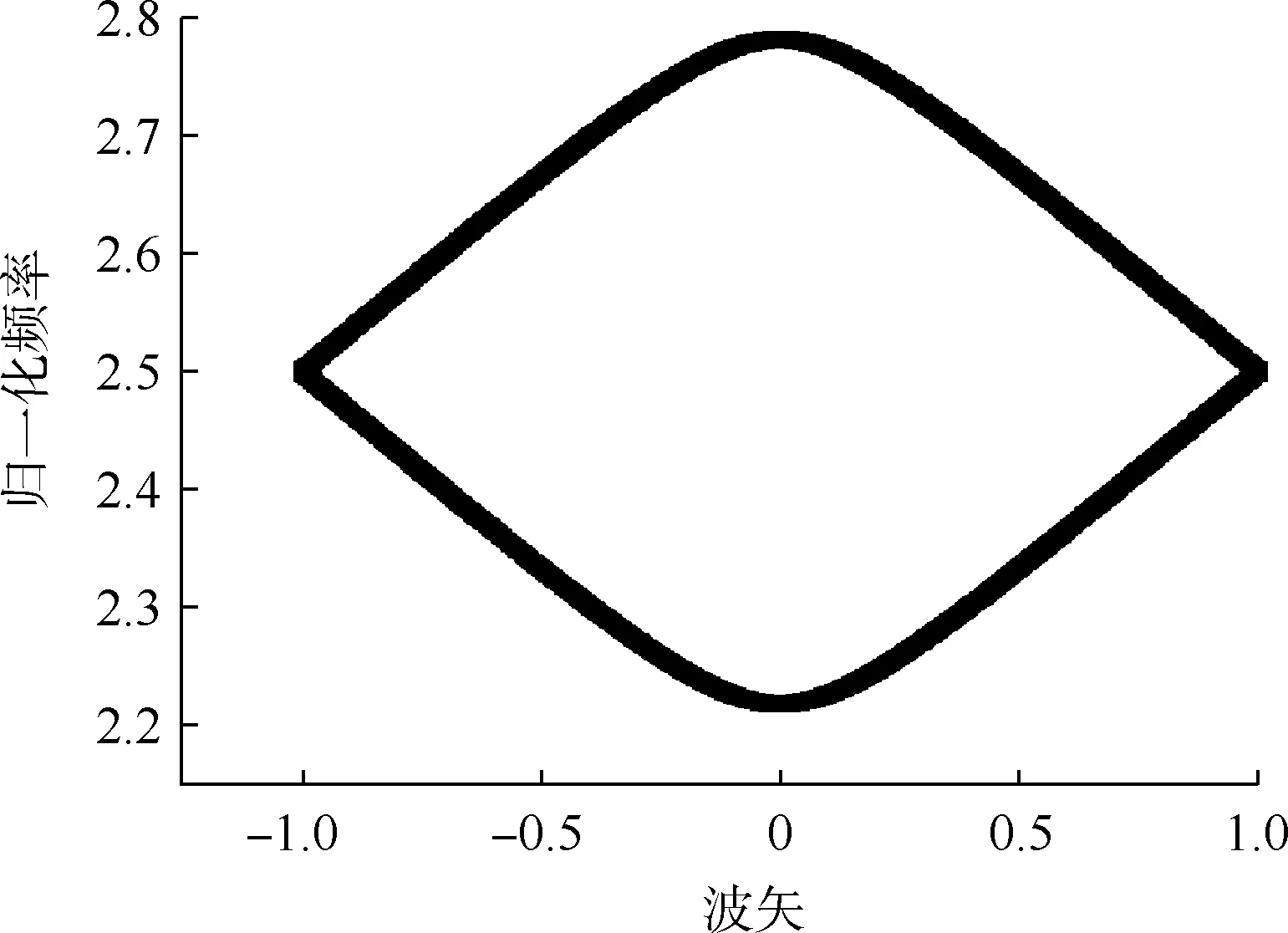
图1 一维光子晶体(AB)m在狄拉克点处的能带关系

现在可以分别沿不同方向调节体系的参数，可形成2个不同的光子晶体(AB)m和(CD)m，并且要求这2个光子晶体的周期单元光程均等于L0．PC1使用如下参数，da=0.42,db=0.58．εa=3.8，εb=1.PC2的参数则为dc=0.38,dd=0.62．εc=4.2，εd=1．图2分别给出了PC1和PC2的色散关系，结果表明当这2个光子晶体的周期单元光程相等时，发现狄拉克点张开，且在狄拉克点附近具有共同的带隙，但具有不同的拓扑相位．如果将这2个光子晶体拼接在一起时，只要带隙中存在某一个频率能够与结构发生共振，则会产生界面模．界面模的消失主要由2种原因：(1)界面模的归一化频率超出了带隙范围；(2)光子晶体参数的改变使得拓扑相位发生了反转．

下面将这2个不同的光子晶体拼成异质结结构：(AB)m(CD)m，如图3所示．图4给出了(AB)m(CD)m的透过率曲线，可以发现在归一化频率ω=2.45处出现界面态，其透过率为0.8．现在想了解的问题是：(1)结构参数变化到何种程度，界面态消失？(2)是否所有界面模都有高的透过率，若不是，是否存在最优的界面模匹配条件？

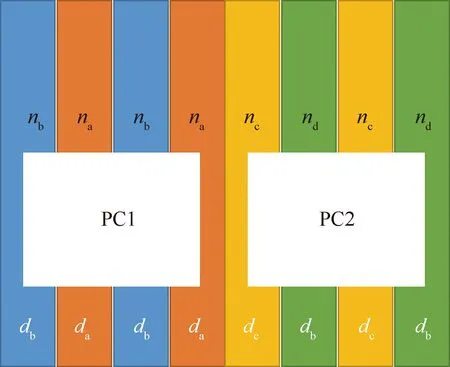
图3 一维光子晶体异质结(AB)m(CD)m的结构示意图

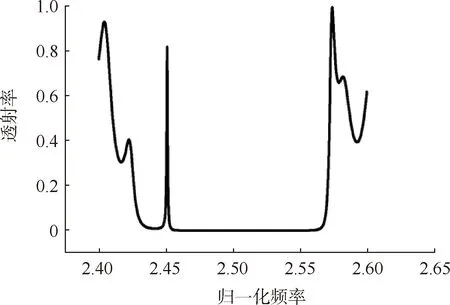
图4 (AB)m(CD)m透射率随频率的变化关系

图5给出了不同δa下透过率随频率的变化关系．可以发现，峰值对应的频率为相应的界面模频率．当δa较小时，界面模的透过率很高，随着δa增大，界面模的透过率显著降低，而δa为14%时，界面模的透射完全消失．本文计算了其他偏移率的透过率曲线，发现δa在小于14%的范围内均可以发现界面模，而超过14%界面模消失．因此在狄拉克点附近存在界面态有一定的范围限制．

下面讨论δa≠-δc的情况．假定PC1的结构固定，其参数为na=1.85,da=0.470 6，通过改变PC2的折射率nc，根据公式(2)得到相应的dc，因此仅通过改变nc，PC2的结构就可以固定．图6描述了界面模的透过率随nc的变化，发现当nc=2.17时界面模的透过率为1，偏离2.17时界面模的透过率减小．这说明na=1.85时，其最佳匹配结构相应于nc=2.17.图7给出了不同的na下界面模透过率随nc的变化曲线．发现他们曲线形状基本类似．不同的PC1都有相应最佳匹配的PC2．

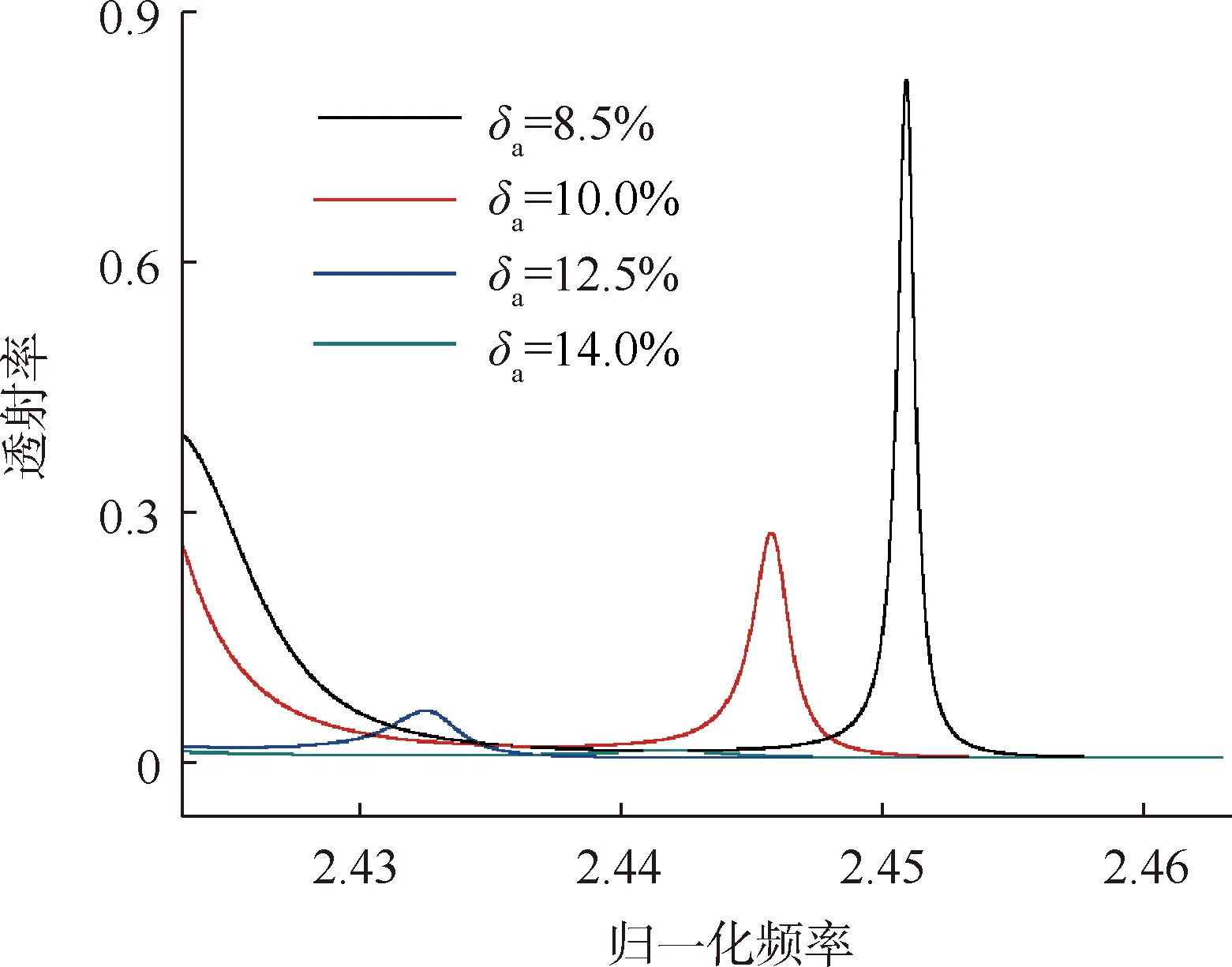
图5 界面模透射率随归一化频率变化图像

固定PC1参数nada，nbdb，随着PC2折射率的改变，整体异质结构的界面模透射率和界面模位置都有不断的变化．可以基本掌握每一组PC1的偏移率参数所对应的完全透射的界面模位置，总结为表1．

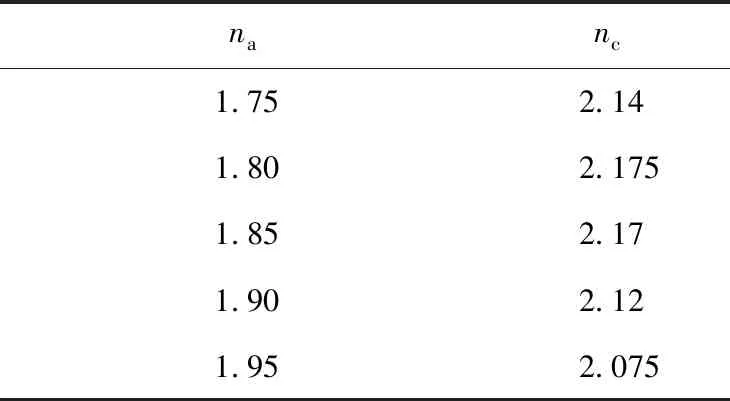
表1 透射率最佳时的一维光子晶体异质结构参数

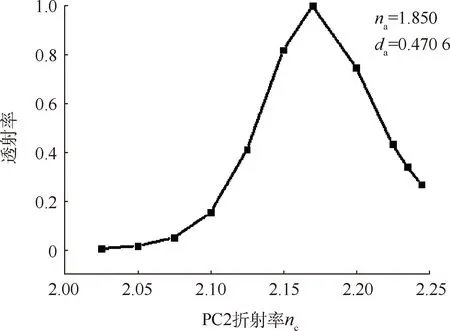
图6 不同的异质结构下，界面模的透射率随PC2折射率nc的变化曲线

表1给出了PC1所对应的最佳匹配的PC2，特别强调的是PC1的结构仅由na决定，PC2的折射率仅由nc决定．还可以给出很多这样的匹配的光子晶体异质结结构，使得界面模的透过率为1．

2 总 结

本文采用狄拉克点方法研究光子晶体异质结的界面态．通过调节体系的参数，研究了偏移率对光子晶体异质结构界面态的透过率影响，并且进一步探讨了存在界面态的极限条件．研究了存在界面态的范围内满足对称条件下的异质结界面态的透射率随光子晶体折射率的变化关系，发现每一个PC1都有最佳的PC2与之匹配，使得界面模透过率为1．

图7 PC1介质折射率参数na取不同值时透射率随PC2折射率nc的变化曲线