基于决策树的存量客户流失预警模型*
2019-10-16赵娟娟贾郭军
杨 荣 赵娟娟 贾郭军
(山西师范大学数学与计算机科学学院,山西 临汾 044600)
0 引 言
随着全业务运营,各运营商之间的竞争日趋激烈,电信行业的传统业务面临巨大的压力.因此,各运营商都加大了在存量市场的争夺,对于不同业务的后进入者,市场竞争往往选择跟随策略,竞争目标多为存量市场,导致客户在各运营商之间的流转加快,各运营商拆机率均居高不下.与此同时,存量流失造成用户发展效率低,资源消耗严重,损害了企业价值,存量下滑成为公司发展的重要风险.因此,实现存量用户基本稳定、提升客户忠诚度,提升客户价值已成为各大运营商的经营理念之一.有效降低存量客户的流失率才能固其根本.
为加强针对存量经营工作的大数据支撑能力,形成以客户为中心的管理运营模式,就需以存量客户为切入点,并建立存量客户流失预警模型,通过加强对高流失概率的用户进行提前预警维系,以达到存量客户保有率的提升效果.
1 国内外研究现状
客户流失预警模型的应用研究如今已非常广泛,常用算法包含神经网络、决策树、随机森林等.李爱民[1]采用K-means聚类分析和Logistic回归建立客户流失预警模型相结合的算法来分析各种因素对客户流失的影响程度.周静等[2]构建了计量经济模型,并研究了公司保留策略与延长客户生命周期之间的相关性;陈纪铭[3]使用朴素贝叶斯算法建立了学员流失预警模型,但该模型假设属性之间相互独立,但在实际使用中属性个数比较多或者属性之间相关性较大时效果较差.林明辉[4]利用神经网络的自适应算法,将代表离网用户行为特征的45个指标进行样本训练,最终得到客户流失行为倾向的判断模型;Huang和He[5]提出了优化PSO算法和BP神经网络算法相结合的方法来建立企业客户流失预警模型,但神经网络模型需要大量的参数,且黑盒操作,不能观察之间的学习过程,输出结果难以解释,会影响到结果的可信度和可接受程度;同时大多数公司都使用建模工具来直接建立流失预警机制,准确率仍然较低,本文使用python环境进行建模,并使用决策树模型,并对模型进行优化,使模型算法结果的预测准确率更高.
2 相关算法介绍及算法实现
2.1 CART算法概述
本文使用的是决策树中的CART算法,决策树学习一般分为三个步骤,即特征的选择、决策树的建立、决策树的剪枝;该算法是一种二叉树形式的决策树算法,其中,二叉树算法只把每个非叶节点引申为两个分支,首先进行二元分割,将样本数据划分成两个子集,其次对子集再分割,自顶向下不断递归生成树,直至分支差异结果不再显著下降,即分支没有意义,决策树建立完成[6].因此确定分枝标准是CART算法的核心,从众多分组变量中找到最佳分割点,本文通过 Gini 指标来衡量数据纯度.
2.2 Gini系数
假设样本数据分为K类,其中样本点属于第k类的概率为pk,则概率分布的基尼指数定义为:
(1)
对于二分类问题,若样本点属于第1个类的概率是p,则概率分布的基尼指数为
Gini(p)=2p(1-p).
对于给定的样本集合D,其基尼指数为
(2)
这里,Ck是D中属于第k类的样本子集,K是类的个数.
如果样本集合D根据特征A是否取某一可能值a被分割为D1和D2两部分,即
D1={(x,y)∈D|A(x)=a},D2=1-D1.
(3)
则在特征A的条件下,集合D的基尼指数定义为
(4)
基尼系数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性,基尼指数越大,样本集合的不确定性也就越大.
2.3 决策树建立
输入:训练数据集D,停止计算的条件
输出:CART决策树
根据训练数据集,从根结点开始,递归地对每个结点进行以下操作,构建二叉决策树:
(1)设结点的训练数据集为D,计算现有特征对该数据集的基尼指数.此时,对每一特征A,对其可能取的每个值a,根据样本点对A=a的测试为“是”或“否”分割为D1和D2两部分,利用式(4)计算A=a时的基尼指数.
(2)在所有可能的特征A以及他们所有可能的切分点a中,选择基尼系数最小的特征及其对应的切分点作为最优特征与最优切分点.依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中去.
(3)对两个子结点递归地调用(1)和(2),直至满足停止条件
(4)生成CART决策树
2.4 决策树剪枝
算法过程如下:
输入: CART算法生成的决策树T0
输出: 最优决策树Tα
1)初始化αmin=∞, 最优子树集合ω={T};
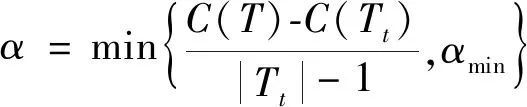
3)得到所有节点的α值的集合M;
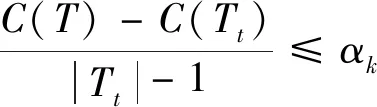
5)最优子树集合ω=ω∪Tkω,M=M-{αk};
6)如果M不为空,则回到步骤4.否则就已经得到了所有的可选最优子树集合ω;
7)采用交叉验证在ω中选择最优子树Tα.
3 实验过程
3.1 数据处理及分析
(1)数据定义
数据表中共包含十个字段,如表1所示,表中部分数据如表2所示:
(2)缺失值处理及变量筛选
处理过程中未发现缺失值且未出现重复ID,因此可直接进行变量筛选.
分析发现已流失客户的使用月数均小于25,因此判定该字段并不关键,选择以下字段作为特征变量extra_time,extra_flow,pack_type, pack_change, asso_pur、contract以及group_use,并将连续变量转换为二分类变量,将没有超出套餐的通话时间和流量记为0,超出的记为1.转换后部分数据如表3所示:

表1 相关字段及定义
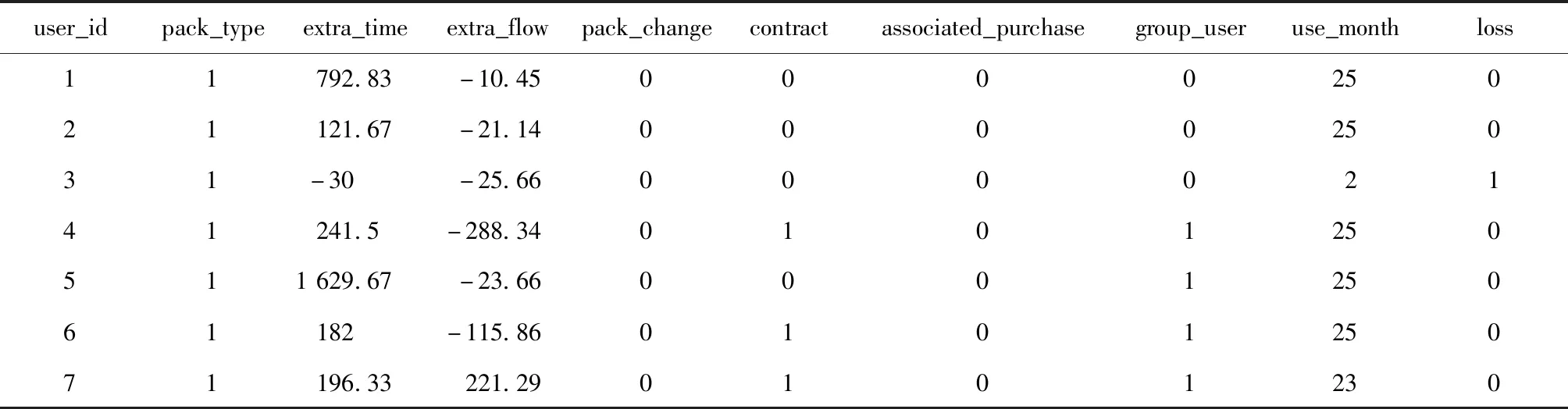
表2 表中部分数据展示
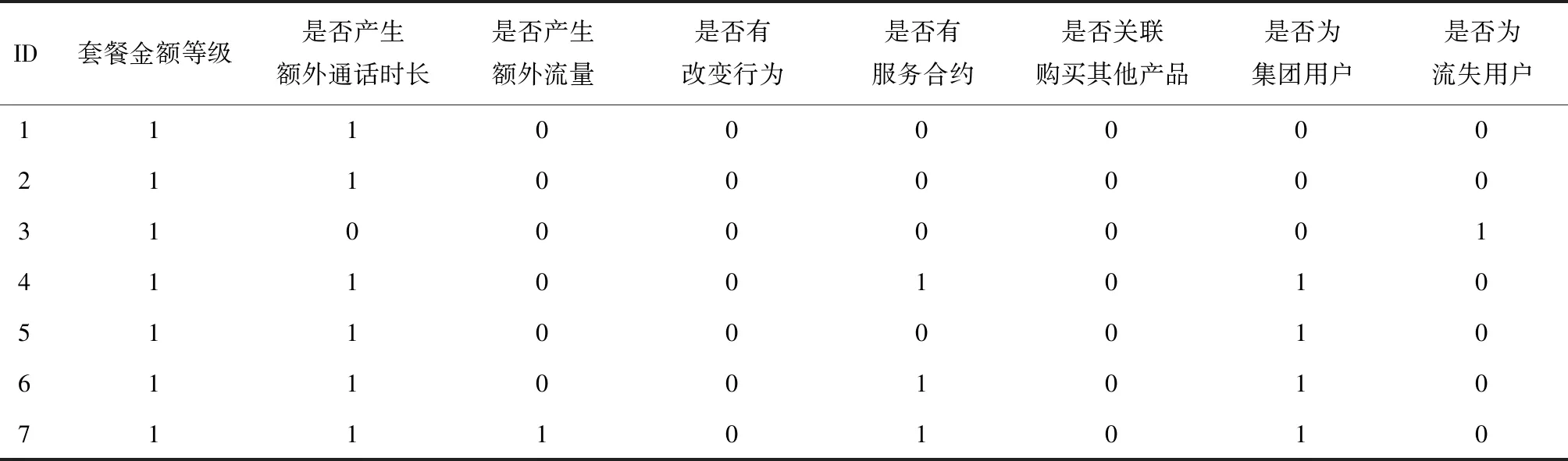
表3 表中部分数据展示(处理后)
(3)相关性分析
通过相关性矩阵热力图观察各变量之间的相关性,可发现各属性间相关性较低.
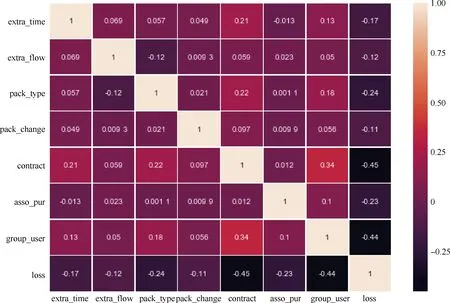
图1 相关性矩阵热力图
3.2 建模过程
(1)建立自变量x,因变量y的二维数组;
(2)以7∶3的比例拆分训练集及测试集;
(3)使用CART算法建立决策树模型并拟合训练,基于Gini系数进行分类,设置树的最大深度为6,区分一个内部节点需要的最少的样本数为9,一个叶节点所需要的最小样本数为5;
(4)模型评分值对比
针对测试集和训练集分别进行评分,如表4,得知测试集和训练集评分值较接近,模型效果较好.

表4 评分值对比
3.3 模型优化
对于决策树来说,可调参数有
max_depth:限定了决策树的最大深度,可有效防止过拟合;
min_samples_leaf:限定了叶子节点包含的最小样本数,该属性可有效防止数据碎片问题;
min_samples_split:分裂所需最小样本数;
min_impurity_split:该值限制了决策树的增长,若某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值,则该节点不再生成子节点.
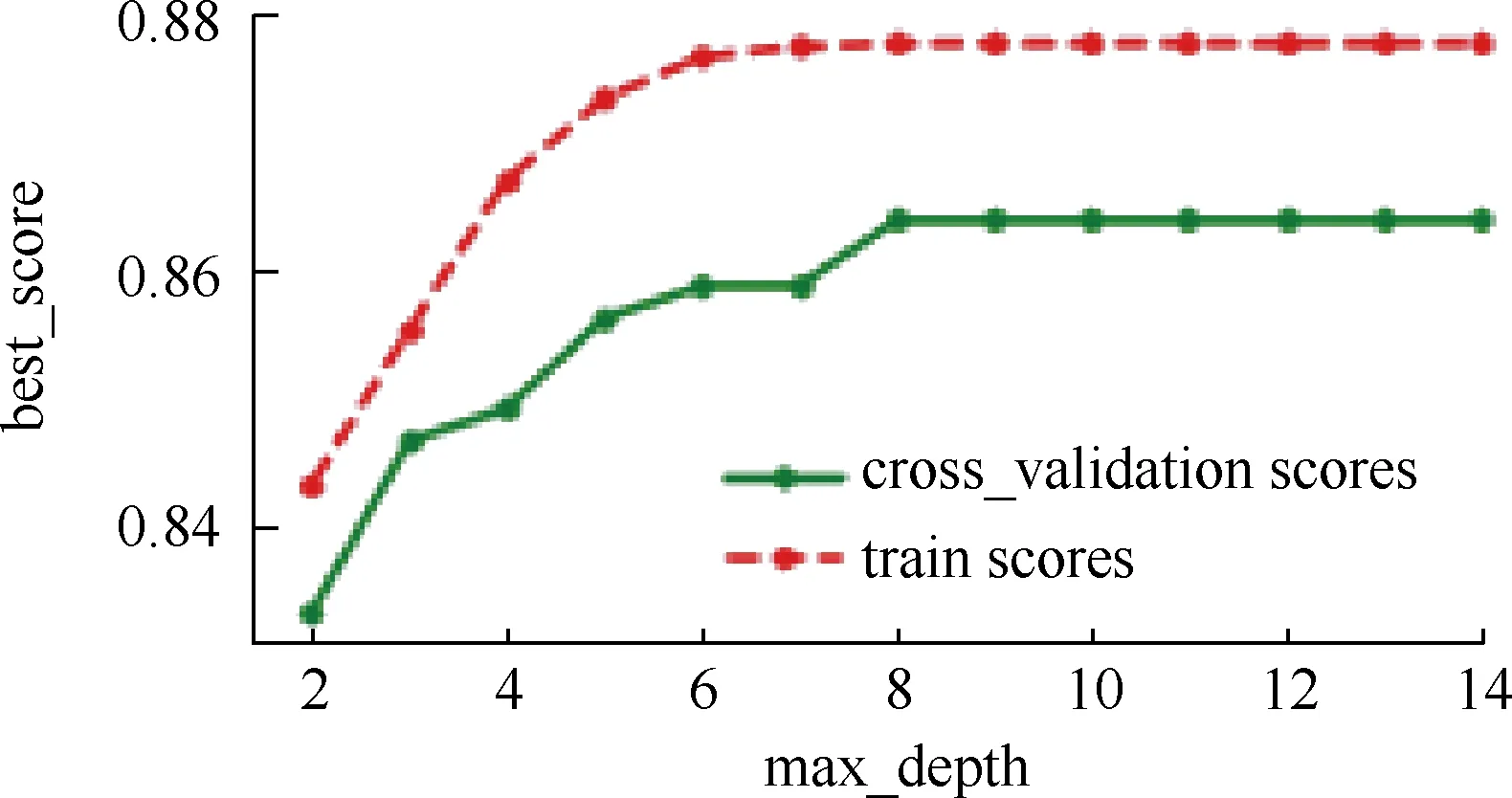
图2 模型参数与评分效果的关系
由于本文训练数据有限,易出现过拟合现象,故期望能通过调整参数来有效防止过拟合.本文选择对max_depth进行调整,缓慢增加深度来对模型进行训练,并计算评分数据,利用交叉验证法找出评分最高的索引.同时输出模型参数与评分效果的关系图及最优参数值,如图2所示,优化后评分值对比如表5所示.

表5 评分值对比(调参后)
3.4 模型评估及可视化结果
输出决策树模型评价结果,如表6所示.可得出建立的预测模型的精确率为0.86,说明在预测为流失的用户中,实际流失的用户占86%;同时召回率也为0.86,说明实际为流失的用户中,预测为流失的占86%,F1值为0.86.使用逻辑回归算法预测模型精确率为0.83,预测精度较低,且逻辑回归算法易欠拟合,对比可得出决策树模型算法的综合效果较优.输出决策树模型的roc曲线图,如图3所示,可得auc值为0.73,模型还有待优化.同时输出决策树结构图,如图4所示,部分决策树详情可见图5.
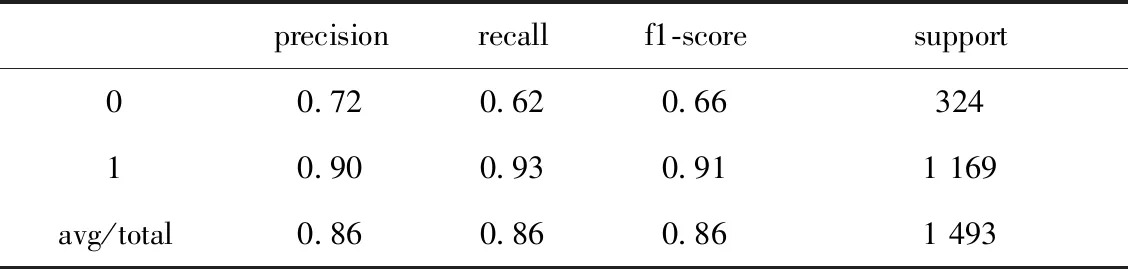
表6 模型评价结果对比
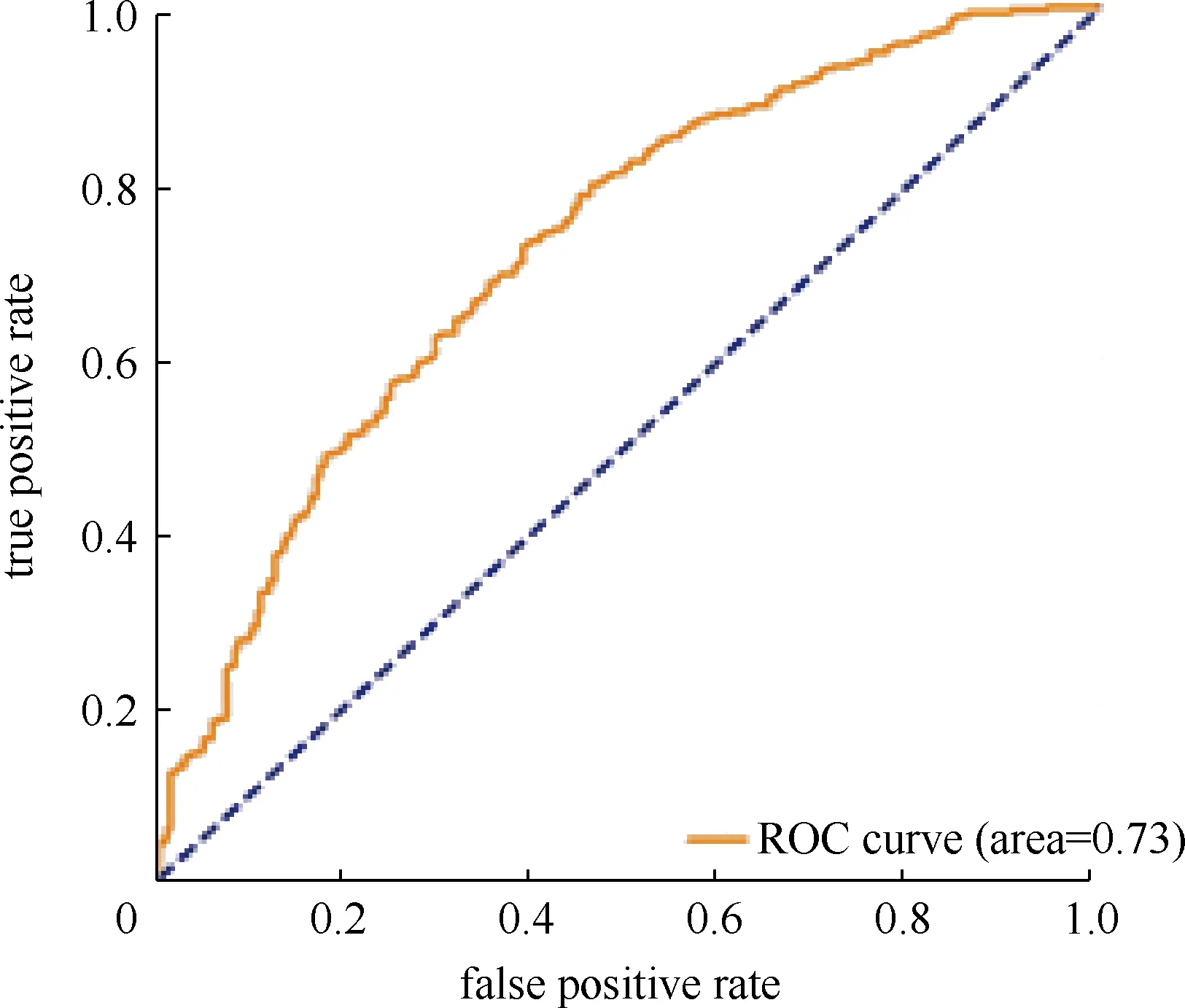
图3 roc曲线图
图4 决策树结构图
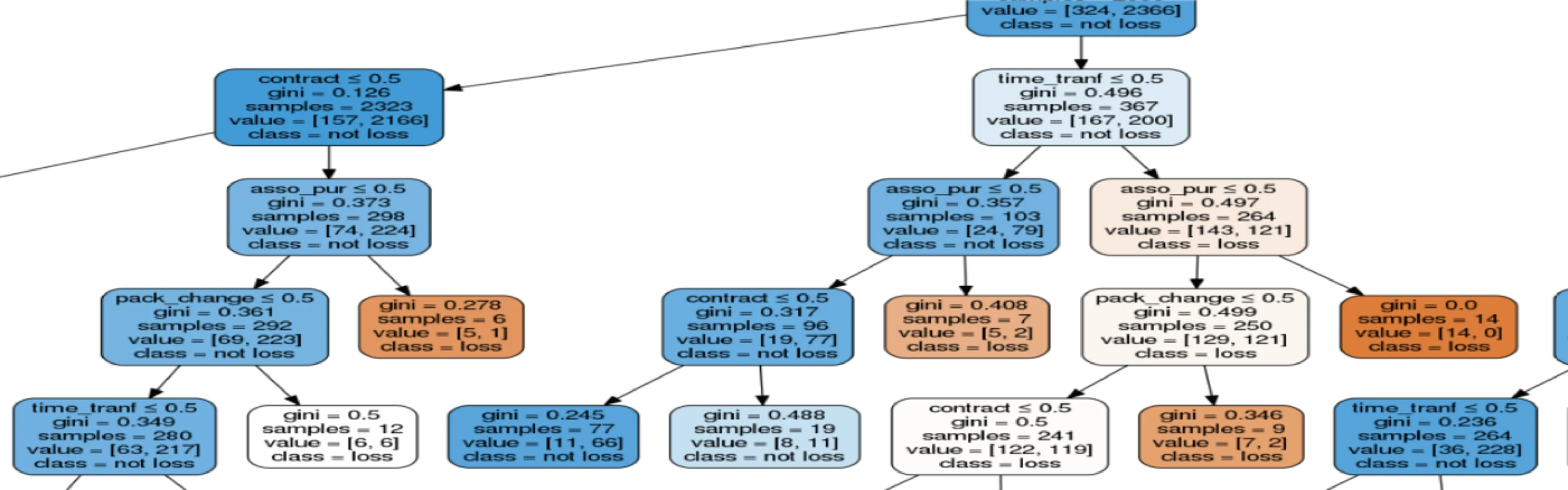
图5 决策树部分分支展示
4 总 结
本文通过决策树中的CART算法成功预测到即将流失的客户,预测成功率达到0.86,与逻辑回归算法相较更优,且AUC达0.73,证明模型效果较好;但实际应用中要尽可能的找全部实际将流失的用户,即实际流失的用户中,模型能准确预测到的客户规模.
在今后预测模型的优化上,还有很多的改进之处,如调整决策树的参数,特征的精细化筛选,或采用随机森林、遗传算法多算法相结合的方式进行模型评估,并分析用户分类、生命周期以及各变量之间的交叉性和相关性等等,以达到更好的预测效果.
