基于多重多元回归的多目标影响因素效应比较及应用——以企业经营活动分析为例

耿修林，黄婷婷

(南京大学 a.商学院；b.数学系，江苏 南京 210093)

一、引言

作为营利性组织的企业，在日常经营管理活动中其追求的运营结果往往表现在多个方面。有投入才会有产出，企业经营发展获得的产出效果，与企业所投入的资源存在密不可分的关系。企业投入的各项资源，按其功能或管理需要可以将它们区分成不同的类别，比如：反映用工方面投入的资源，反映资金方面投入的资源，反映企业生产和产品技术方面的投入，反映运营管理活动方面投入的资源等。选取什么样的解释变量来说明被解释变量，有各种各样的方法，但从服务于管理决策的目的出发，依据在与目标变量之间存在客观关系的一系列管理手段或措施中确定解释变量，不失为一种效率较高且针对性更强的做法。

管理活动的重要任务之一是对企业运行目标的管理，任何管理目标的实现都依赖于资源投入和借助于合适的管理手段或措施。如果把管理目标或运营管理活动所形成的结果当成被解释变量，那么相应投入的管理资源或采取的管理手段就可当作解释变量。实现管理活动的目标或获得管理活动的结果，可能存在各种各样资源投入方案，也可能存在各种各样的管理手段和措施，问题是怎样才能找到那些富有效率的管理资源投入方案、管理手段或措施。解决这一议题，需要分析管理目标变量和管理手段变量之间的关系，以期能把那些对管理目标起着重要影响作用的管理手段、措施或资源投入方案区分出来，只有这样，管理人员才能有目的地采取相应的管理手段、措施，以及筹划好资源利用方案。衡量手段变量与结果变量之间关系的方法有很多，如投入产出法、EDA分析法等[1-13]，但运用相关回归分析模型始终是极为普遍的做法而且容易实现。

对只有一个管理目标和一个管理手段，要想判断管理手段对管理目标的影响效应，也许通过建立简单回归分析模型就能说明问题。对单一管理目标和多个管理手段，要想分析某个管理手段对管理目标的影响是否存在，运用多元回归分析模型也很容易实现，这时只要检验该解释变量的回归系数是否显著不等于零即可。比较两个不同的管理手段或部分管理手段与另一部分管理手段，对单个管理目标的综合影响效应是否存在差异及其大小，利用一般的多元回归模型也能达到目的。这里有必要指出，许多实证分析的研究论文中，经常不自觉地直接根据估计出来的回归方程中解释变量系数值的大小，来反映解释变量对被解释变量的作用程度，如此做法可能存在以下问题：1.把解释变量的回归系数直接当成该解释变量对被解释变量的影响效应，甚至进行相互间的大小比较，这种做法可能不合适，理由是在有多个解释变量的回归分析中，某个解释变量的回归系数会受到其他解释变量的影响，也就是说该解释变量的回归系数除了自身对被解释变量的影响外，还掺杂着其他解释变量通过该解释变量产生的对被解释变量的影响，至于怎么解决这个问题可参见Weisberg S所著的《应用线性回归》(王静龙、梁小筠、李宝慧译)[14]；2.把解释变量的回归系数当成是该解释变量对被解释变量的影响效应(比如：边际溢出效应，弹性贡献)情有可原，但在含有多个解释变量的多元回归分析中，用两个解释变量回归系数值比较它们对被解释变量的影响效应大小，可能就不符合统计推断原理要求了，原因是依据样本数据进行的相关回归分析，对其结论仍然需要诉诸于统计假设检验，可是在一些回归分析实证文章中没能给予足够的关注，相反却在用样本资料求得回归系数值后把它们当成确定性数值进行大小比较。样本是随机变化的，因此依据样本信息得到的样本统计量值也会随之变化，这样在对比统计量值之间大小的时候，就必须要诉诸于统计推断的手段。

本文侧重于多个被解释变量和多个解释变量回归(Multivariate Line Regression，多重多元回归，俗称“多对多回归”)效应比较。这样做的理论价值和实际应用意义在于：首先多对多回归不仅仅是一般多元回归的简单拓展，由于多个被解释变量之间可能存在相关关系，因此多重多元回归时的方差估计以及由此而来的检验统计量构造，与一般的多元回归分析存在一定的差别；其次，多重多元回归效应比较的内容更为丰富，包括不同解释变量组合间对同一被解释变量影响效应的差异比较、同一组解释变量对不同被解释变量影响效应的差异比较、不同解释变量组合间对所有被解释变量的影响效应比较等。从定量角度测算这些解释变量对被解释变量的影响效应的差异，或许能帮助企业更合理地进行资源利用决策。

二、回归效应比较原理

从形式上看，在多个解释变量与多个被解释变量之间建立回归分析，似乎是多元线性回归模型的自然延伸，但做这样的拓展是有价值的。一个被解释变量会受到众多因素的影响，反过来这些因素也会产生多个影响结果。

假定有k个解释变量x1，x2，...，xk，p个被解释变量y1，y2，…，yp，采集到n组观察资料(yi1，yi2，…，yip；xi1，xi2，…，xik)，i=1，2，…，n，在对x1，x2，…，xk和y1，y2，…，yp中每个变量各自进行标准化处理后，多重多元回归模型可以表示为：

Y=Xβ+ε

(1)

式(1)中

另外，假定ε(i)=(εi1，εi2，…，εip)′(i=1，2，…，n)相互独立，且服从均值0、等协方差Σ=(σij)(j=1，2，…，p)p维正态分布。式(1)回归参数的估计量为[15-16]：

(2)

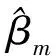
(3)

(4)

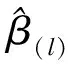
(5)

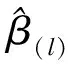
(6)

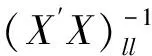
(一)两组不同解释变量对某个被解释变量回归效应的比较

假定两组解释变量为：x1，x2，…，xm1；xm1+1，xm1+2，…，xm1+m2。被解释变量yi，i=1，2，…，p。考虑检验的假设：

H0i：β1i+β2i+…+βmi=βm1+1i+βm1+2i+…+βm1+m2i，i=1，2，…，p

(7)

记ei=(0，0，…，0，1，0，0，…，0)′为第i个分量为1，其余为0的p维列向量，c=(1，1，…，1，-1，-1，…，-1，0，0，…，0)′为k维列向量，则式(7)可以表达为：

H0i～c′βei=0，i=1，2，…，p

(8)

由于

(9)

而

(10)

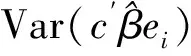
(11)

因此得：

(12)

又因为

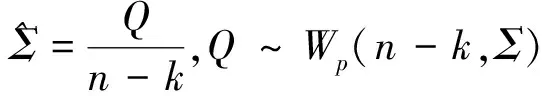
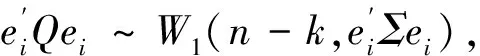
于是得到检验统计量：

(13)

(二)同一组解释变量对不同被解释变量回归效应的比较

假设该组含有m1个解释变量，比较其对被解释变量yi，yj(i≠j，j=1，2，…，p)的影响效应。以双边假设检验为例，原假设和备择假设可以表示为：

H0：β1i+…+βm1i=β1j+…+βm1j

H1：β1i+…+βm1i≠β1j+…+βm1j，

i≠j=1，2，…，p

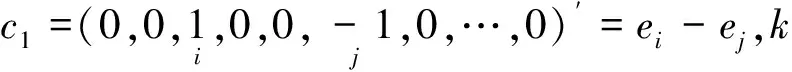
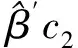
(14)

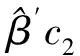
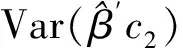
所以存在

(15)

并且

(16)

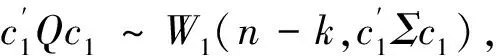
当原假设成立时，检验统计量：

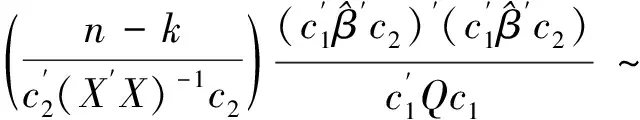
F(1，n-k)

(17)

(三)两组不同解释变量对所有被解释变量回归效应的比较

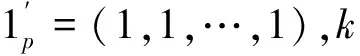
因此，检验统计量的抽样分布：

(18)

三、应用实例与说明

本文这一部分的目的在于对上述所讨论的多重多元回归效应的比较方法做出应用说明，所以可能与专业性质的逻辑分析或一般的实证分析存在差别。习惯意义上的实证分析，原则上以理论为指导、以定性分析为先导，然后诉诸于数据分析佐证，但本文不以获得政策建议为主要目的，只是验证上述方法的可行性。

(一)数据来源与变量界定

1.数据来源

实证分析依据的数据来自于国泰安(CSMAR)数据库。首先从该数据库导出了2011—2016年沪深交易所挂牌交易的2 260家制造业上市公司的年报资料，然后剔除ST、*ST类企业，以及年报资料缺失较多不适宜做回归分析的企业共计890家，最终纳入数据分析对象的企业计有1 369家。在这些企业中，有的有6年完整的年报资料，有的只有1、2年数据。不平衡面板数据的多重多元回归问题有待于进一步研究，这里为“突出”多重多元回归影响效应的比较，对拟定的回归分析变量(包括解释变量和被解释变量)，取1 369家企业2011—2016期间各自相应的代表性数值，主要是对每家企业拟定分析变量的时间序列做均值处理，在此基础上再对每个变量的1 369项数据实施标准化。

2.变量界定

被解释变量。企业经营管理活动的结果表现在各个方面，并且也会随着企业经营管理的内外环境的变化不断改变，但维护和增强企业的经营能力始终是重要的议题。这里采用企业的盈利能力和发展能力作为被解释变量。无论是企业盈利能力还是企业发展能力，不是用某一个指标就能说明的，相反需要设置一系列指标共同结合起来反映。根据财务管理学原理，企业的盈利能力可以用总资产报酬率(ROA)、净资产收益率、营收利润率(利润/营业收入)、每股收益率等指标来表征。企业发展能力是企业经营发展的潜能或可能存在的趋势状态，可以采用的表征指标：总资产增长率、净资产增长率、营业利润增长率、营业收入增长率等。作为一个应用实例，为简化起见(主要是减少被解释变量的数目)，本文根据采集的样本数据先对企业盈利能力和企业发展能力的各个表征指标在1 369家观察企业中进行主成分分析，在得到各项指标的载荷系数后以其为权重，对每个企业的盈利能力、发展能力的表征指标进行加权综合处理，以获得各个企业的盈利能力和发展能力的综合值。

解释变量。企业经营发展的成果是各项资源投入的函数，按照企业运营可能需要的资源性质划分，包括土地资源、劳动资源、资金资源、技术资源、管理资源、创新资源、信息资源。在上市企业的年报资料中，一般不涉及土地资源、创新资源、信息资源等。所以，本文依据资料的可获得性，着重从劳动资源、资金资源和技术资源方面，选取用于解释企业盈利能力和发展能力的变量。在劳动资源方面，采用企业员工数(x11)、人均薪酬(x12)、员工薪酬总额占企业营业总收入比(x13)反映企业人力方面的投入(x1)。对资金资源，本文采用人均固定资产(x21)、人均流动资产(x22)、人均负债(x23)反映企业运营活动中的资金方面的投入(x2)。对技术投入方面，本文用研发活动(x3)表征企业的技术资源投入，采用的反映和表征指标主要是：人均研发支出额(x31)，研发投入力度(x32)。本文采用的分析变量见表1。

表1 分析变量说明

(二)数据资料描述：变量之间的相关性分析

对带有多个被解释变量的回归分析问题，如果被解释变量之间互不相关，完全可以转化为对每个被解释变量分别做一般的多元回归分析，反之则需要采用多重多元回归。本文选定了两个被解释变量，样本数据显示企业盈利能力(y1)和企业发展能力(y2)的相关系数为-0.124(见表2)，运用R.Fisher简单相关t检验法，检验结果显著不等于0。

根据样本资料，在本文所选择的解释变量中，部分解释变量存在显著性相关关系，比如：人均固定资产与人均流动资产(相关系数0.066，p<0.05)，人均研发支出与人均负债(相关系数0.079，p<0.01)，其他详见表2。在多重多元回归分析中，同样需要关注解释变量之间的共线性。这里，利用V.Farrar-G.Glauber方法检验共线性。由于

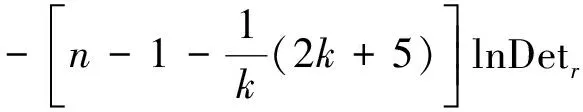
=637.298 2

(19)

式(19)中，n为样本观察规模，k为解释变量数目，Detr为表2中8个解释变量简单相关系数所构成的行列式的值。在自由度为0.5(k-1)k=28时，式(19)给出的卡方统计量χ2值发生的概率小于0.01，表明解释变量之间整体上不存在严重的共线性。

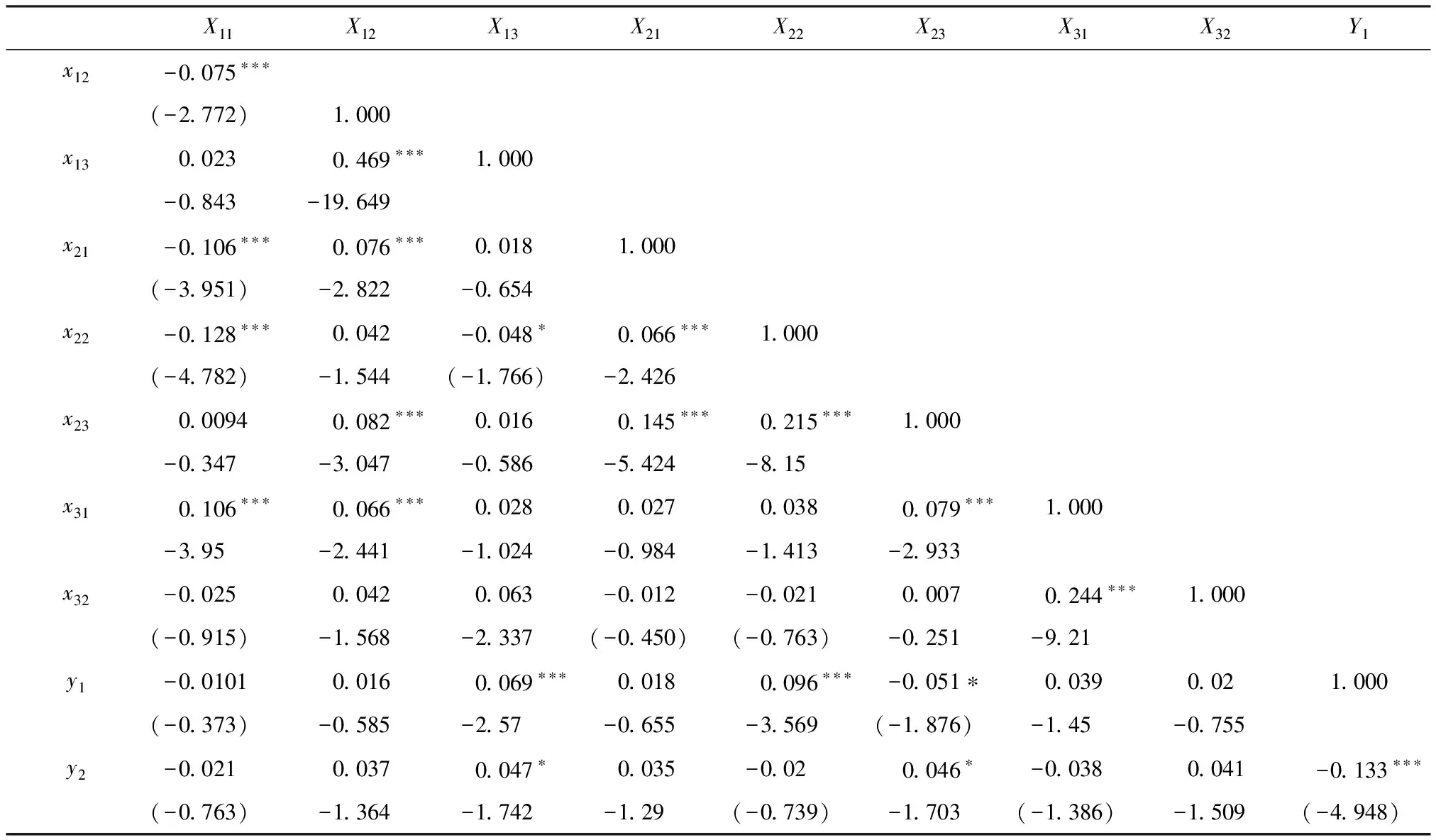
表2 变量之间的简单相关系数、检验统计量及检验结果

注：非括号中的数字为两两变量间的简单相关系数，括号中的数字为对应的t检验统计量值。*表示0.10水平显著，**表示0.05水平显著，***表示0.01水平显著。表中的数值四舍五入保留3位小数。

进行回归分析的重要条件之一，是解释变量与被解释变量之间存在某种程度的相关关系。由表2可知，解释变量与被解释变量不完全存在显著性相关关系。但对多重多元回归分析，至少要求所有被解释变量与全部解释变量之间整体上存在相关。为此，我们来进行典型相关分析。典型相关分析是简单相关分析的推广，主要说明的是一组变量线性组合(典型变量)与另一组变量线性组合(典型变量)之间相关关系[15]。本文的解释变量共有8个、被解释变量2个，分别把8个解释变量当成一组向量、2个被解释变量作为另一组向量，进行典型相关分析得到的第一对典型相关系数0.151、第二对典型相关系数0.101，根据检验结果，只需保留第一对典型变量即可，第一对典型相关变量的散点图见图1，表明8个解释变量与2个被解释变量之间大致存在着典型相关关系。

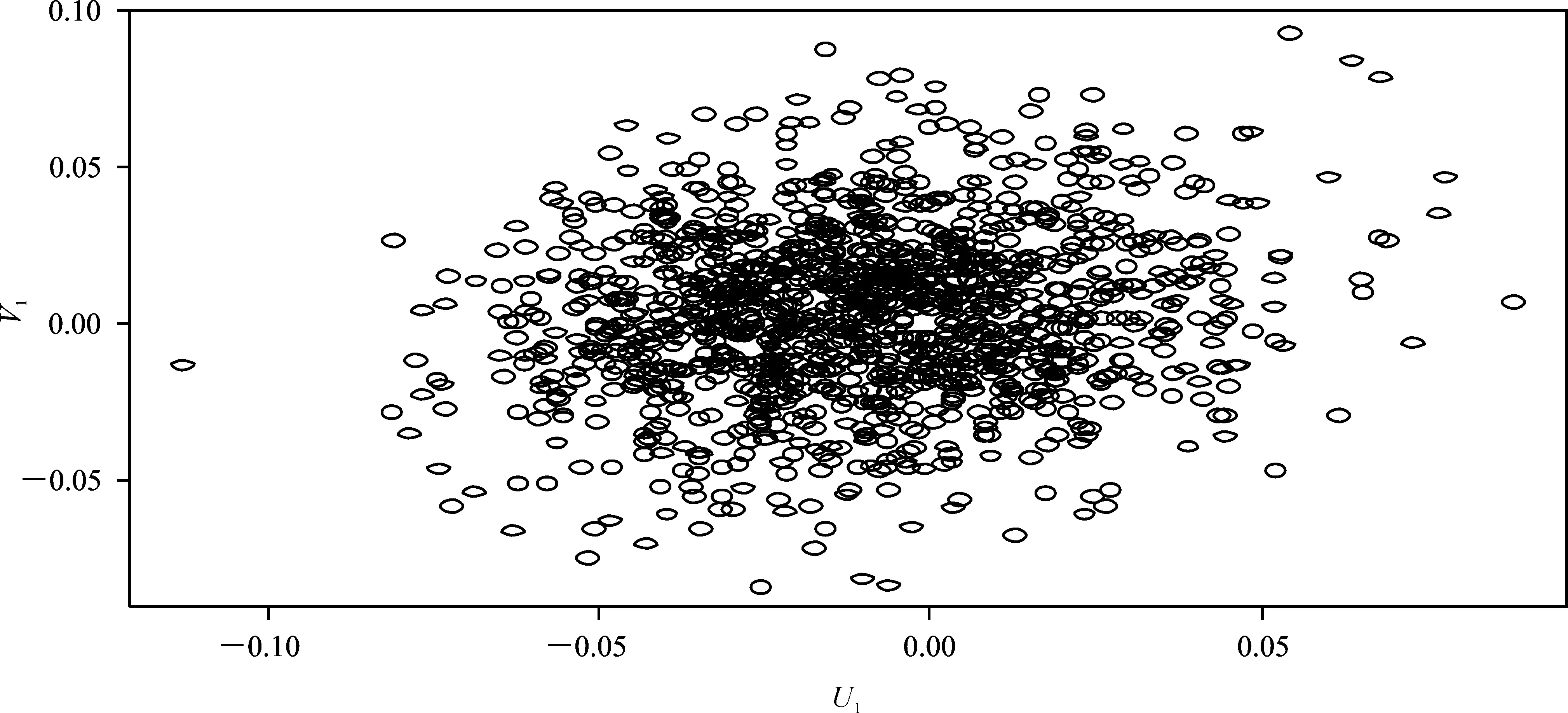
图1 第一对典型变量相关图

图1中，U1为所有解释变量的第一个典型变量，V1为全部被解释变量的第一个典型变量，(U1，V1)为第一对典型变量。

因此，在(y1，y2；x11，x12，x13，x21，x22，x23，x31，x32)之间建立多对多回归分析的相关性要求基本能得到满足。由式(2)，得到的求解结果为：

(20)

(三)回归效应检验

1.两组不同解释变量对同一被解释变量回归效应的比较

在这一问题的检验比较中，本文将人力投入的3个表征变量、资金投入的3个表征变量、研发投入的2个表征变量，对被解释变量企业盈利能力和发展能力的回归系数，通过式(13)分别两两做统计假设检验。其中，人力投入对企业盈利能力的综合回归效应为0.115(回归系数取绝对值后相加，这对比较回归效应大小不构成“危害”)，资金投入对企业盈利能力的综合回归效应0.139，由式(13)检验统计量F的值等于368.790，第一自由度1、第二自由度136 9-8=136 1时，该统计量取值发生的概率约为0.000，这是个发生概率非常小的“事件”，从统计意义上可以认为资金投入方面的人均固定资产、人均流动资产、人均负债对企业盈利能力的综合回归效应，比人力投入方面的企业员工数、人均薪酬、员工薪酬占企业营业收入比对企业盈利能力的综合影响要稍大。人力投入3个表征变量对企业发展能力的综合回归效应为0.142，资金投入3个表征变量对企业发展能力的综合回归效应为0.207，F检验统计量的值97.405，第一自由度1、第二自由度136 9-8=1 361时，该F统计量取值发生的概率也非常小，据此说明资金投入的人均固定资产、人均流动资产、人均负债对企业发展能力的综合回归效应，比人力投入方面的企业员工数、人均薪酬、员工薪酬占企业营业收入比对企业发展能力的综合影响也稍大。因此，对企业盈利能力和发展能力来说，企业资金投入因素要比人力投入因素表现要好些。资金投入的表征变量人均固定资产、人均流动资产、人均负债，与研发投入的表征变量人均研发、研发投入占营业收入比对企业盈利能力与发展能力综合回归效应的检验结果是：研发投入对企业盈利能力的综合影响效应0.023，按式(13)进行检验表明，比资金投入对企业盈利能力的综合影响效应小，研发投入对企业发展能力的综合回归效应0.198，也比资金投入对企业发展能力的综合影响效用稍小点。人力投入与研发投入对企业盈利能力、发展能力的综合影响效应的检验结论是：研发投入对企业盈利能力比起人力投入的综合影响效应小，但研发投入对企业发展能力的综合影响效应要大于人力投入。从制造业上市公司的样本来看，资金投入对企业盈利能力、企业发展能力的综合影响似乎比人力投入和研发投入都大些，研发投入对企业盈利能力的综合影响效应没有能显著展现出来，但它对企业发展能力的综合影响好于企业人力投入，与企业资金投入对企业发展能力的综合影响比较接近。

2.同一组解释变量对不同被解释变量回归效应的比较

该问题涉及到三个方面的检验比较，即：人力投入的表征变量对企业盈利能力、企业发展能力的综合回归效应差异，资金投入对企业盈利能力、企业发展能力的综合回归效应差异，研发投入对企业盈利能力、企业发展能力的回归效应差异。对这些假设采用的检验统计量由式(17)给出，数据检验结果表明：人力投入各表征变量对企业盈利能力的回归综合影响效应，与人力投入表征变量对企业发展能力的综合影响效应的F检验统计量值2.777，在第一自由度1、第二自由度1 366时，该检验统计量值的发生概率为0.099，如果显著性水平为0.05，人力投入对企业盈利能力和发展能力的综合影响不存在统计意义上的差别；资金投入表征变量对企业盈利能力的回归综合影响效应，与资金投入表征变量对企业发展能力的回归综合影响效应的F检验统计量值为5.567，在第一自由度1、第二自由度136 6时，该检验统计量值的发生概率为0.018，在显著性水平为0.05时，资金投入对企业盈利能力和发展能力的综合影响不一样，联系到回归系数的综合值，有可能说明了资金投入对企业发展能力的综合影响效应要大于对企业盈利能力的综合影响效应；研发投入表征变量对企业盈利能力的回归综合影响效应，与研发投入对企业发展能力的回归综合影响效应的F检验统计量值0.002，在第一自由度1、第二自由度1 367时，该检验统计量值的发生概率为0.969，这不是小概率事件，说明研发投入对企业盈利能力和发展能力的回归综合影响效应几乎相同。对某一组解释变量对不同被解释变量的回归影响效应，检验结果见表3。

表3 一组解释变量对不同被解释变量效应的比较表

注：表3和表4中的回归系数β事先都取绝对值。

3.两组不同解释变量对所有被解释变量回归效应的比较

两组不同解释变量对所有被解释变量回归效应的比较，主要是讨论：人力投入、资金投入表征变量对企业盈利能力和发展能力的回归综合影响是否存在显著性差异，资金投入、研发投入表征变量对企业盈利能力和发展能力的回归综合影响效应是否存在显著性差异，人力投入、研发投入表征变量对企业盈利能力和发展能力的回归综合影响效应是否存在显著性差异。对这些假设采用的检验统计量由式(18)给出，检验结果表明：人力投入、资金投入对企业盈利能力和发展能力的综合影响效应的F检验统计量为0.004，第一自由度1、第二自由度136 9-8=1 361时，该检验统计量取值发生的概率为0.952，说明人力投入、资金投入对企业所有发展目标的影响不存在差别；资金投入、研发投入对企业盈利能力和发展能力的回归综合影响效应的F检验统计量为0.643，第一自由度1、第二自由度1 369-8=1 361时，该检验统计量取值发生的概率为0.423，资金投入、研发投入对企业所有发展目标的影响不存在差别；人力投入、研发投入对企业盈利能力和发展能力的回归综合影响效应的F检验统计量为0.509，第一自由度1、第二自由度1 369-8=1 361时，该检验统计量取值发生的概率为0.476，说明人力投入、研发投入对企业所有发展目标的回归影响效应也不存在差别。两组不同解释变量对所有被解释变量回归效应比较的具体结论见表4。

表4 不同组解释变量对全部被解释变量效应的比较

四、小结

企业运营管理所产生的结果，是各种投入的资源有机结合的函数。投入的资源其性质不同，对企业运营结果的影响会存在一定的差异。分析和了解各类资源对企业运营结果的影响效应，有助于改善企业资源利用方案，提高企业资源利用效率，提升企业经营管理品质。

回归分析是应用十分广泛的一类统计学方法，在解释变量和被解释变量之间建立回归分析模型，然后利用回归系数的反映功能，可以帮助我们认识解释变量对被解释变量是否存在显著性作用，并且还能在解释变量对被解释变量回归效应之间做出大小或差别的比较。本文所做的研究工作主要体现在：将简单回归、多元回归分析中回归系数的比较，拓展到多重多元回归分析，包括：解释变量子集间对某个被解释变量的回归效应差异比较，同一解释变量子集对不同被解释变量的回归效应差异比较，以及不同解释变量子集对所有被解释变量的回归效应差异比较等。受样本数据资料“质量”的影响，实例应用的数据分析结果虽然不够理想，但至少能说明文中给出的有关这些问题的假设检验方法具有可行性。本文只对多重多元线性回归模型的回归效应比较做了论证说明，至于多重多元非线性回归问题，在线性化的基础上，相关的假设检验方法也可以使用。