Delay-performance optimization resource scheduling in many-to-one multi-server cellular edge computing systems
2019-10-15DuPengBaTeerZhangYuan
Du Peng Ba Teer Zhang Yuan
(1College of Automation & College of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China)(2National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)
Abstract:To further reduce the delay in cellular edge computing systems, a new type of resource scheduling algorithm is proposed. Without assuming the knowledge of the statistics of user task arrival traffic, the analytical formulae of the communication and computing queueing delays in many-to-one multi-server cellular edge computing systems are derived by using the arriving curve and leaving curve. Based on the analytical formulae, an optimization problem of delay minimization is directly formulated, and then a novel scheduling algorithm is designed. The delay performance of the proposed algorithm is evaluated via simulation experiments. Under the considered simulation parameters, the proposed algorithm can achieve 12% less total delay, as compared to the traditional algorithms. System parameters including the weight, the amount of computing resources provided by servers, and the average user task arrival rate have impact on the percentage of delay reduction. Therefore, compared with the queue length optimization based traditional scheduling algorithms, the proposed delay optimization-based scheduling algorithm can further reduce delay.
Key words:cellular system; delay; edge computing; resource scheduling
Cellular users tend to run computation-intensive applications which require many computing resources. To meet this requirement, the idea of cellular edge computing is introduced. First, one or more off-the-shelf computing units or servers are located in the base station (BS) to form a small-scale computing resource pool[1-2]. Then, users’ computing tasks are offloaded to the BS to run. The so-formed system is called the cellular edge computing system[3-4]. In such a system, there are two types of resources: the radio resource and computing resource. Therefore, the resource scheduling in the cellular edge computing system must take both types of resources into consideration. This paper studies the resource scheduling in the cellular edge computing system.
This paper focuses on the delay aspect of the resource scheduling. In cellular edge computing systems, there are four types of delays: transmission delay, communication queueing delay, execution delay and computing queueing delay. According to the way of incorporating delays into resource scheduling, existing works can be classified into three categories. For the first category, only transmission and execution delays are considered, but the communication and computing queueing delays are not considered[5-8]. For the second category, in addition to the transmission and execution delays, the queueing related delays are also considered. Furthermore, this type of algorithm assumed that the queue can be modelled as the traditional queue (e.g., the M/M/1 queue) so that the delay formulae of the queueing theory can be readily applied in the problem formulation[9-12]. For the third category of the algorithm, the queueing related delays are also considered. However, instead of using queueing theory’s delay formulae, Little’s law is used in this category. According to Little’s law, the average delay is proportional to the average queue length. Therefore, the delay minimization problem was transformed into the queue length minimization problem. Then, the scheduling algorithms were derived[13-16].
Generally, the third category of the algorithm is better than the second category, since it does not need any assumption on traffic’s statistics. However, the third category of the algorithm depends heavily on Little’s law. Actually, Little’s law can be inaccurate. Here is an example. Consider a queue where there are two newly arrived tasks at the beginning of each slot and each task needs half slot time to serve. LetQ(n) denote the number of backlogged tasks at the end of slotn. Then,Q(n) is always 2. On the one hand, according to Little’s Law, the average delay is 1 slot. On the other hand, it can be verified that the delay of the odd-numbered and even-numbered tasks is 0.5 and 1 slot, respectively, so the true average delay is 0.75 slot. Therefore, Little’s law is inaccurate for this example. The reason is that the queue length is not sampled frequently enough. Actually, for this example, if the queue length is sampled once every half-slot, the queue length will be 1 or 2 alternately, and then the average delay can be correctly calculated according to Little’s law.
Motivated by the above observations, this work tries to improve the third category of the algorithm by dropping the dependence on Little’s law. The key is to derive the formulae of the delays when there is no assumption on the traffic’s statistics so that the scheduling algorithm can be proposed by solving the delay minimization problem directly without using Little’s law.
1 System Model
Consider a cell consisting of one BS andIusers, in which time is slotted and the duration of each slot isTslot(unit:s). LetEidenote the number of cycles needed by the task of useri. For simplicity and without loss of generality, assume thatE1≤E2≤…≤EI. Assume that there areJcomputing servers in the BS. Each serverjcan provideFjcycles per second. Then, it will takeEi/Fjof serverjto execute one task of useri. For convenience, letαij=Ei/Fj/Tslotdenote the normalized execution time of one task of useriin serverj.
A task experiences two delays: the communication delay which is the sum of communication queue waiting time and transmission time, and the computing delay which is the sum of computing queue waiting time and execution time. The formulae of these two delays are derived as follows.
1.1 Communication delay
First, we derive expressions describing the evolution of communication queues. LetAi(n) denote the number of newly arrived computing tasks of useriduring slotn. LetNi(n) denote the number of tasks of useriselected by the resource scheduler during slotn. Furthermore, letUi(n) denote the number of backlogged tasks of useriat the end of slotn, which can be expressed as
Ui(n)=Ui(n-1)-Ni(n)+Ai(n)
(1)
whereUi(0)=0. There are three constraints onNi(n). First,Ni(n) must be the integer. Secondly,Ni(n) must not exceed the backlogged tasks in the queue, that is
0≤Ni(n)≤Ui(n-1)
(2)
Thirdly,Xi(n) must be limited by the communication capability of the air interface. For this constraint, some notations are needed. LetRidenote the number of subcarriers needed by userito offload a task request to the BS in one slot. The value ofRidepends on both the number of bits of each task request of useriand the channel condition of useri(e.g., path loss, fading, etc.). Specifically, the better the channel condition of useri, the smaller the value ofRi. Assume that there are a total ofRsubcarriers in the cellular edge computing system, and then this constraint can be expressed as
(3)

Wi(n)=Wi(n-1)+Ui(n-1)
(4)
Finally, we define
(5)
as the measure of the communication delay experienced by useri’s tasks.
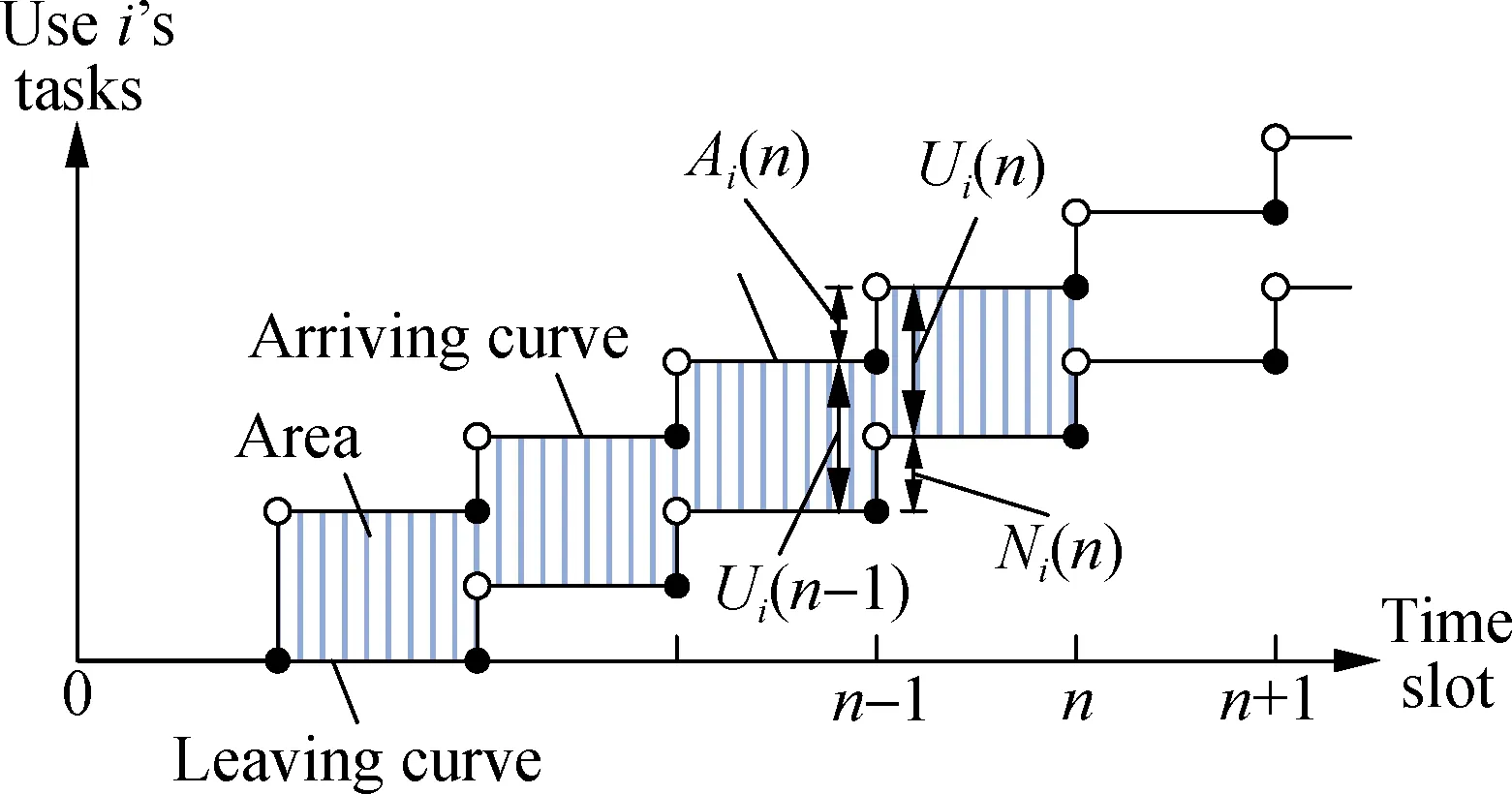
(a)
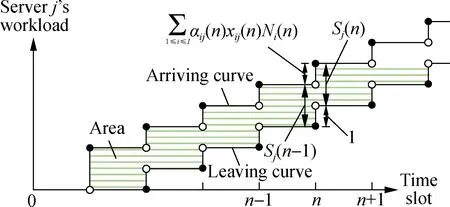
(b)
Fig.1The delay models. (a) The communication delay; (b) The computing delay
1.2 Computing delay
First, we derive expressions describing the evolution of computing queues. There areJcomputing queues. For eachj, letSj(n) denote the workload of backlogged tasks, that is, the number of slots needed to execute all these tasks by serverjat the end of slotn, which can be expressed as
(6)
(7)
Next, we derive the formula of computing delay. LetZi(n) denote the normalized total computing delay experiences by useriuntil slotn, which can be written as
(8)
whereZij(n) is the normalized total computing delay experienced by useri’s tasks in serverjuntil slotn. For this case, we use different methods to calculate the area between the arriving curve and leaving curve. LetDijh(n) denote the normalized delay (including execution time) experienced by theh-th task (1≤h≤Ni(n)). Then, we calculate the normalized area between the arriving curve and leaving curve as
(9)

Dijh(n)=
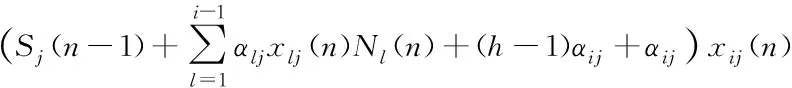
(10)
For convenience, let
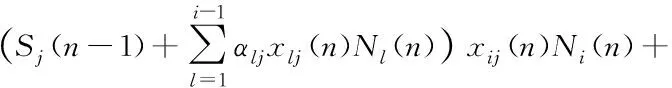
(11)
Then, we can have the formula ofZi(n) as
(12)
Finally, we define
(13)
as the measure of the computing delay experienced by useri’s tasks.
2 Resource Scheduling
2.1 Problem formulation
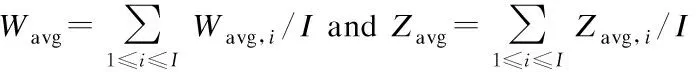
(14)
subject to the constraints in Eqs.(2), (3), (7) and thatNi(n) are integers andxij(n) are binaries. This optimization problem must be transformed into a solvable form. Actually, this optimization problem consists of two subproblems. The first subproblem is minWavgand the second subproblem is minZavg. The detailed forms of these two subproblems are derived as follows.
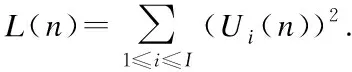
(15)
subject to the constraints in Eqs.(2), (3) and thatNi(n) are integers, whereUi(n-1) is the communication queue length measured for the previous slot.
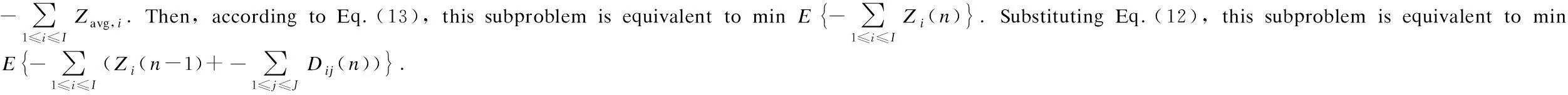
whereS(n-1)=[S1(n-1),…,SJ(n-1)].Using the concept of opportunistically maximizing an expectation, the above expression is minimized by the algorithm that observes the current queueS(n-1) and choosesxij(n) to minimize
Therefore, the subproblem minZavgcan be transformed into the following optimization subproblem for each slotn:
(16)
subject to the constraints in Eq.(7) and thatxij(n) are binaries, whereSj(n-1) in the expression ofDij(n) is the computing queue length measured for the previous slot.
According to the above derivations, the subproblem minWavgand minZavgcan be transformed into the optimization problem in Eq.(15) and Eq.(16), respectively. Therefore, the problem in Eq.(14) can be transformed into the following optimization problem for each slotn:
(17)
subject to the constraints in Eqs.(2), (3), (7) and thatNi(n) are integers andxij(n) are binaries.
2.2 Scheduling algorithm
Letgijdenote the partial derivative of the objective function in Eq.(17) with respect toxij(n), which can be calculated as
(18)
whereN=[N1(n),N2(n),…,NI(n)] andx=[x11(n),x12(n),…,xIJ(n)], respectively. Letfidenote the partial derivative of the objective function in Eq.(17) with respect toNi(n), which can be calculated as
(19)
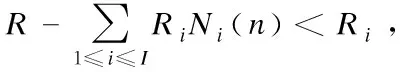
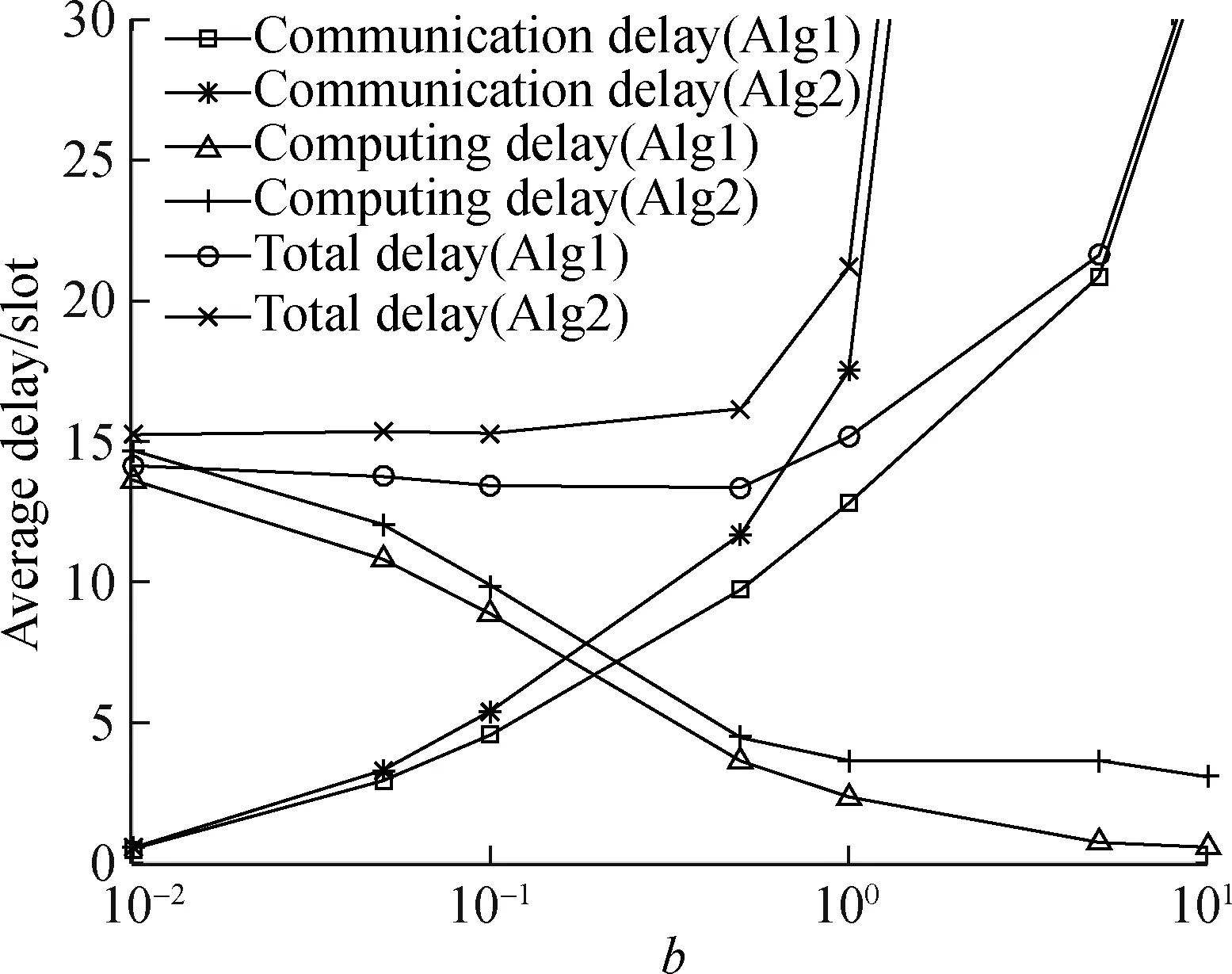
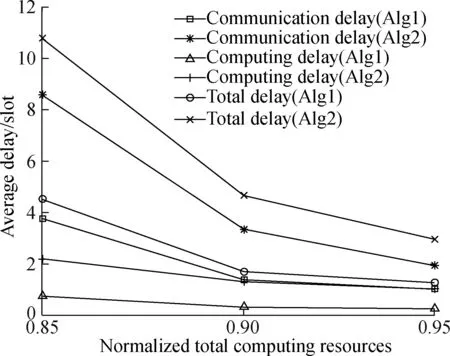
C(N,U,f)={i:fi<0,Ni(n) (20) wheref=[f1,f2,…,fI]. The proposed scheduling algorithm is as follows. First, initializeNi(n)=0 for eachiandU′i(n-1)=Ui(n-1) for eachi. The algorithm executes the following steps. Step1The values ofxare determined. Initially,xij=0 for each (i,j). For each useri, calculate the gradientgijfor eachjby substitutingNandxinto Eq.(18), then select the serverj*=arg mingijover allj, and assign userito this server (i.e., setxij*=1). Step2Update the values ofN. First, calculate the values off(N,U,x); secondly, select the useri*=arg minfiover all feasibleiC; thirdly, increaseNi*by one (i.e., letNi*←Ni*+1); fourthly, updateUi*(n-1)=Ui*(n-1)-1 andC(N,U,f). IfCis not empty, go back to Step 1; otherwise, the algorithm stops. Consider a time-slotted cellular communications system, in which the durationTslotof each slot is 10 ms. Assume that the total number of subcarriers provided by the cell isR=40. Assume that there areJ=2 servers. Unless otherwise stated, the values ofFjare set to be 2×105×[1, 1.5]. For the users in the cell, the parameters are set as follows. Assume that there areI=10 users. For each useri, assume that his/her tasks arrive according to a Poisson process with an average inter-arrival time ofTi. Unless otherwise stated, the value ofTiis set to be 5 slots; the values ofRiare set to be [2, 2, 2, 2, 3, 3, 3, 3, 4, 4]; and the value ofEiis set to be 1.5×103×(1+i/10) for useri. Fig.2 shows the simulation results ofWavg,Zavg, andWavg+Zavgwith differentbfor the proposed algorithm (i.e., Alg1) and the traditional algorithm (i.e., Alg2). For the curves in Fig.2, we have the following observations. First, both algorithms can trade-off between the communication delay and computing delay. With the increase inb, the computing delay decreases, while the communication delay increases. For example, whenbis increased from 10-2to 101, the computing delay of the proposed algorithm decreases from 13.638 6 to 0.570 8 slots, while the communication delay of the proposed algorithm increases from 0.502 8 to 32.674 5 slots, and the total delay increases from 14.141 4 to 33.245 3 slots. Secondly, the total delay of the proposed algorithm (i.e., the line with circle mark) is always better than that of the traditional algorithm (i.e., the line with cross mark). For example, whenb=10-1, the total delay of the traditional algorithm is 15.291 0 slot, while the total delay of the proposed algorithm is 13.426 6 slot, with a 12% off. This is due to the fact that the proposed algorithm directly minimizes the delay, while the traditional algorithm does not. Therefore, we can conclude that the delay performance of the proposed scheduling algorithm is better than that of the traditional algorithm. Fig.2 Impact of the parameter b and comparison with traditional scheduling algorithm Fig.3 Impact of the amount of computing resources provided by the computing server Fig.4 Impact of the average task arrival rate of users 1) The analytical formulae of the communication and computing queueing delays in the many-to-one multi-server cellular edge computing systems are derived without assuming the knowledge of the statistics of user task arrival traffic. 2) A novel resource scheduling algorithm which solves the delay optimization problem directly is proposed for the many-to-one multi-server cellular edge computing systems. 3) Under the considered simulation parameters, the proposed algorithm can achieve 12% less total delay, as compared to the traditional queue length optimization based algorithm. System parameters including the weight, the amount of computing resources provided by servers, and the average user task arrival rate have impact on the percentage of delay reduction.
3 Simulation Results
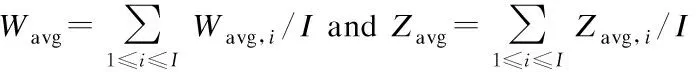
3.1 Comparison with traditional algorithm
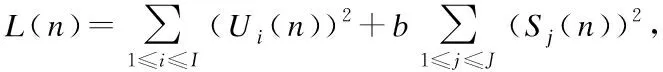
3.2 Impact of the amount of computing resources provided by the computing server
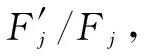
3.3 Impact of the average task arrival rate of users


4 Conclusions
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Tensile behaviors of ecological high ductility cementitious composites exposed to interactive freeze-thaw-carbonation and single carbonation
- Rolling contact fatigue nondestructive testing system for a bearing inner ring based on initial permeability
- Image denoising method with tree-structured group sparse modeling of wavelet coefficients
- Travel time prediction model of freewaybased on gradient boosting decision tree
- Projection pursuit model of vehicle emission on air pollution at intersections based on the improved bat algorithm
- Experimental investigation of oil particles filtration on carbon nanotubes composite filter
