基于修正Bertotti模型的变压器铁心谐波磁损耗计算与验证
2019-10-15赵志刚尹赛宁
赵志刚 ,魏 乐 ,郭 莹 ,刘 佳 ,杨 凯 ,尹赛宁
(1. 省部共建电工装备可靠性与智能化国家重点实验室,天津 300132;2. 河北省电磁场与电器可靠性重点实验室,天津 300132)
在输电系统中,变压器铁心一般由取向电工钢构成,因此,测量和分析取向电工钢的磁滞特性、损耗特性等磁性能是变压器产品设计及研发的基础[1].取向电工钢生产厂家所提供的材料磁性能数据通常采用标准爱波斯坦方圈测试系统或单片测量仪测量得到,该测量数据只能为制造商提供磁性材料的总损耗,不能获得磁滞损耗和涡流损耗在总损耗中所占比例[2-3].由于磁滞损耗和涡流损耗机理来源和解决方法不同,准确实现磁损耗的分离,显得十分必要.获取铁心中磁滞损耗和涡流损耗,采取相对应措施来降低磁损耗,对变压器优化设计具有重要的指导意义[4-5].
对于磁性材料的损耗计算模型基本上可以分为3类:第 1类是基于具有物理现象的磁滞模型,主要包括 Jiles-Atherton模型(简称 J-A模型)和 Preisach模型[6-7].其中 J-A模型是基于宏观能量的计算,而Preisach模型是基于磁畴运动在时间和空间上的统计.多年来,国内外研究学者致力于磁滞模型的研究,并通过磁性材料的磁滞特性解决铁磁材料的损耗计算问题,但实现过于复杂,需要大量的磁性能数据进行拟合和辨别参数,不适合工程应用.第 2类是经验公式法,Steinmetz在1982年总结了关于单位体积内磁损耗的经验公式[8],形式简单,涉及参数少,广泛应用于变压器、电机、电抗器等电磁设备的铁损计算,但无法实现磁损耗分离.第 3类是损耗分离法[9],建立在 3种不同效应对磁损耗的影响基础上,即磁滞损耗、涡流损耗以及异常损耗,在参数辨别不复杂的情况下,提高了计算精度,实现了磁损耗分离,同样得到了广泛的应用.
目前,这3类损耗计算模型在正弦激励条件下的损耗计算已相当成熟.由于特高压直流输电系统的发展,换流变压器作为其重要设备之一,负载运行时常会出现大量高次谐波,造成谐波污染,导致磁通发生畸变,严重威胁电网的安全稳定运行[10-11].对于非正弦激励条件下磁损耗的研究,学者Rudy Sevems将非正弦信号激励进行傅里叶分解,采用 Steinmetz公式分别计算谐波分量下的损耗,叠加得到总损耗值[12];Boglietti等[13]基于损耗分离模型,依据傅里叶分解理论发现谐波激励下的涡流损耗与电压有效值有关,磁滞损耗与电压平均值有关,尽管这两种方法简单易行,但硅钢片属于非线性材料,磁损耗与激磁频率和磁通密度峰值并不呈现简单线性关系,导致所得结果存在一定偏差,适用范围较为受限.此外,学者在经典 Steinmetz公式基础上进行修正,得到改进Steinmetz公式、广义 Steinmetz公式以及 Steinmetz波形系数公式,用于解决三角波、方波等激励下的磁损耗问题[14-19],但对于基波叠加高次谐波这种激励,应用结果的精确性有待验证.
针对谐波激励下磁损耗计算问题,本文基于简化的 Bertotti模型,通过最小二乘法,采用铁心工艺系数,确定正弦激励条件下铁损中磁滞损耗和涡流损耗.并在此基础上,引入谐波修正因子,对磁滞损耗和涡流损耗进行修正,实现了谐波激励下计算磁损耗目的,为变压器在设计与优化阶段磁损耗的准确计算提供参考.
1 磁性材料的损耗分离
一般发电机、电动机以及变压器运行在频率低于400Hz、磁通密度低于1.7T状态下,磁损耗主要包含磁滞损耗和涡流损耗两部分,可忽略异常损耗的影响.为考虑磁性材料的内应力、磁畴结构以及铁损成分等问题,本文基于忽略异常损耗的简化 Bertotti模型,实现磁损耗的分离,其公式为

式中:WT为铁损,W;Wh为磁滞损耗,W;We为涡流损耗,W;h、e分别为磁滞损耗和涡流损耗系数;f为频率,Hz;Bm为磁通密度峰值,T.
由于模型中的常数项以及磁通密度指数不是一成不变的,因此,需根据磁材料的损耗特性,重新对模型参数进行确定.本文采用标准爱波斯坦方圈测试系统,测量牌号为B30P105的取向电工钢,频率从25~400Hz,磁通密度峰值从 0.1~1.7T的磁性能数据,进行参数拟合的公式为

基于所测得到的取向电工钢磁性能数据,通过以下几个步骤实现模型中参数的确定和磁损耗的分离.
首先,为减少变量的影响,对式(2)做处理后得

式中:Win为磁滞损耗能量;Wsl为涡流损耗能量;x、y为磁通密度指数.通过提取磁通密度为 1T,频率为25~400Hz的磁性能数据,并计算铁损能量WT/f,如图 1所示,其中截距为特定磁通密度下的磁滞损耗能量.

图1 铁损能量分布Fig.1 Energy distribution of iron loss
然后,在不同磁通密度Bm作用下重复上述过程,得到关于不同磁通密度Bm下铁损能量分布,如图2所示.
进一步,提取不同磁通密度下的磁滞损耗能量,采用最小二乘法进行线性拟合,即可确定磁滞损耗的参数值,其拟合公式为

对于牌号为 B30P105的取向电工钢,h=0.004349,x=1.912885.
同理,确定涡流损耗能量的参数公式为

其中e=0.000057,y=1.827427.
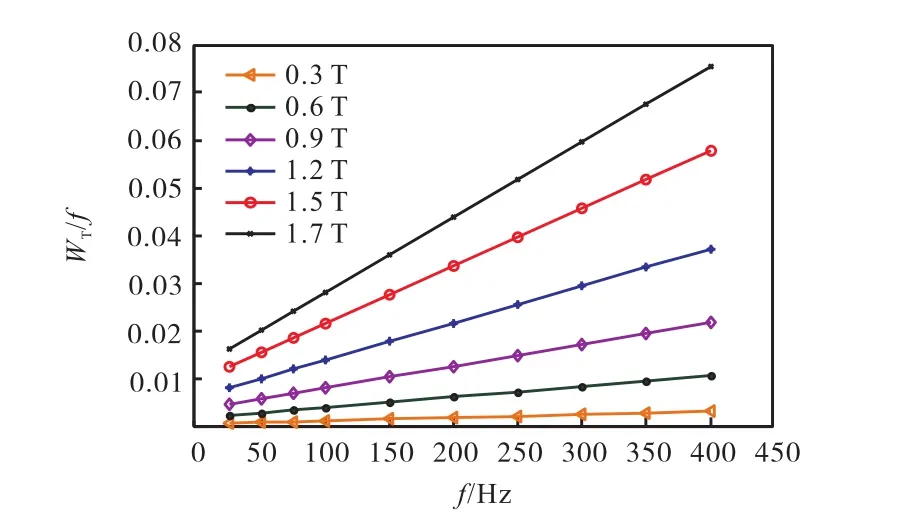
图2 不同磁通密度下铁损能量分布Fig.2Energy distribution of iron loss for different magnetic flux densities
因此,正弦激励下,牌号为B30P105取向电工钢的磁损耗计算模型为

相应的磁滞损耗和涡流损耗也可随之确定.
本文分别给出了频率为50Hz、150Hz和250Hz由爱波斯坦方圈测试系统所得测量值与采用损耗分离模型所得计算值对比分析结果,如图 3所示.可以发现,测量值与计算值具有较好的吻合性,验证了正弦激励条件下磁损耗分离模型的正确性.
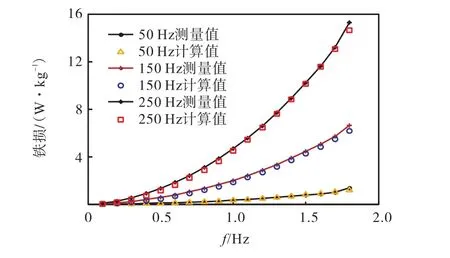
图3 铁损测量值与计算值对比Fig.3 Comparison of calculated and measured values
利用该损耗分离模型对工频(50Hz)下磁材料铁损中磁滞损耗和涡流损耗进行确定,如图 4所示.其中Pe=We/m,Ph=Wh/m,m为质量,kg.

图4 磁性材料的铁损分离Fig.4 Separation of iron loss for magnetic materials
图5给出了磁通密度在1.0T时不同频率下磁滞和涡流损耗占总磁损耗的百分比,可以看出,在低频段磁滞损耗占绝大部分,而随着频率的逐渐增加,磁滞损耗所占比例降低,而涡流损耗占据了主导地位,这是由于涡流效应随着频率的增加逐渐增加,从而导致涡流损耗增大.
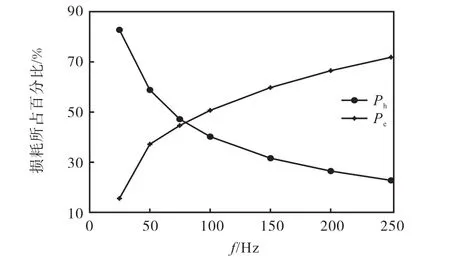
图5 不同频率下磁滞损耗和涡流损耗所占百分比Fig.5 Percentages of hysteresis and eddy current loss at different frequencies
2 铁心模型测试方法
基于完全按照电力变压器铁心的设计标准和叠装工艺设计并制作的变压器叠片铁心模型,搭建谐波激励条件下的实验测试平台,对磁损耗特性进行实验研究,如图 6所示.其中变压器叠片铁心模型采用45°全斜接缝,每级两片、三级步进 5mm搭接的切装工艺制作而成,图 7为变压器叠片铁心模型结构[20].需要指出的是该模型的叠积方式和结构与实际变压器产品相近,因此可以反映实际变压器产品的主要电磁性能.

图6 磁性能测试平台Fig.6 Magnetic energy testing platform
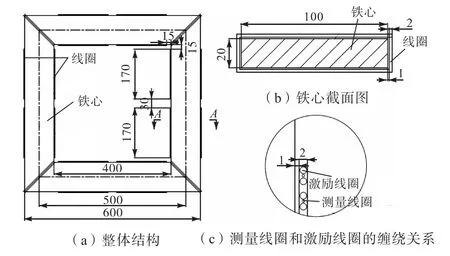
图7 变压器叠片铁心模型结构Fig.7 Structure of transformer laminated core model
对于谐波激励条件下的铁心磁性能测试,本文实验过程中通过调整励磁电压,控制变压器铁心内的磁通密度波形为

式中:B1为基波幅值;Bn为n次谐波幅值;φn为n次谐波相位.
谐波含量以及谐波相位差分别表示为

式中:θn为谐波相位差;kn为谐波含量;φ1为基波相位,本文设置基波相位为 0°.由于变压器铁心原副边匝数相同,可近似认为激励电压与感应电压相等,根据电磁感应定律,激励电压与磁通密度的关系为

式中:E(t)为激励电压,V;N为线圈匝数;S为铁心横截面积,mm2;B为磁通密度瞬时值,T.按式(12)控制激励电压的波形,实现对变压器铁心中磁通密度波形的控制.
3 磁损耗计算模型
3.1 铁心模型损耗分离的确定
由于爱波斯坦方圈与实际变压器铁心的结构不同,导致硅钢片的材料性能与实际产品的铁心性能存在差异,铁芯工艺系数 BF可准确把握二者之间的差异,其计算公式为

式中:mweight表示变压器铁心质量,kg;Ps为标准爱波斯坦方圈所得比总损耗,W/kg.
本文采用变压器叠片铁心模型,测量工频条件下的损耗特性,根据式(13),得变压器铁心的工艺系数,如图8所示.可以看出,工艺系数不是常数,随磁通密度变化而变化,在1.10~1.15之间波动.
假定工艺差异对铁心中的涡流损耗和磁滞损耗影响相同,将磁性材料在工频下的铁损分离数据与变压器的工艺系数相结合,得到变压器磁损耗的分离数据,如图9所示.
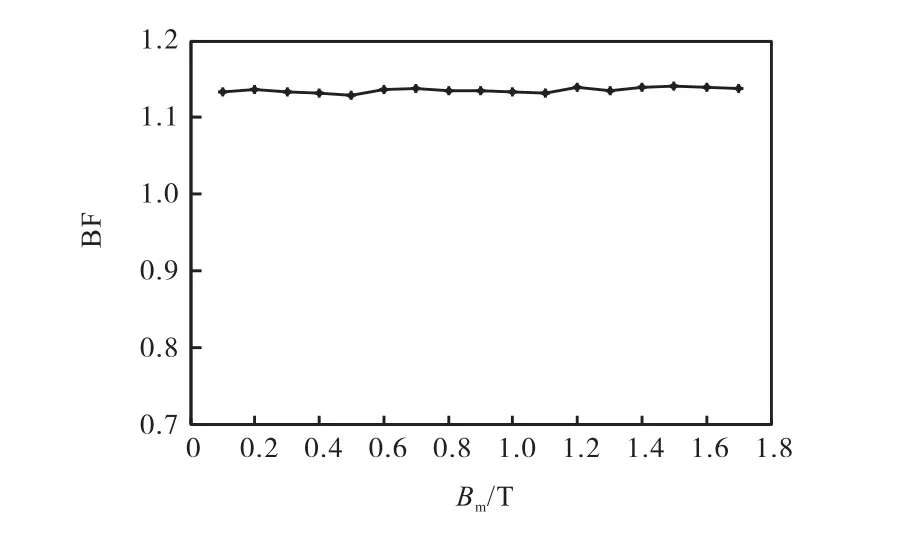
图8 工艺系数的变化曲线Fig.8 Change curve of process coefficient
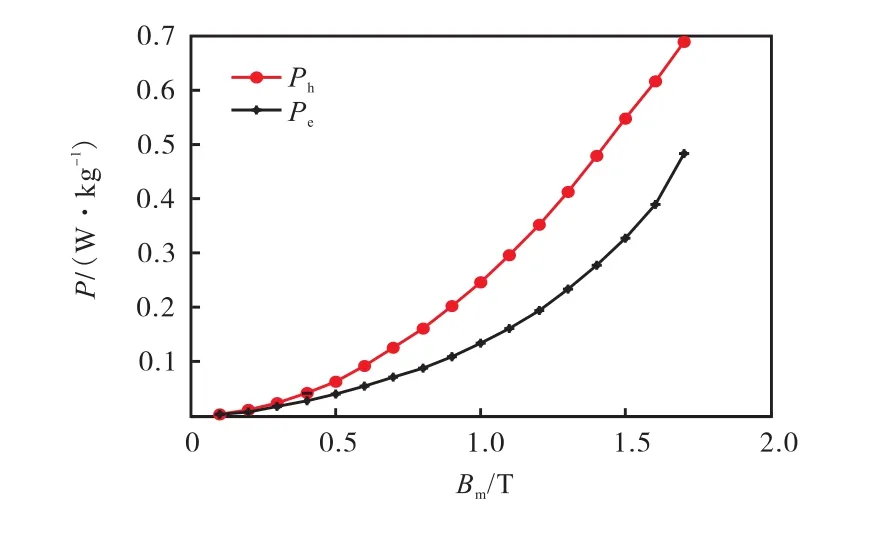
图9 磁损耗分离Fig.9 Separation of magnetic loss
3.2 磁损耗的修正
当磁通密度中含有谐波分量时,变压器铁心中的涡流会发生变化,与Bm相同的正弦激励下的磁滞回线相比,谐波激励下的磁滞回线矫顽力增加,并且磁通密度波形中的每一个波动,在磁滞回线中都有相应的局部回环与之对应,如图 10所示.局部磁滞回环是导致磁损耗增加的原因.

图10 含谐波分量的磁通密度及磁滞回环Fig.10 Magnetic flux density and hysteresis loop with harmonic components
在复杂激励条件下,由于局部磁滞回环的出现,导致 Bertotti模型不再适用.由式(9)可知,磁通密度的波动随高次谐波的幅值、相位以及阶次变化而变化,因此,对磁损耗的进行修正时,需同时考虑导致磁通密度发生畸变的三要素.著名学者 Lavers等[21]对磁滞损耗和涡流损耗做了进一步修正,通过大量的实验研究,得到磁滞损耗修正因子,即

式中:ΔBi为磁通密度局部波动的峰峰值;M为函数极值的个数,如图 11所示;Bp为谐波激励下磁密整体峰值;k为一个与磁性材料属性相关的系数,取值范围为 0.6~0.7之间.需要指出的是,ΔBi仅考虑正半轴中磁通密度波动.

图11 磁通密度畸变波形Fig.11 Magnetic flux density distortion waveform
对于标准正弦激励下涡流损耗表示[22]为

类似地,按式(9)所控制的谐波磁通密度波形,涡流损耗可表示为
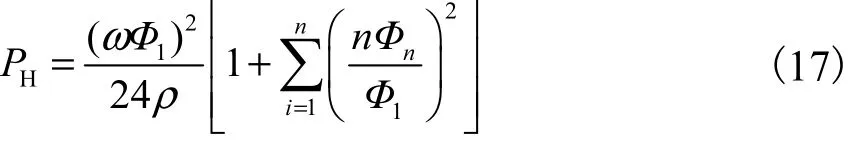
因此,涡流损耗修正因子可表示为

将式(18)做进一步简化得

按式(9)中磁通密度的控制方法,图12给出了不同谐波相位差下,基波叠加5次谐波下磁滞损耗修正因子和涡流损耗修正因子随谐波含量的变化曲线.
可以看出,尽管涡流损耗修正因子和磁滞损耗修正因子都随着谐波含量的增加而增大,但谐波含量对涡流损耗修正因子的影响更大.此外,谐波相位差的增加,两个修正因子也逐渐增加,相位差在 180°时修正因子最大.由此推论出在谐波含量和谐波阶次一定时,谐波相位差在180°时磁损耗值最大.
综上所述,谐波激励下磁损耗模型可表示为
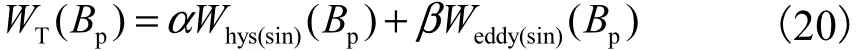
式中:WT(BP)为谐波激励下的磁损耗;α为磁滞损耗修正因子;Whys(sin)(BP)为工频且峰值 BP下的磁滞损耗;β为涡流损耗修正因子;Weddy(sin)(BP)为工频且峰值BP下的涡流损耗.

图12 修正因子变化曲线Fig.12 Correction factor curves
3.3 磁损耗验证
基于Bertotti模型,学者Rudy Sevems将非正弦信号傅里叶分解后分别计算,通过叠加得到磁损耗值,本文将其称之为模型 A,即将非正弦磁通密度波形进行傅里叶变化,采用 Bertotti模型分别计算各次谐波损耗值,叠加得到总磁损耗;此外,基于 Bertotti模型采用修正因子处理技术计算谐波磁损耗的方法称之为模型B.
表 1和表 2分别给出了相位差为 0°和 180°、基波叠加 30%的 3次谐波下采用 A、B两种模型计算出的谐波磁损耗.可以发现,模型 A 相位差为 0°和180°磁损耗值不变,即无法考虑谐波相位对损耗的影响,此外,磁性材料在磁通密度较低,近似呈线性阶段,采用模型A可以得到较好的计算结果,而随着磁性材料非线性属性的出现,会出现较大偏差,模型 B则可以很好地弥补模型 A的不足,计算值与测量值有较好的吻合性,证明了模型B的正确性.

表1 相位差为0°时磁损耗计算结果Tab.1 Calculation of magnetic loss when phase difference is 0°

表2 相位差为180°时磁损耗计算结果Tab.2 Calculation of magnetic loss when phase difference is 180°
为进一步对损耗计算模型进行验证,表3给出了相位差分别为0°和180°,基波叠加 30% 5次谐波的测量值与计算值.表4给出了基波+20% 3次谐波+20% 5次谐波的测量值与计算值.表5给出了基波+10% 3次谐波+10% 5次谐波+10% 7次谐波的测量值与计算值.表6给出了基波+5% 3次谐波+5%5次谐波+5% 7次谐波+5% 9次谐波的测量值与计算值.
通过表3~表6中数据对比可知,引入的磁滞损耗和涡流损耗修正因子,综合考虑了谐波含量、谐波相位以及谐波阶次对磁损耗的影响.可以看出,计算误差在 5%以内,因此采用 B模型计算谐波磁损耗,对于产品电磁设计阶段具有重要的参考价值,可提供有效的分析方法和必要的数据支撑.

表3 磁损耗计算结果对比Tab.3 Contrast in magnetic losses

表4 磁损耗计算结果验证ⅠTab.4 Verification of calculated magnetic loss resultsⅠ
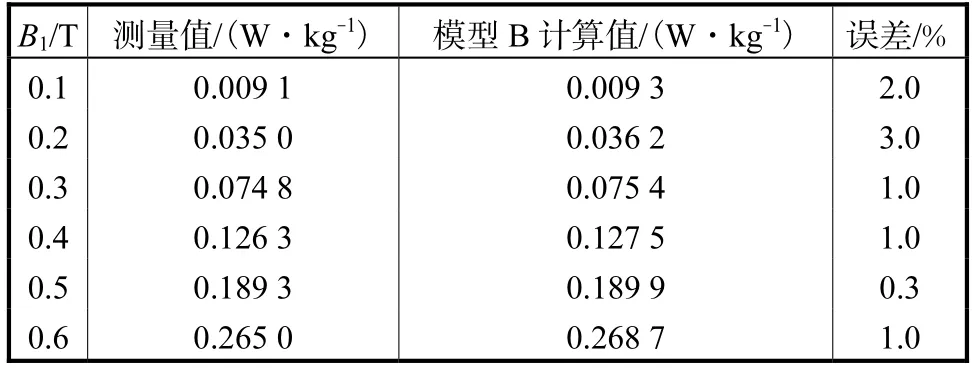
表5 磁损耗计算结果验证ⅡTab.5 Verification of calculated magnetic loss resultsⅡ

表6 磁损耗计算结果验证ⅢTab.6 Verification of calculated magnetic loss resultsⅢ
4 结 论
(1) 采用简化的 Bertotti模型,通过数据拟合方式,实现了正弦激励下磁性材料的铁损分离,并采用工艺系数校正,得到了变压器铁心磁损耗分离数据,并通过对不同频率下磁滞和涡流损耗的确定,发现在低频段磁滞损耗占绝大部分,而随着频率的逐渐增加,磁滞损耗所占比例降低,而涡流损耗占据了主导地位.
(2) 本文引入修正因子,对磁滞损耗和涡流损耗进行修正,实现了谐波激励下的变压器铁心损耗计算,损耗误差基本保持在 5%以内,满足工程所需的精度要求,适合工程应用.
(3) 以修正后的铁心损耗计算值作为损耗评估的基准值,对优化设计以及提高变压器产品性能具有重要的指导意义.
