基于EM-EKF算法的RLV再入段气动参数辨识

窦立谦，杜苗苗，张秀云，王跃萍

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 飞行控制航空科技重点实验室(航空工业自控所)，西安 710065)

可重复使用运载器不仅飞行速度快、高度范围广，而且其发射成本与传统的天地往返系统相比较低[1-2]，是一种兼具航空器和航天器特点且能在未来天地往返的重要工具[3].但是，在其从太空返回地球的过程中，RLV将面临再入段带来的严峻考验.在再入返回段中，由于RLV飞行速度快，飞行状态变化剧烈，气动参数表现为不确定和快时变的特点[4]，导致RLV气动的耦合性和非线性增强，使气动模型难以设计和控制，降低了飞行器的稳定性[5].因此，根据RLV再入返回段的量测数据，进行气动参数辨识研究，对 RLV的气动模型的建立和控制设计具有很重要的意义.

在已知模型结构的前提下对气动参数进行辨识，是根据试验数据估计模型中未知参数的过程.在实际飞行中，系统噪声是往往不可忽略的，这便要求参数辨识算法的精确性.用于研究气动参数辨识的算法有最小二乘法、极大似然算法、卡尔曼滤波算法、扩展卡尔曼滤波算法，其中卡尔曼滤波、扩展卡尔曼滤波在参数辨识中应用较为广泛，但是，卡尔曼滤波适用于线性系统的状态估计问题，而 EKF适用于非线性系统的状态及参数估计的问题，且已广泛应用于飞行器气动参数辨识问题的研究[6].

众所周知，用于描述 EKF测量和过程噪声的先验统计数据是需要假设为已知数据[7].这些噪声特性的设置影响 EKF算法在参数估计时的成功或失败.特别是在噪声统计特性随时间变化的环境中，EKF算法会导致较大的估计误差甚至会出现偏差.因此，初始状态、测量噪声协方差矩阵和过程噪声协方差矩阵的选择，在控制 EKF学习算法的收敛中是非常重要的.故需要将噪声的统计特性也视为未知参数，这便属于存在隐含变量的参数辨识问题.最大期望算法是一种用于含有隐变量参数模型的迭代的极大似然估计算法，Bavdekar等[8]曾经将EM 算法用于非线性系统的参数估计，文献[9]使用EM 算法对噪声协方差进行了精确的估计.因此本文采用 EKF算法对 RLV气动模型的未知气动参数进行估计，使用 EM 算法对噪声的统计特性进行估计，并与 Rauch-Tung-Striebel(RTS)平滑器相结合，完成其最大化的求解过程，能够在精确的噪声特性的基础上，更好地提高EKF算法参数估计的精度.

1 可重复使用运载器(动力学)模型

考虑类X-37B构型的RLV飞行器再入段六自由度方程[10-12]为

式中：x、y、z、v、α、β、φ、θ、ψ、p、q、r分别为 RLV的纵向位移、侧向位移、飞行高度、飞行速度、攻角、侧滑角、滚转角、俯仰角、偏航角、滚转角速度、俯仰角速度、偏航角速度；惯性积分别为沿x、y、z轴的转动惯量；L、D、Y分别为升力、阻力和侧力；、、分别为 RLV的滚转力矩、俯仰力矩和偏航力矩；其表达式为

式中aδ、eδ、δro分别为飞行器的副翼偏转角、升降舵偏转角和方向舵偏转角.

由于飞行器力矩Cl、Cm、Cn的参数与气动力CL、CD、CY的参数辨识类似，因此，本文只对气动力部分参数进行辨识，力矩参数的相关辨识过程不再赘述.

2 算法理论

2.1 非线性状态空间模型

考虑非线性系统的状态空间模型如下.

状态方程和观测方程分别为

式中：Xk、Yk分别为系统的状态向量和观测向量；η为待估计的未知参数；u为系统的输入向量；f(·)为非线性函数；Γw为σ×p维的系统过程噪声输入矩阵；H为τ×n维的观测矩阵；为e维的系统随机过程噪声序列；为τ维的系统随机观测噪声序列.过程噪声和观测噪声假设为满足高斯零均值分布，且两者相互独立，即

式中：Q为过程噪声wk的e× e维对称正定方差矩阵；R为观测噪声kχ的τ×τ维对称正定方差矩阵.

气动力参数主要与飞行器模型中式(1)的v、z、α、β相关，因此辨识时只考虑这 4个状态方程即可.假设系统噪声只对状态量v、z、α、β产生干扰影响，角度及角速度等均可测.式(1)中关于v、z、α、β对状态方程变换如下.

状态方程为

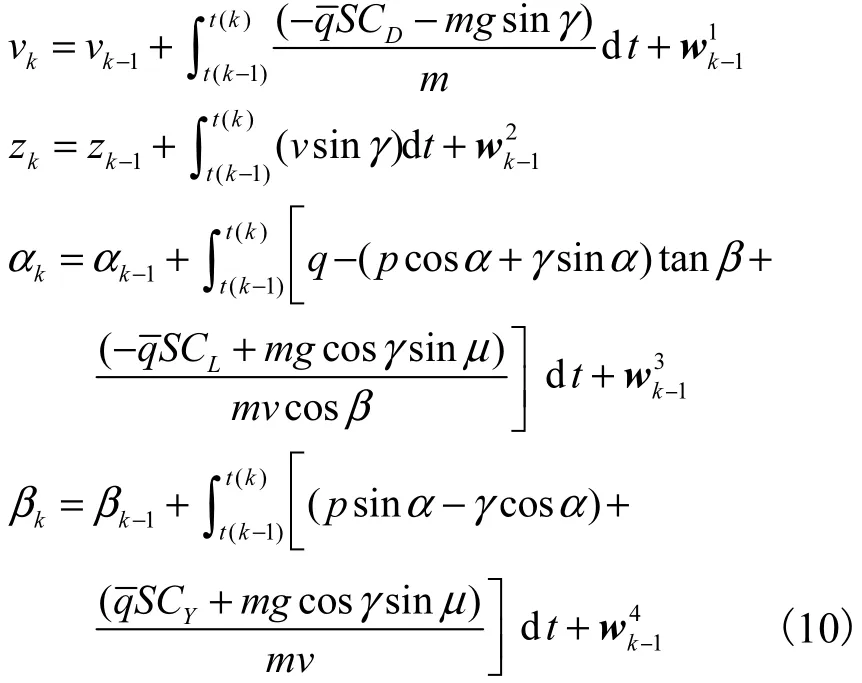
观测方程可表示为

至此，类 X-37B RLV 模型已转换为式(7)和式(8)所示的非线性系统的状态空间模型，下文将针对此状态空间模型，对气动参数进行辨识研究.

2.2 扩展卡尔曼滤波算法

扩展卡尔曼滤波(EKF)是一种间接对参数进行辨识估计的算法，其原理是将系统的参数估计问题转化为对系统状态进行估计，即要对原始的状态向量进行扩维，得到由未知参数和原始状态向量组成的扩维状态向量，即，从而得到新的状态空间模型为

假设扩维状态向量的初值X0服从均值为μ、方差为P0的高斯分布，基于由式(13)和式(14)组成的扩维状态空间模型，使用扩展卡尔曼滤波对扩维状态向量进行预测和更新的过程如下.

1) EKF预测

状态预测方程为

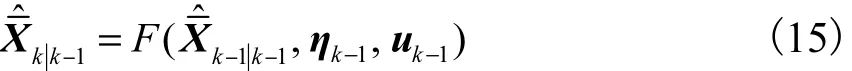
观测预测方程为

协方差矩阵预测方程为

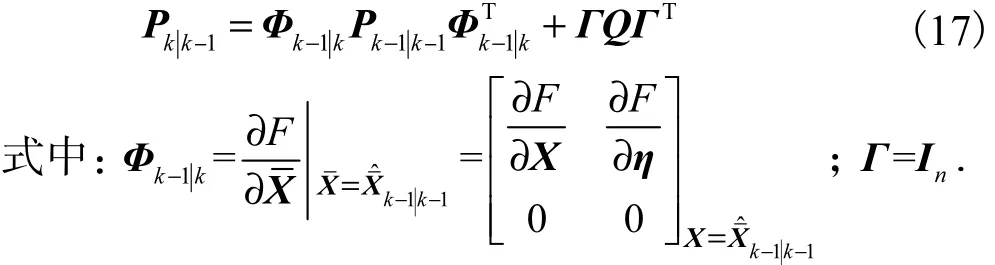
2) EKF更新

Kalman滤波增益更新公式为

状态更新公式为

协方差更新公式为

由上述的 EKF过程，可以知道状态估计的精度与扩维状态初值的分布特点(μ，P0)、噪声的特性(Q，R)有着密切联系，假设模型的统计量λ(μ，也是未知的，即在估计系统参数η的同时，需要通过 EM 算法对λ进行估计[13]，从而得到参数η更准确的估计值.

2.3 EM-EKF算法

完成EM算法对上述参数λ的估计，首先需要获得完整数据的概率函数.假设系统的初始条件、状态向量和观测向量的变化均满足高斯分布.由马尔可夫链可得其表达式为

则对数似然函数的表达式为

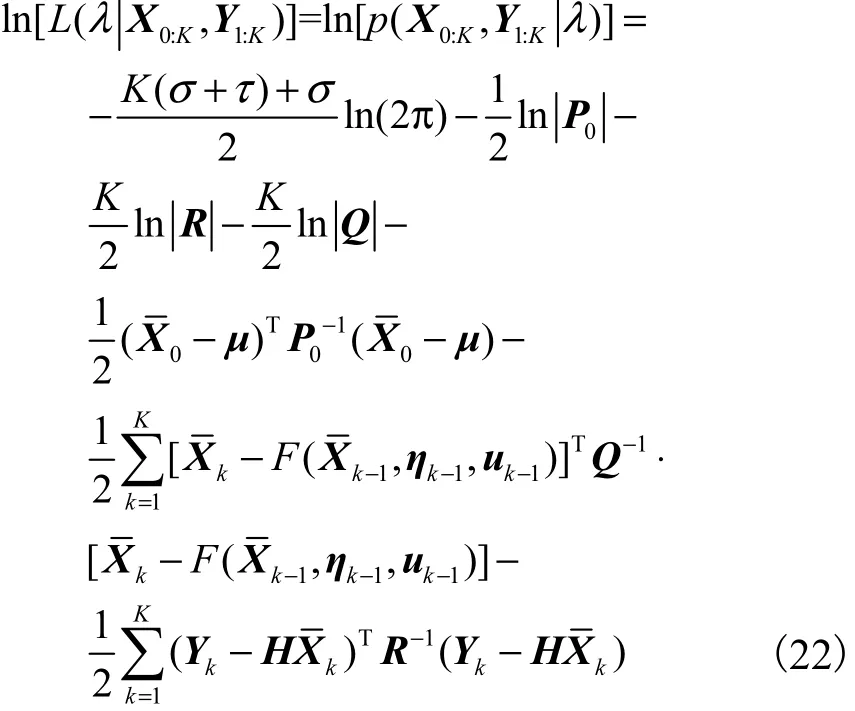
3) 求期望

EM 是一种不断迭代的优化算法，假设当前的迭代次数为i，令辅助函数为

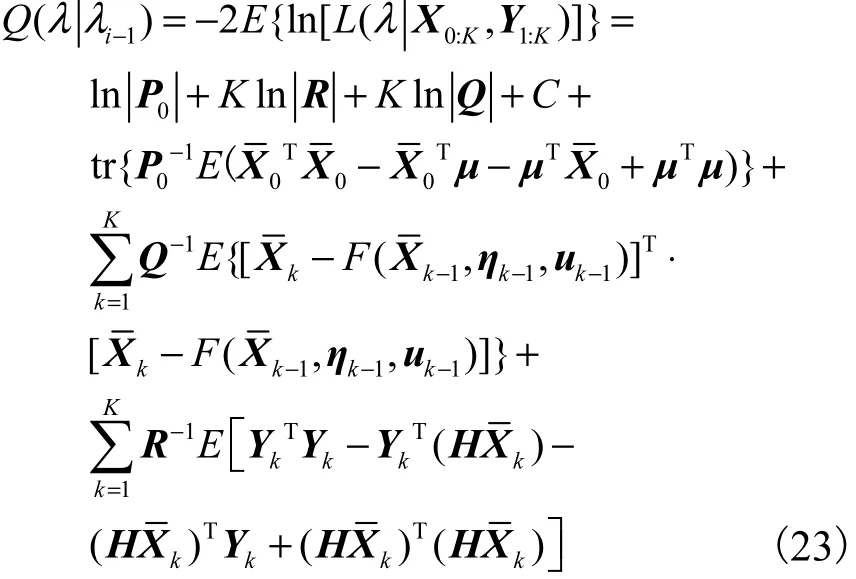
其中，常数C=[K(σ+τ)+σ]ln(2π).

令

在第2.2节中所介绍的EKF算法流程为状态的前向传播过程，为了计算的值，需要应用 Rauch-Tung-Strieber(RTS)平滑器的后向传播过程，其原理如下.

式中：Jk为平滑器增益；均值初值为；互协方差初值为；方差初值为

故

又由于

则

同理可得

故辅助函数

为了得到参数λ的最佳估计值，需要对辅助函数极大化，即通过式(37)对参数μ、P0、Q、R求偏导数，并令其偏导数等于0，可得表达式为

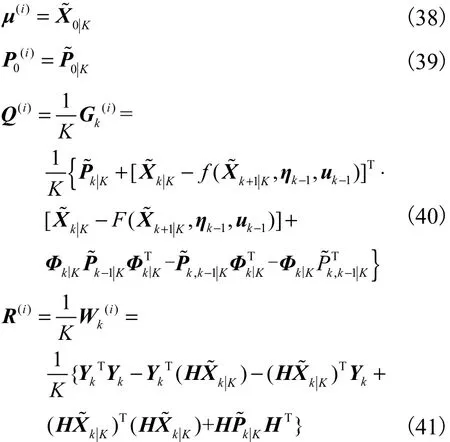
下文将在由式(38)～式(41)得到 EKF初始状态、测量和过程噪声协方差矩阵最佳估计值的基础上，采用EKF算法对未知气动参数η进行精确估计.

3 参数辨识结果与分析

考虑 RLV再入段飞行跨度大，范围为 20～80km，气动起主要作用的区域范围为 30～60km，且飞行器再入阶段的攻角变化范围较大.故以其飞行高度和攻角为基准，每10km一个区间划分飞行器的飞行阶段，分别进行气动参数的在线辨识，区间划分如下.

区间 1：高度变化范围为 50～60km，攻角范围为 40°～45°，速度范围为 4947～6281m/s.

区间 2：高度变化范围为 40～50km，攻角范围为 35°～40°，速度范围为 3176～4947m/s.

区间 3：高度变化范围为 30～40km，攻角范围为 30°～35°，速度范围为 1509～3176m/s.

由于在不同区间的状态量、观测量和待辨识的气动参数均一样，只是在不同区间的初值和参数值发生改变，故只需介绍一个区间内的气动参数辨识过程，下文将以区间1的气动参数辨识过程为例.

基于方程(11)与(12)可得：RLV 气动参数辨识的状态向量，观测向量Yk=，待辨识的气动参数，扩维状态向量，输入向量

为了减少初值的设置对辨识结果的影响，选取待辨识参数初始值为 0，扩维状态向量的协方差P、过程噪声和测量噪声的方差矩阵Q、R的初值均为单位阵

状态向量的初始值选取如下：

则扩维状态向量初始值为

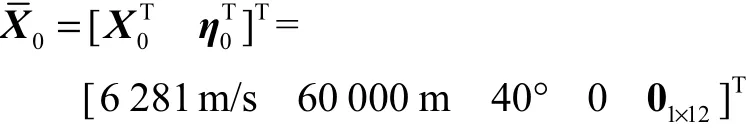
系统常值参数如表1所示.

表1 系统常值参数Tab.1 System constant parameters

分别采用 EM-EKF算法(迭代次数为 2000)与极大似然(ML)算法对区间 1中的气动参数进行辨识，其结果如表2所示.

表2 区间1参数辨识结果Tab.2 Parameter identification results of interval 1

同理可得，其他两个区间的气动参数辨识值如表3和表4所示.

表3 区间2参数辨识结果Tab.3 Parameter identification result of interval 2

以机理模型的原始数据、EM-EKF(滤除噪声)和极大似然(未滤除噪声)算法(ML)的气动参数辨识值为基础，基于区间 1分别分析攻角、侧滑角、副翼偏转角、升降舵偏转角和方向舵偏转角对升力、阻力、侧力、俯仰力矩、滚转力矩和偏航力矩系数的影响，具体对比效果如图1～图6所示.

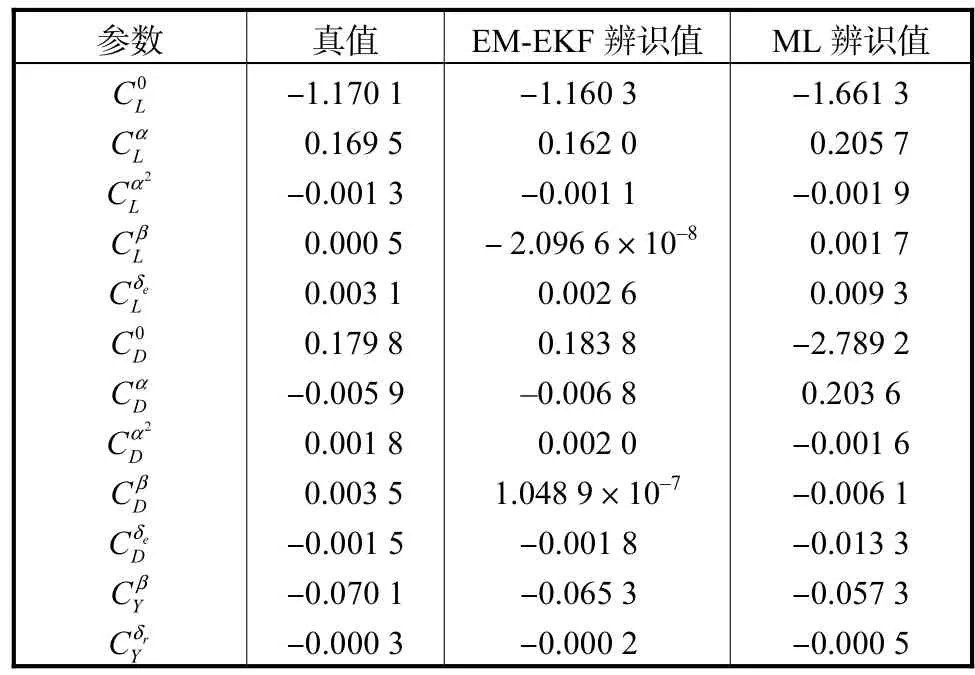
表4 区间3参数辨识结果Tab.4 Parameter identification result of interval 3

从图1～图6的曲线可以看出，虽然三者之间的误差不是很大，但是以 EM-EKF算法的气动参数辨识值为基础的系数曲线能够较好地与原始数据的曲线相拟合，即在系统噪声存在的情况下，采用 EMEKF算法对气动参数具有较好的辨识效果.

图2 阻力系数值的比较Fig.2 Comparison of the drag coefficient values

图3 侧力系数值的比较Fig.3 Comparison of the lateral force coefficient values

图4 偏航力矩系数值的比较Fig.4 Comparison of the yawing-moment coefficient values

图5 滚转力矩系数值的比较Fig.5 Comparison of the rolling-moment coefficient values

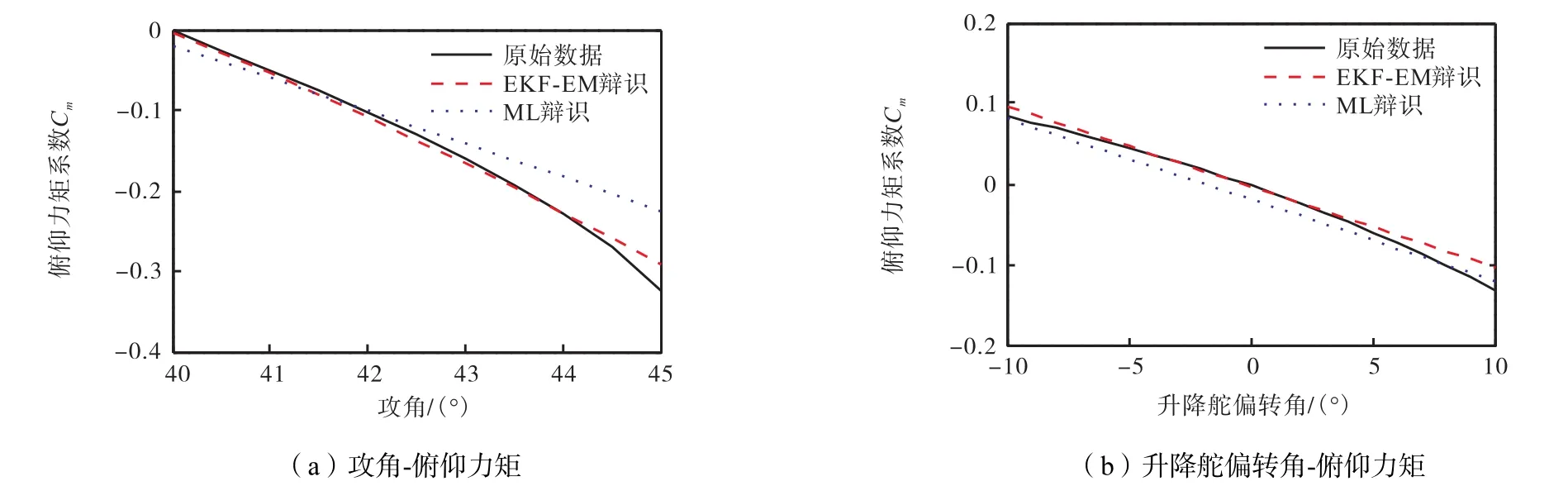
图6 俯仰力矩系数值的比较Fig.6 Comparison of the pitching moment coefficient values

4 结 语

本文针对RLV飞行器再入段气动特性的强耦合性和非线性等问题，在系统噪声存在的前提下，提出了一种基于 EM-EKF算法的气动参数辨识方法.首先，以飞行高度和速度为基准，将RLV再入段分为3个飞行区间；然后，分别对 3个区间的气动参数进行参数辨识；在辨识的过程中，考虑系统噪声的存在，采用EKF算法对状态和气动参数进行估计以滤除噪声，之后为了减少测量和过程噪声的先验统计量的设置对EKF辨识结果带来的影响，在EKF辨识算法的基础上，结合 EM 算法更精确的估计 EKF先验统计量，能够更好地提高 EKF算法对气动参数估计的精度；最后，通过将提出的EM-EKF结合的参数辨识算法与极大似然方法的辨识值对各种气动系数影响进行仿真对比，验证了辨识方法的准确性.