基于二阶锥规划的有源配电网多时段负荷恢复方法

于 浩，刘家恺，宋关羽，张孟珍，冀浩然，王成山

(智能电网教育部重点实验室(天津大学)，天津 300072)

配电系统是未来能源系统的重要组成部分.供电可靠性、电能质量与服务体验的提升，以及各种分布式绿色能源的消纳、电动汽车与灵活负荷的接入、多主体间的市场交易互动等，都需要通过配电系统来完成[1].然而，据统计 80%以上的用户停电事故是由配电网故障引发[2].因此，配电系统需要具备应对各种复杂不确定性故障的能力，以满足用户对电力供应的需求.负荷供电恢复作为提升配电网供电可靠性的核心手段之一，对于满足用户优质电力供应需求具有重要意义[3-4].考虑到配电系统中源、储、荷具有不同的运行特性，在系统安全运行的基础上，保障重要负荷的最大供电恢复水平，具有重要的科学意义和工程价值.

间歇性分布式电源的不确定性给配电系统的负荷恢复问题带来了极大的挑战，甚至导致供电恢复策略失效[5-6]，储能系统通过充放电可以在时间上进行能量转移[7]，从而有效降低由于分布式电源出力间歇性和随机性所带来的影响[8-9].通过协同储能系统与分布式电源的供电恢复策略，可以尽可能地扩大供电恢复范围，保障高优先级负荷的持续供电.

但由于储能系统和分布式电源的容量有限，难以对全部失电负荷进行供电恢复，与网络重构协调配合，可以进一步实现负荷恢复水平的提高.

目前，供电恢复和孤岛划分作为负荷恢复的主要手段多以恢复量最大为目标函数[10-11]，同时考虑负荷优先级等因素.传统的供电恢复手段以网络重构为主，负荷恢复模型多以描述系统潮流约束、网络拓扑约束为基础，孤岛划分模型还需满足岛内功率平衡约束.国内外已经开展了针对有源配电网负荷恢复问题的研究.文献[11]采用网络重构改变拓扑结构进行供电恢复，并通过鲁棒优化保证分布式电源和负荷出力波动时供电恢复策略的有效性；文献[12-15]采用恒定的负荷值和分布式电源出力值，利用启发式搜索算法寻找最优的孤岛划分策略；在极端故障情况下，文献[16]采用基于生成树的网络重构方法，采用分布式电源为失电负荷供电；为了进一步提升系统负荷恢复水平，文献[17]提出了一种采用可控分布式电源形成微电网进行供电恢复的方法.已有的负荷恢复方法大多忽略了源、储、荷的时序运行特性，难以保障配电网在持续运行中的功率平衡，并且需要根据负荷所在区域是否全部失电，选择供电恢复或孤岛划分方法，不能将两者统一建模求解.

本文提出了一种有源配电网多时段负荷恢复方法，首先，建立了一种基于源储荷运行特性的有源配电网多时段负荷恢复模型，考虑可控分布式电源、储能系统的控制模式影响，将供电恢复与孤岛划分问题统一建模；其次，为提高求解效率，采用凸松弛技术将负荷恢复模型转化为二阶锥规划模型；最后，在IEEE 33节点算例上验证了本文提出的负荷恢复方法在不同故障场景下的有效性.

1 有源配电网多时段负荷恢复模型

当配电系统由于故障而需要调整其运行方式时，若将不同时段的分布式电源出力及负荷水平视为某一恒定参数值求取故障恢复策略，则往往导致结果过于保守，不仅限制了有源配电网的负荷恢复能力，具有一定的运行风险.有源配电网多时段负荷恢复模型根据配电网发生故障的时刻，充分考虑了分布式电源、储能系统和负荷的时序运行特性，最大限度地保证了故障期间有源配电网内重要负荷的持续稳定运行.

在故障情况下，可控分布式电源及储能系统能够作为孤岛运行区域内的源节点为失电负荷提供电压/功率支撑[18].当分布式电源或储能系统被选作孤岛区域内的源节点时，应采用 V/f模式进行控制；而其余的分布式电源及储能系统则被视为普通负荷节点，采用 PQ控制模式.除考虑分布式电源、储能系统等的控制模式外，有源配电网多时段恢复模型还应考虑有源配电网运行约束以及各类型调节手段运行约束等[19]，具体模型如下所示.

1.1 目标函数

有源配电网多时段负荷恢复模型以配电系统故障期间负荷恢复量最大为目标函数，表示为

式中：Ωt为配电系统负荷恢复状态下的时间段面集合；Ωn为配电网节点集合；λi为节点 i的恢复系数，λi∈{0，1}，λi＝1 表示节点上负荷恢复，λi＝0 表示节点上负荷未恢复；Pt,iLOAD为节点i在时间断面t上的有功负荷.

1.2 配电系统辐射状运行约束

式中：Ωb表示配电系统支路集合；Ωs表示配电系统进行负荷恢复时，失电区域的电压和频率的节点集合；αij表示支路 ij的开断状态，αij＝1开关闭合，αij＝0开关断开；βij表示节点i和节点j的关系，βij＝1表示节点j是节点i的父节点，否则βij＝0.

各类型调节手段的控制模式选择可基于辐射运行约束实现，若式满足时，节点 i处调节手段采用V/f控制方式，否则采用PQ控制方式.

1.3 分布式电源运行约束

(1) 不可控分布式电源运行约束为

(2) 可控分布式电源运行约束为

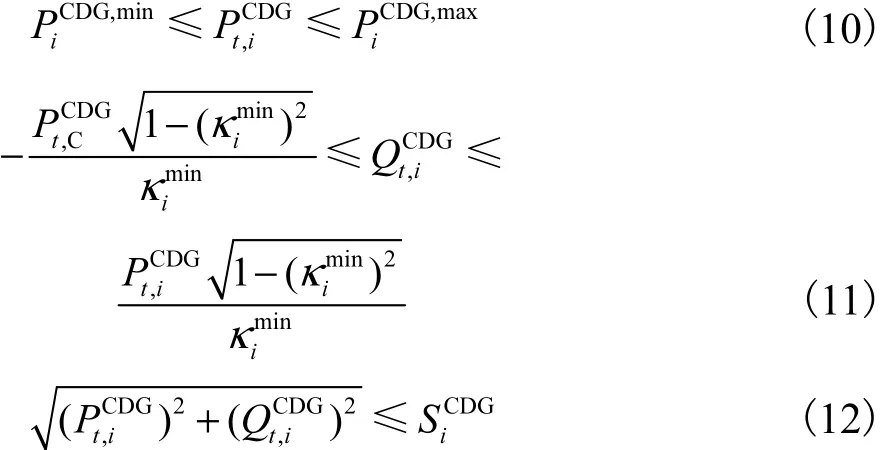
1.4 储能系统运行约束

1.5 系统潮流约束

系统潮流约束采用 DistFlow支路潮流形式进行描述[20]，表示为

式中：It,ij为时间断面t内节点i流向节点j的电流幅值；Ut,i为 t内节点 i的电压幅值；Rij为支路 ij的电阻；Xij为支路 ij的电抗；Pt,ij、Qt,ij分别为时间断面 t内支路 ij传输有功功率和无功功率；Pt,i、Qt,i分别为时间断面t内节点i的有功功率和无功功率；分别为时间断面 t内节点 i上负荷消耗的有功功率和无功功率.

配电网运行方式的调整需要通过分段/联络开关的开断改变网络拓扑结构，则式(22)可进一步转化为

式中 M 表示一个极大的常量.对于一个断开的支路，αij＝0，根据式(24)～式(26)可知，Pt,ij＝Qt,ij＝It,ij＝0，对于闭合的支路，αij＝1 时，式(27)和式(28)等价于式(22).

1.6 系统安全约束

(1) 运行电压约束为

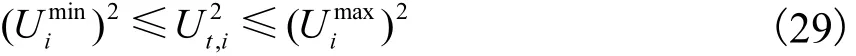
(2) 支路容量约束为

综上所述，得到有源配电网多时段负荷恢复模型.

2 凸松驰处理

考虑到有源配电网多时段负荷恢复模型的非凸非线性数学本质，本文基于其进行凸松驰处理[21].

对有源配电网多时段负荷恢复模型中的二次项和乘积项进行线性化，采用变量ut,i和it,ij替换，上述公式中节点电压和支路电流的平方项得

然后根据二阶凸松弛技术的基本原理，将式(9)、式(12)、式(13)、式(15)进行旋转锥约束转化得

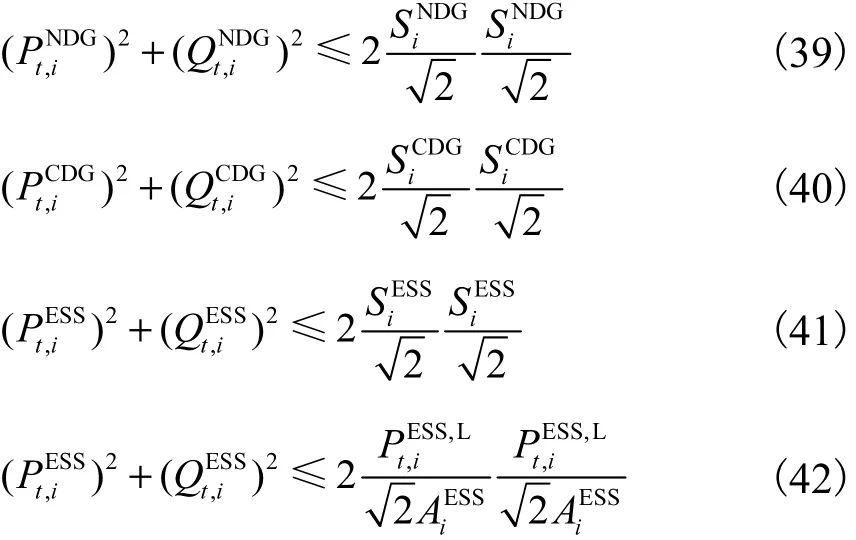
松驰式(33)得

进一步转化为二阶锥约束得

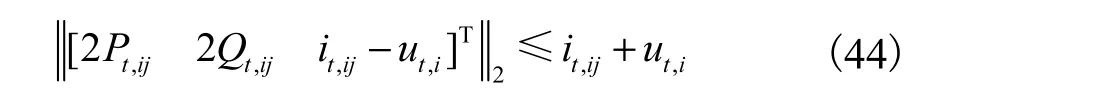
经过以上步骤，有源配电网多时段负荷恢复模型由难以高效求解的混合整数非线性规划模型转换为二阶锥规划模型，可调用已有成熟的数学优化工具CPLEX、MOSEK等进行求解.其具体求解流程如图1所示.

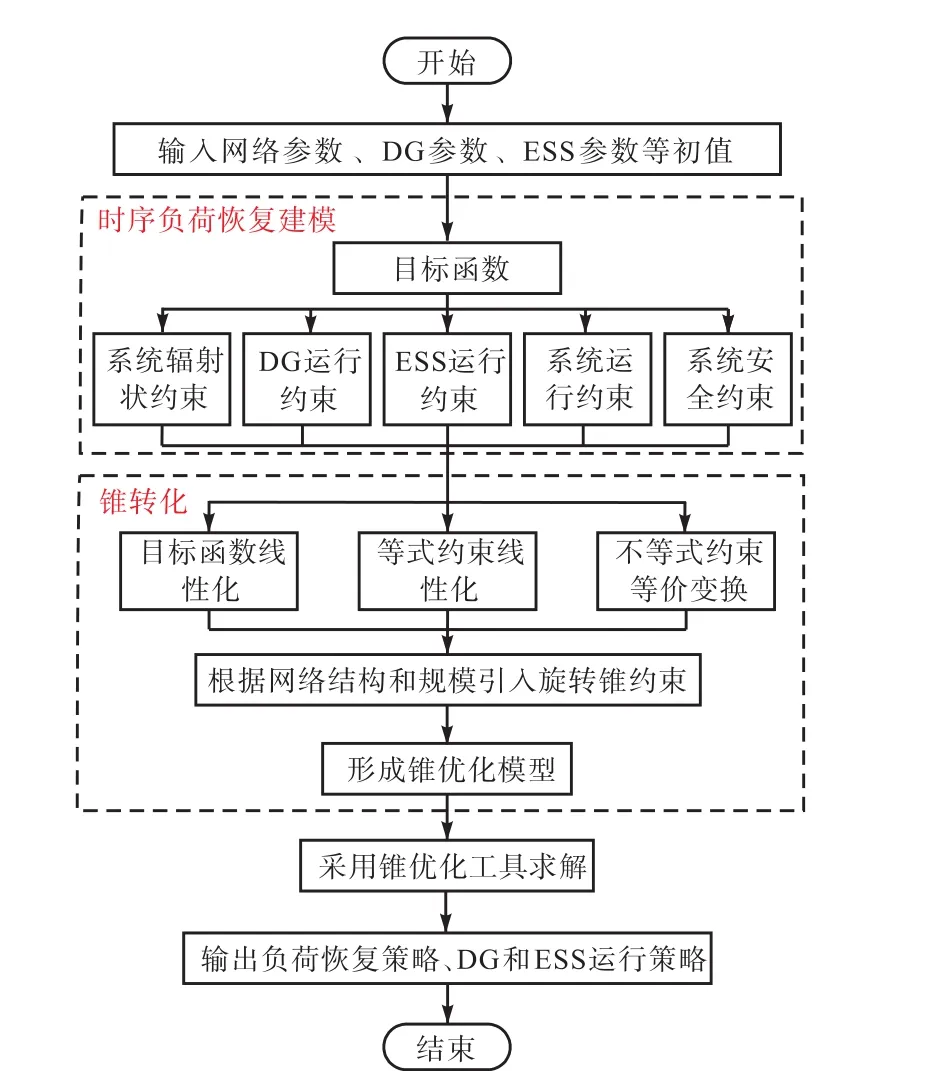
图1 多时段负荷恢复方法流程Fig.1 Flow chart of the proposed method

为分析该模型寻优结果的准确性，松弛偏差计算公式为

当gap小于可接受的误差精度，可以认为相应的最优解满足实际求解需求.

3 算例测试与分析

3.1 算例介绍

采用改进的 IEEE 33节点算例对本文方法进行分析测试，算例结构如图 2所示[22]。在算例中接入 6组光伏系统，容量均为 300kV·A；接入 5组可控分布式电源，容量为 300kV·A；各分布式电源功率因数均为 0.9。系统中储能接入情况如表 1所示。光伏及负荷的时序运行曲线分别如图3和图4所示[23]。

图2 IEEE 33节点算例Fig.2 IEEE 33-node test feeder

图3 光伏发电系统预测曲线Fig.3 Operation curves of the PVs

3.2 算例1

假定06:00时在支路1-2之间发生故障，失电范围为节点 2～33，总失电负荷为 3715kW，持续时长4h。设置如下4种场景进行对比，以验证本文方法的有效性。

场景1：采用分布式电源进行负荷恢复.

场景2：采用分布式电源和网络重构配合进行负荷恢复.

场景3：采用分布式电源和储能系统配合进行负荷恢复策略.

场景4：采用分布式电源、储能系统和网络重构进行负荷恢复.

极端故障情况下，有源配电网进入孤岛运行模式为重要负荷提供功率支撑.各场景孤岛运行结果如图5～图 8所示，孤岛区域由灰色阴影表示，负荷恢复节点由实心节点表示，失电负荷由空心节点表示.若可控分布式电源/储能系统被选为孤岛区域内的源节点，由绿色实心矩形表示，其控制策略为 V/f控制；P/Q控制策略下的分布式电源/储能系统则由绿色空心矩形表示.负荷恢复情况和各调节手段控制模式分别如表2和表3所示。各调节手段运行策略见图9～图16.

相比场景 1，将网络重构作为恢复恢复手段后，场景2中负荷恢复比例提升了4.3%；场景3中储能系统通过在时间维度对功率的调节，使得负荷恢复比例进一步提高了 12.9%；场景 4中负荷恢复比例最高，通过多类型调节手段协调配合可以进一步提升系统的供电恢复水平.

表1 储能系统配置参数Tab.1 Parameters of the ESS

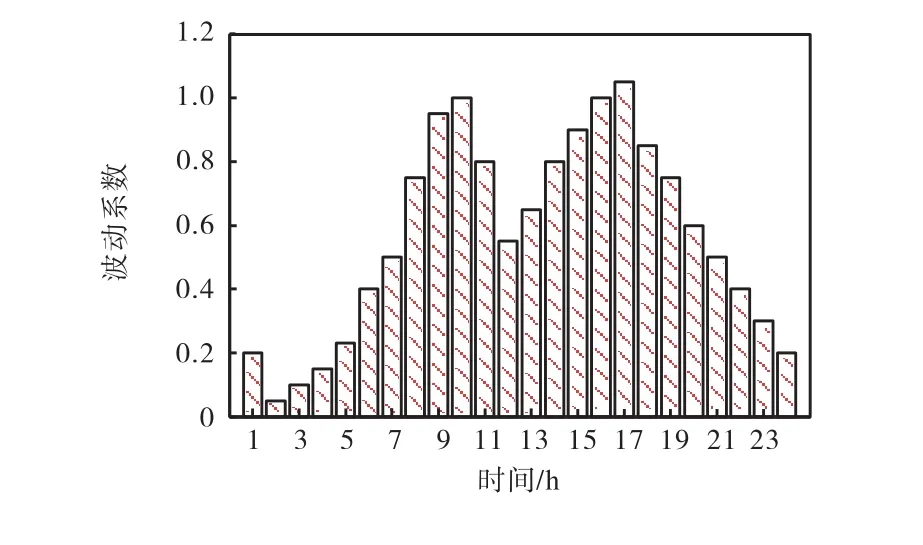
图4 负荷预测曲线Fig.4 Operation curves of the loads

图5 场景1负荷恢复情况(算例1)Fig.5 Load restoration under scenario 1(case 1)

图6 场景2负荷恢复情况(算例1)Fig.6 Load restoration under scenario 2(case 1)

图7 场景3负荷恢复情况(算例1)Fig.7 Load restoration under scenario 3(case 1)

图8 场景4负荷恢复情况(算例1)Fig.8 Load restoration under scenario 4(case 1)

表2 4种场景下负荷恢复情况(算例1)Tab.2 Load storation under the four scenarios(case 1)

图9 场景1下可控分布式电源和光伏发电系统出力Fig.9 Output power of controllable DGs and PVs in scenario 1

图10 场景2下可控分布式电源和光伏发电系统出力Fig.10 Output power of controllable DGs and PVs in scenario 2

图11 场景3下可控分布式电源和光伏发电系统出力Fig.11 Output power of controllable DGs and PVs in scenario 3

表3 可控分布式电源控制模式Tab.3 Operation strategies of controllable distributed generators

图12 场景3储能系统充放电功率Fig.12 Output power of ESS in scenario 3

图13 场景3储能系统荷电状态Fig.13 State of charge in scenario 3

图14 场景4下可控分布式电源和光伏发电系统出力Fig.14 Output power of controllable DGs and PVs in scenario 4

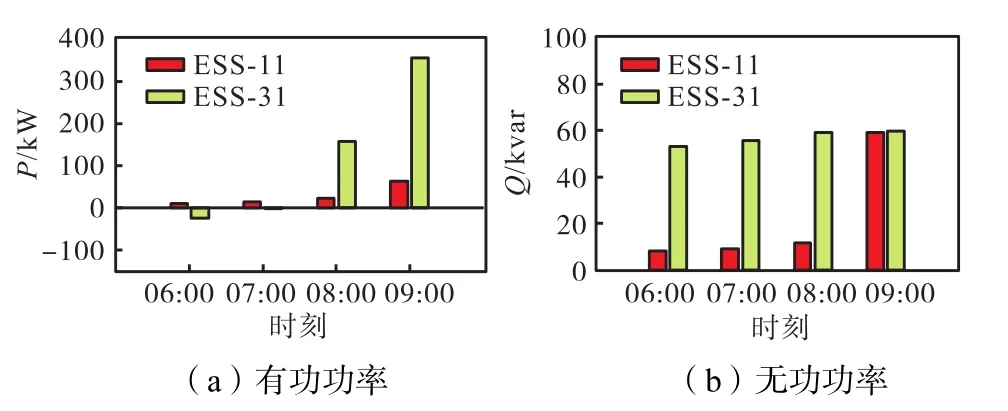
图15 场景4储能系统充放电功率Fig.15 Output power of ESS in scenario 4

图16 场景4下储能系统荷电状态Fig.16 State of charge in scenario 4

3.3 算例2

假定06：00时在支路2-3之间发生故障，故障点下游负荷节点 3～18和节点 23～33全部失电，持续时长 4h.设置如下 4种场景进行对比，以验证本文方法的有效性.

场景1：采用联络开关进行负荷恢复.

场景2：采用网络重构进行负荷恢复.

场景3：采用储能系统和联络开关进行负荷恢复.

场景4：采用储能系统和网络重构进行负荷恢复.

当负荷所在区域部分失电时，有源配电网调整至供电恢复模式进行负荷恢复.负荷恢复结果如图17～图20所示，负荷恢复情况如表4所示.

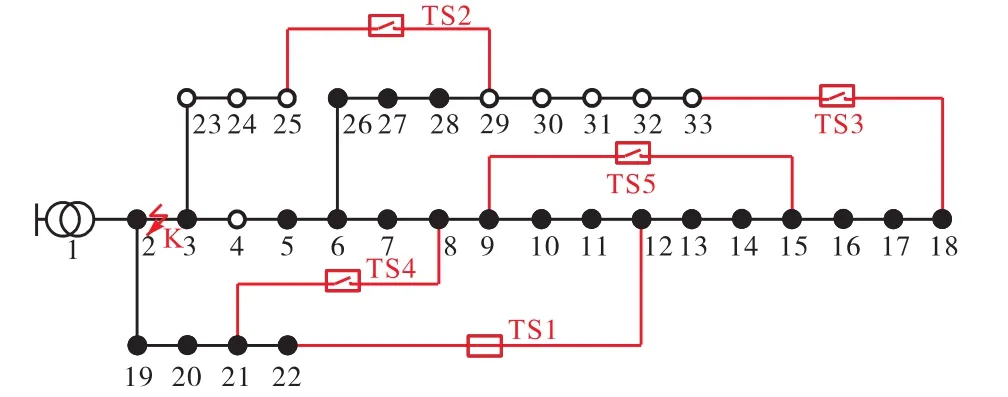
图17 场景1负荷恢复情况(算例2)Fig.17 Load restoration under scenario 1(case 2)

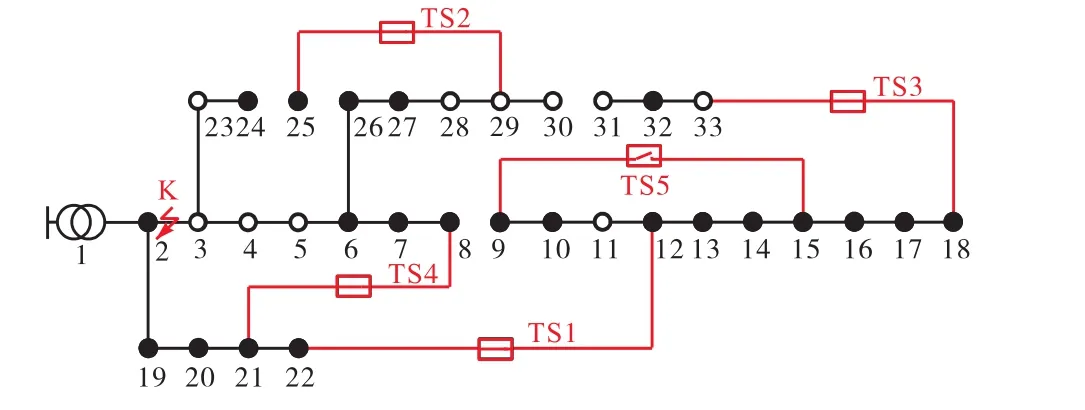
图18 场景2负荷恢复情况(算例2)Fig.18 Load restoration under scenario 2(case 2)

图19 场景3负荷恢复情况(算例2)Fig.19 Load restoration under scenario 3(case 2)

图20 场景4负荷恢复情况(算例2)Fig.20 Load restoration under scenario 4(case 2)

对比场景1和场景4，储能系统及网络重构能将负荷恢复量提升34.7%，显著提高了配电系统负荷恢复水平.可以看出，本文提出的方法不仅能够在负荷所在区域完全失电时，通过孤岛运行模式提升配电系统负荷恢复水平，也能在部分失电的情况下，通过供电恢复策略，提高配电系统恢复供电比例.

表4 4种场景下负荷恢复情况(算例2)Tab.4 Load recovery under the four scenarios(case 2)

4 结 论

(1) 充分考虑光伏、风电等间歇性分布式电源的时序特征，建立了有源配电网多时段负荷恢复模型，将供电恢复与孤岛划分统一建模，数学本质上属于混合整数非线性规划问题.

(2) 采用二阶锥模型转化，实现了有源配电网多时段负荷恢复模型的高效求解.

(3) 基于改进的IEEE 33节点算例，设置不同的故障场景，以验证本文方法的有效性.

(4) 通过实现多类型负荷恢复手段的协调配合，有效应对系统的多种故障场景，以实现重要负荷的持续供电，从而大幅提升系统负荷恢复水平及供电可靠性.