基于深度增强学习的卫星姿态控制方法

西安微电子技术研究所，西安 710065

良好的姿态控制方法对空间卫星的稳定在轨运行至关重要。卫星在轨运行中，由于燃料的长期消耗、载荷的在轨捕获与释放(如从宇宙飞船上释放卫星,捕获目标、清除轨道垃圾等)、与其他航天器的对接等，且星体本身具有非线性、高阶、时变等特性[1]，都会导致系统的运动状态及质量特性发生变化，且很多变化是剧烈的(如捕获、释放卫星,与目标的对接等)、无法确知的(如对非合作目标的操作、轨道垃圾的清理等)[2]。现有的姿态控制算法大部分依赖被控对象的质量参数(包括质量、转动惯量等)，需要通过各种手段辨识其质量参数，此种情况下难以给出准确的参数辨识[3-4]，且此类系统动力学模型复杂，具有较强的非线性，容易导致现有的姿态控制系统失效[5]。因此,迫切需要一种高自主的具备高度智能化程度的姿态控制技术，解决传统控制难以对付的航天器质量特性在轨变化情况下的航天器高性能控制问题。

目前，卫星姿态控制的实际问题是外部干扰、转动惯量的不确定性和模型的非线性问题[6]。针对此类复杂情况下的姿态控制问题，文献[7]基于Backstepping法，设计能解决转动惯量不确定的自适应控制律，可以解决系统Lyapunov函数构造困难的问题。Yoon等人针对航天器姿态控制中存在惯量的不确定性，提出了一种非线性哈密顿MIMO系统新型控制律[8]。Queiroz等人利用完整系统的动力学模型设计了非线性自适应控制，证明了在干扰为未知量的情况下闭环系统的跟踪误差全局渐进收敛[9]。苗双全利用一种自适应滑模控制策略解决了大型挠性航天器机动过程中出现的振动问题[10]。总的来看，目前面向空间飞行器姿态控制的算法智能化程度低，且通常都是针对具体应用进行设计，不具备普适性。所以，随着航天探索任务复杂程度的不断提高，需要设计一种具备高度智能化程度的姿态控制技术。

深度增强学习是直接从高维原始数据学习控制策略的一项技术[11]，为了解决从感知到决策的计算机控制问题，从而实现通用人工智能。它在过去两年中得到了迅速发展，并在视频游戏和机器人领域取得了突破性进展[12]。而DQN(Deep Q Network)是深度增强学习的典型算法之一，它将神经网络和Q-Learning结合起来，输入是原始图像数据，输出则是每个动作对应的价值评估(Q值)[13]。2013年Google公司的DeepMind团队在NIPS的深度学习研讨会上提出DQN算法[14]，在Atari游戏平台展示了此类算法在智能决策方面的巨大应用潜力。

本文拟采用深度增强学习算法，针对空间卫星智能姿态控制问题，提出一种通过自主学习实现卫星智能姿态控制的方法，突破现有方法被控对象依赖复杂动力学模型和严格质量参数的局限，解决遭遇突发随机扰动的卫星姿态不稳定问题，提高姿态控制算法的姿态稳定度和控制精度。

1 姿态控制方法

本文将卫星智能姿态控制问题定义为：轨道坐标系上保持稳定姿态角速度运转的空间卫星，在遭遇突发扰动姿态发生变化后，如何操作控制力矩以稳定卫星的姿态为初始状态。已有的传统解决方法PD控制器由于依赖严格的质量参数条件，往往使得输出的姿态角速度发散。为此这里使用深度增强学习技术解决这一问题，过程分为如下两步：1)搭建随机扰动下控制力矩与姿态角速度互相反馈的动力学环境；2)使用DQN算法进行控制力矩的深度增强训练。设计流程如图1所示。

图1 基于深度增强学习的卫星姿态控制方法示意Fig.1 Sketch map of satellite attitude control method based on deep reinforcement learning

1.1 动力学环境搭建

为了研究卫星姿态控制问题，本文基于空间卫星的动态特性建立了轨道坐标系; 也就是说，坐标原点位于卫星的质心，Z轴指向地球中心，Y轴位于卫星轨道平面的负法线，X，Y和Z轴构成一个右手系统。 同时为描述卫星姿态在力矩作用下的运动情况，需建立正确的姿态动力学和运动学模型[15]。

(1)建立姿态动力学模型方程

卫星的动力学模型由单刚体的欧拉动力学方程描述如下：

(1)

式中：T为作用于刚体质心上的控制力矩;I为刚体的转动惯量矩阵;ω=[ωxωyωz]T为刚体的姿态角速度。若已知姿态角速度的初值为ω0，给定控制力矩T，将I设为定值，则能够通过积分式(1)得到任意时刻卫星的姿态角速度。

(2)建立姿态运动学模型方程

由于卫星的姿态可通过姿态四元数来表征。下式为卫星基于四元数的姿态运动学方程，ω=[ωxωyωz]T为卫星的姿态角速度，若已知卫星在初始时刻的姿态四元数为Q0，则可通过积分表示卫星在任意时刻的姿态。

(2)

(3)搭建动力学环境

搭建动力学环境过程如下：

第1步，初始化卫星的姿态角速度ω0及姿态四元数Q0；

第2步，给定一个随机扰动力矩Tr，设定周期为I；

第3步，依次对式(1)(2)积分，求解第i(i=1,…,I)个周期内的姿态角速度ωi及姿态四元数Qi，循环输出整个周期的姿态(ω,Q)；

第4步，以(ω,Q)作为卫星的初始姿态输入到神经网络中，返回至第3步，不断循环。

作为对比，引入PD控制的方法，同样以此向量作为卫星的初始姿态输入到PD控制器中，输出控制力矩。

1.2 深度增强训练

本节在动力学环境的基础上，以卫星姿态为输入，使用DQN算法智能输出卫星的控制力矩[16]，并送入动力学环境中获得卫星姿态，继续输入到神经网络中训练权重。

(1)离散化控制力矩的连续输出

DQN是一个面向离散控制的算法，即输出的Action是离散的，无法输出连续的Action，因为Q值的更新需要通过求最大的Action来实现。然而在要解决的卫星控制问题中，控制力矩的输出是连续高维的，无法使用传统的DQN解决，故此处对输出的控制力矩进行离散化。

卫星的控制力矩是一个三维向量T=[TxTyTz]T，设定控制力矩中每一个方向分量的取值范围，如Tx∈[ax,bx]，Ty∈[ay,by]，Tz∈[az,bz]，分别等分Tx、Ty、Tz为5等份，为每一份设置标志向量，分别为[1 0 0 0 0]、[0 1 0 0 0]、[0 0 1 0 0]、[0 0 0 1 0]、[0 0 0 0 1]，以此向量代表控制力矩进行Q值迭代。

(2) 定义reward函数及终止条件

深度增强训练的目标是输出卫星的控制力矩，使得卫星的姿态角速度与期望姿态角速度之间的误差越来越小，衡量的标准是得到尽可能多的回报，因此奖励(reward)函数需要具有角速度差值(定义为error)越小，reward越大的性质，适用的高斯函数如下：

(3)

前述DQN算法中提到了训练中需要设置任务的终止条件，要为每一次输出的控制力矩进行是否完成任务的判断，即此力矩能否使卫星姿态恢复稳定。此处根据卫星姿态角速度的取值范围，定义每次迭代姿态角速度与期望姿态角速度之间的误差处于某个确定范围时，任务继续训练，反之任务终止。

(3) 神经网络训练流程

本文使用两层的全连接神经网络，以卫星当前的姿态角速度和姿态四元数作为输入，输出一个数值指示控制力矩大小的概率。与卷积神经网络不同，每个神经元仅连接到少量神经元[17]，全连接神经网络连接到上层的所有神经元。综上，基于DQN的深度增强训练流程如下：

1)初始化经验池D的容量为N，用于存储训练的样本。

2)用一个深度神经网络作为Q值网络，初始化权重参数θ。

3)设定控制任务训练总数M，初始化网络输入状态x1，并且计算网络输出a1。循环开始：

②在环境中执行at后，得到奖励rt和下一个网络的输入xt+1；

③将4个参数(xtatrtxt+1)作为此刻的状态一起存入D中(D中存放着N个时刻的状态)；

④当D积累到一定程度，每次执行完①～③步后再随机从D中取出minibatch个状态；

⑤计算每一个状态(xjajrjxj+1)的目标值yj=

⑥通过SGD更新网络权重参数，使用均方差定义损失函数[yj-Q(xj,aj;θ)]2,返回①，循环执行，不断训练模型。

4)多次训练，获得模型。

2 仿真试验

为验证所提出方法的有效性，本节进行了仿真试验。首先利用动力学模型模拟卫星在太空中的运动状态，然后为模拟卫星执行的目标捕获或载荷释放等任务，在上述动力学模型的基础上对卫星施加一个随机扰动力矩，并同时随机改变转动惯量以模拟卫星质量参数变化。所提出的方法应在此状态下不断输出控制力矩，以控制卫星恢复稳定的飞行姿态。

具体来说，定义随机扰动力矩Tr=10-8×[0.5 -0.5 0.5]T×r，其中r为随机数。初始化卫星的姿态角速度ω0=[0.001，0.001，0.001]Trad/s及姿态四元数Q0=[1 0 0 0]T。姿态控制算法在此扰动后，不断输出控制力矩，使卫星的姿态角速度能够收敛到一定值，且此值与期望姿态角速度ω0之间的误差趋于零时，说明姿态控制算法具有有效性。作为对比，本文同样仿真基于PD控制器的传统姿态控制方法，并输出了控制结果。算法在Anaconda3软件包和TensorFlow深度学习软件框架的基础上实现。

2.1 基于PD控制器的姿态控制

PD控制器严格依赖于被控对象的质量参数即转动惯量I，当I随机取一定值时，卫星遭遇干扰后迭代30次的姿态角速度及其误差如图2所示。图2表明，随着迭代次数的增加，姿态角速度与期望姿态角速度的误差均逐渐增大未能收敛，这一发散的姿态角速度误差表明卫星不能保持姿态稳定。

2.2 基于DQN训练的姿态控制

定义循环次数为3 000，训练前观测的时间步为1 000，经验池的容量为500，观测的衰减率为0.99，将遭遇干扰的动力学模型作为环境，转动惯量矩阵随机取值，进行基于DQN算法的深度增强训练。每迭代100次记1次卫星的姿态角速度及误差向量，并展示其迭代3 000次的变化趋势如图3～图5所示。

图2 姿态角速度及其误差的发散曲线Fig.2 Divergent curve of the attitude angular velocity and its error

图3 姿态角速度及其误差的x分量变化曲线Fig.3 Varying curve of attitude angular velocity and its error of x

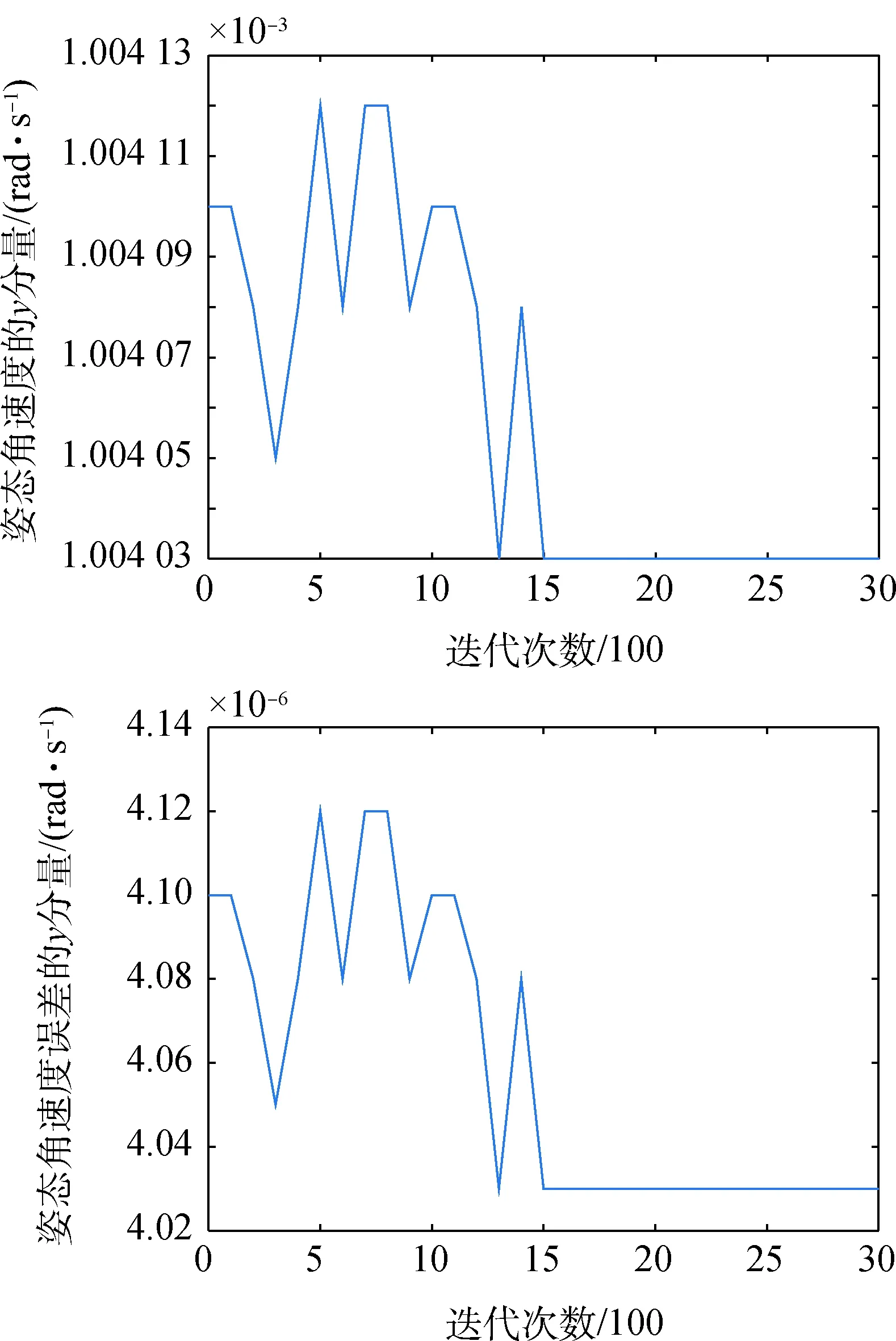
图4 姿态角速度及其误差的y分量变化曲线Fig.4 Varying curve of attitude angular velocity and its error of y

图5 姿态角速度及其误差的z分量变化曲线Fig.5 Varying curve of attitude angular velocity and its error of z

姿态角速度3个方向分量的变化曲线表明，随着迭代次数的增加，卫星的姿态角速度收敛于[0.000 985 37，0.001 004 03，0.001 002 19] rad/s，与期望姿态角速度的误差收敛于[1.463 389 90×10-5，4.029 654 22×10-6，2.192 512 30×10-6] rad/s，误差变化曲线表明，3个分量的值均减小并收敛，说明卫星姿态达到稳定状态，基于DQN的姿态控制方法具有有效性。与图2的对比也验证了这一算法在随机参数变化下仍具有稳定卫星姿态的性能优势。

每迭代100次记录1次reward的平均值，并绘图如图6所示。由图6可以看出reward函数遵循减函数的性质，从快速提升到基本达到了高峰，说明增强学习取得了最优决策。

图6 reward的变化曲线Fig.6 Varying curve of reward

综上，当转动惯量随机取值时，DQN能够获得控制力矩的最优智能输出，也即DQN并不依赖于被控对象的质量参数，能够在卫星受到突发的随机扰动后自主地对卫星姿态进行稳定，可以解决传统的PD控制器无法解决的复杂任务中的卫星姿态稳定问题。

然而，本文提出的姿态控制方法的系统稳定性目前还不能保证，尽管模拟的仿真动力学环境中能够很好地在卫星受到突发随机扰动后控制卫星的姿态，但真实星上环境复杂，干扰众多，计算资源有限，在模拟环境中训练好的智能体还不能直接应用于真实空间环境中的星上姿态控制，还需要进一步模拟更加完善的空间环境，以便进一步训练更好的智能体，从而保证系统的稳定性。

3 结束语

本文提出的基于深度增强学习的卫星姿态控制方法是一种基于学习(训练)的方法，学习阶段是在地面上进行的。在学习阶段之后，获得一个训练好的神经网络模型作为智能体，直接将其应用于卫星，智能体将充当大脑来控制仿真动力学环境中的卫星的飞行姿态。在本文中，训练好的智能体的有效性在仿真动力学环境中已经得到了验证。

目前仅在仿真动力学环境中验证了本文所提方法的有效性，还未开展应用于星上的研究，暂未考虑快速性。下一步的工作，计划搭建地面半实物仿真试验系统，利用二维伺服转台模拟卫星在轨飞行真实姿态，仿真过程中将传感器(陀螺仪、加速度计等)安装在转台上以采集控制系统所需输入信息，以伺服控制技术模拟控制器输出，从而对在动力学仿真环境中提出的姿态控制方法进行训练和测试。待到智能体训练得足够好时，最终将训练好的智能体直接应用于星上，根据卫星当下的姿态在线实时得到控制序列，并作用于卫星的发动机上，达到控制卫星姿态的目的。