单星测频静态目标无源定位研究
2019-10-15
北京遥感信息研究所,北京 100192
随着通信电子技术的迅速发展,探测定位技术的应用越来越广泛,特别是在军事斗争中的地位和作用不断提高。在越来越强调隐蔽攻击的趋势下,传统的有源探测定位技术暴露出隐蔽性差、截获率高的弱点。因此,采用被动方式工作的无源探测定位技术越来越受到重视,正逐渐成为定位方法发展的主流[1-5]。它比有源探测定位方法具有作用距离远、宽带工作、低截获概率等优点,是现代电子对抗中不可缺少的重要手段,同时在航海、航空、宇航、侦察、测控、救援和地球物理学中也扮演着重要的角色。
在星载无源定位系统中,常采用干涉仪测向或时差方法对地面辐射源进行定位。干涉仪测向定位利用一颗卫星即可实现对地面干扰源进行定位,算法简单,但是天线结构复杂,需要解相位模糊,测向通道的相位一致性要求也较高,并且由于受测向精度的限制,定位误差一般为几十千米。时差定位需要多颗卫星才能进行定位,技术比较复杂,成本较高,对卫星星座时统的一致性要求非常高,在工程应用中实现难度较大[6-8]。
单星测频定位技术利用观测平台和目标之间相对运动所产生的多普勒频率对辐射源进行定位。对于地面辐射源,一颗卫星通过对同一地面目标进行4次测量就可确定辐射源的位置。由于低轨卫星的移动速度很快,产生的多普勒频率大,因而有利于定位精度的提高,而且单颗卫星降低了系统实现难度和发射成本,还可以通过多次测量来提高定位精度[9-10]。
本文首先分析了单星测频定位技术的基本原理,提出了基于非线性最优化技术的求解算法。然后,结合工程实际,探讨了数据测量、数据预处理技术和系统误差分离技术。最后通过一组仿真试验和多次实际应用验证了单星测频定位技术有效性。
1 单星测频无源定位方法
根据运动学原理,当侦察卫星与目标辐射源作相对运动时,这种相对运动可以分解为径向和切向两个分量,其中,径向运动分量将导致信号的瞬时频率存在多普勒频移现象,而多普勒频移又表征为卫星状态信息和辐射源目标位置参数的非线性函数[11-12]。因此,可以基于最优化技术求解非线性模型,从而实现对辐射源目标的定位与跟踪,如图1所示。

图1 星载测频定位原理Fig.1 Schematic diagram of passive localization of single satellite using frequency measurement
1.1 频率测量定位建模与最优化求解技术
假设侦察目标在地心固连坐标系中的位置可以表示为:
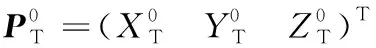
(1)
在卫星观测时间内,可以将目标的位置表示为一个3次多项式,即:

(2)

(3)

(4)
对于固定目标,在式(2)~(4)中,只取常数项,对于匀速运动目标,只取常数项和一次项,而对于匀加速运动目标只取常数项、一次项和二次项。
因此,目标和卫星之间的相对距离及其导数为

(5)
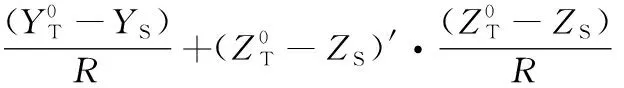
(6)
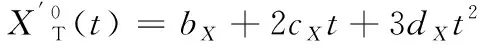
(7)

(8)
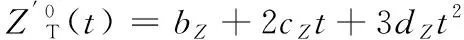
(9)
其中,卫星的位置和速度信息由GPS数据提供。
根据多普勒原理可知,侦收信号频率可表示如下:
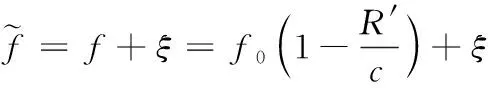
(10)
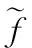
(11)
式(11)中的未知数只有目标的位置和速度信息。因此,可以基于梯度下降法最优化搜索策略,由式(11)可实现对目标的定位,构造如下最优化模型:

(12)
为了求解最优化模型(12),还需要确定搜索区域。对于测向定位体制,由于已经获得了初始定位点,因此,其搜索区域可以设为初始定位点附近。但是,如果没有初始定位点信息,则由于多普勒频移只与目标和卫星之间相对距离的变化率有关。因此,最优化模型(12)必然存在两种关于卫星轨道对称分布的最优结果,在没有其他信息的前提下,需要人工判定,舍弃其中的一个模糊点,保留真实的定位点。
为了提高最优化模型(12)估计精度和稳定性,还需要做一些相关处理工作。首先,由于式(2)~(4)中位置参数过多,会影响后续最优化求解,因此,为保证估计精度,需要进行降维处理。由于一般低速运动目标相对于卫星运动速度是可以忽略不计的,因此,可以基于固定目标情形来讨论。由于大地坐标系与地心固连坐标系的坐标转换为:

(13)
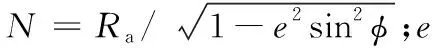
1.2 频率测量数据预处理技术
(1)野值点剔除
在卫星测量数据中,由于信噪比较低,会产生大量的野值点。这些野值点的特性不同于随机噪声,其幅度是远大于随机噪声的,而且分布不均匀,无规律,如果不将其剔除,会严重影响数据处理过程和定位精度。
对于野值点地剔除,已有大量文献对其进行了研究[5],并提出了许多相关技术手段和方法。几乎所有野值剔除方法都利用了野值点的一个重要特征,即野值点的跳跃性。一般情况下,野值点几乎无连续性和光滑性可言。因此,本平台也是以此特征作为突破口,采用函数逼近理论,剔除野值点,提取真实弱信号。
设测量数据为y(t),真实值为x(t),随机误差为ξ(t),野值点为δ(t),则有:
y(t)=x(t)+δ(t)+ξ(t)
(14)
将真实信号x(t)表征为一组正交基函数的线性组合,即

(15)
将式(15)代入式(14),则有
y(t)=H(t)·c+δ(t)+ξ(t)
(16)

图2 单星测频定位流程Fig.2 Flowchart of passive localization method of single satellite using frequency measurement
为了有效剔除野值点,首先需要正确识别野值点。若记E(t)=y(t)-H(t)·c,如果t时刻存在野值点,则E(t)将具有较大的方差,即
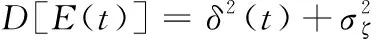
(17)
因此,可以基于式(17)识别t时刻是否存在野值点。
在实际应用中,可以事先设定一个阈值γ,则可以构造如下判断准则,判断t时刻是否存在野值点:

(18)
一般情况下,阈值γ≤3,即通常的3σ原则。
在式(18)中需要已知事先模型参数c和噪声方差σζ,而为了求得模型参数c,则必须首先识别出真实信号x(t)。由于野值点具有无规律的大幅度跳跃这一特性,而真实信号则是一个缓变的光滑信号,因此,可以基于测量信息y(t)的导数信息进行判断。
若令二阶差分:
Δy(t)=[y(t+Δt)-2y(t)+y(t-Δt)]/2Δt
式中:Δt为采样间隔。构造如下判断准则,判断t时刻是否真实信号:
(19)
式中:阈值ρ≤1。
由式(19)识别出真实信号后,若记存在信号的时刻为tI,则可得:
(20)
式中:HI=H(tI),yI=y(tI)。
将式(20)代入式(15),则有:
x(tI)=H(tI)·cI
(21)
从而可得:
E(tI)=y(tI)-x(tI)
(22)
由式(22)即可估计噪声方差σζ。
因此,基于式(18)~(22)可以有效剔除野值点和提取弱信号,试验中野值剔除前与剔除后对比如图3、图4所示。此外,如果经过上述处理流程,一次未能完全把野值点剔除干净,则可以将第一次处理后的测量信息作为新的测量信息,再按上述流程进行处理。经过这样几次循环迭代后,可以将野值点完全剔除干净。
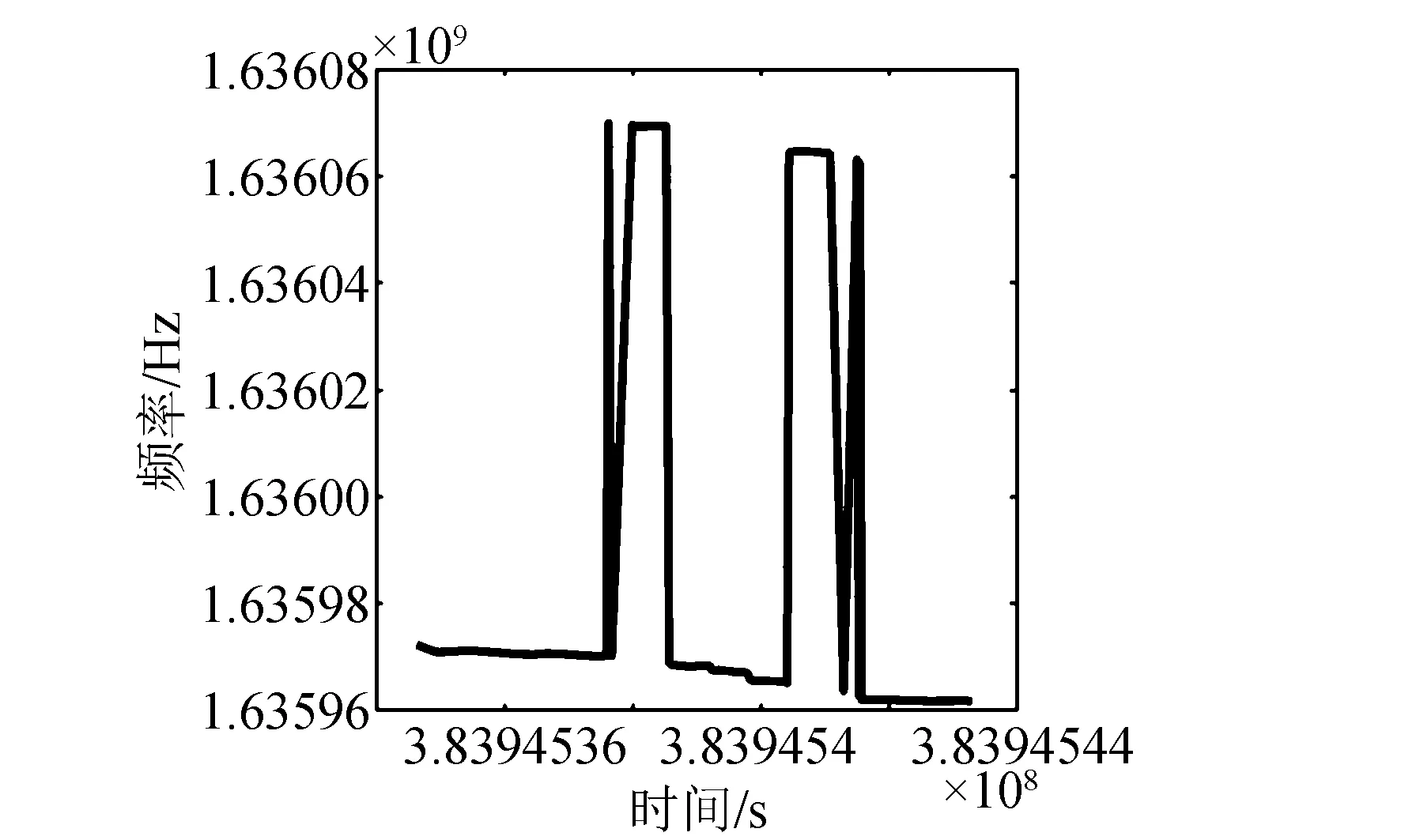
图3 野值点剔除前的频率Fig.3 Frequency distribution without outlier elimination
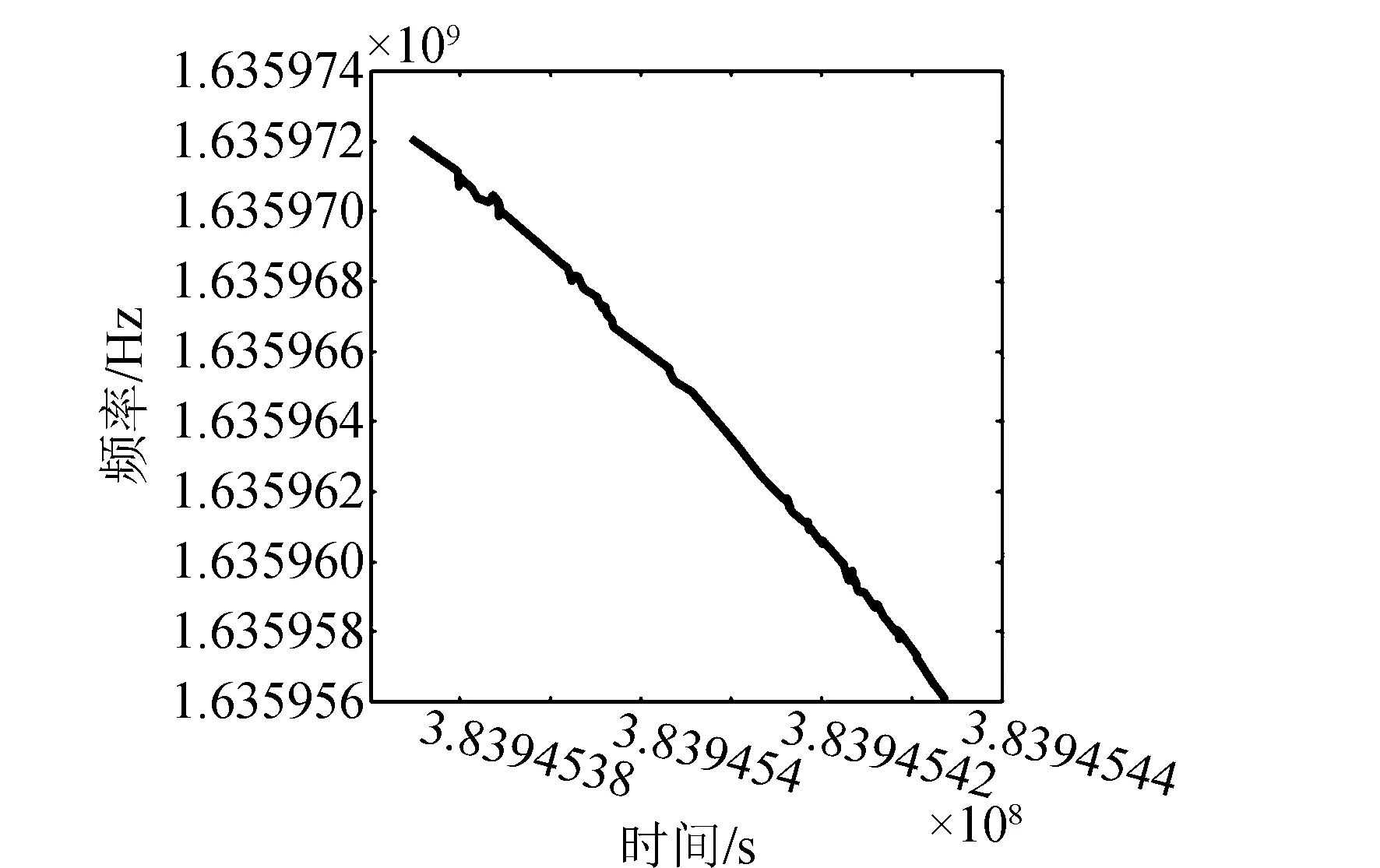
图4 野值点剔除后的频率Fig.4 Frequency distribution after outlier elimination
(2)随机误差平滑
在数据处理中,经常会碰到测量数据中的随机误差,这些随机误差在一定程度上会影响数据处理结果和精度,需要对其加以抑制和平滑。在目标定位与跟踪领域,较为传统的随机误差平滑技术是非线性滤波技术,比如扩展卡尔曼滤波、不敏卡尔曼滤波、粒子滤波和伪线性滤波技术等方法。这些滤波方法具有很好的时效性,但是,在迭代过程中,所有这些滤波方法[5]均只利用了当前时刻以前的测量信息,而当前时刻以后的信息则不参与运算,使得迭代过程有可能会发散和失真。
对于卫星辐射源定位领域,由于一般采用事后处理,而且在单星情况下是很难保证定位的实时性。因此,本平台采用函数逼近理论对随机误差进行平滑,这种方法可以有效地将全程数据进行融合处理,最大限度地利用测量信息。
假设测量数据为y(t),真实值为x(t),测量随机误差为ξ(t),则有:
y(t)=x(t)+ξ(t)
(23)
假设x(t)为一连续函数,则根据函数逼近理论,可以将x(t)表示为一组正交基函数的线性组合,即:
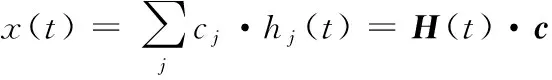
(24)
式中:hj(t)为一组正交基函数,一般可以选择多项式基、三角函数基和B-样条函数基等。将式(24)代入式(23),则有:
y(t)=H(t)·c+ξ(t)
(25)
因此,为了平滑随机噪声ξ,提取信号x(t),则只须求解式(25)中的模型参数c。若假设噪声ξ(t)是线性无关的,则根据最小二乘技术可得
c=(HT·H)-1·H·y
(26)
式中:y=y(t);H=H(t)。将式(26)代入式(25),则有
x(t)=H·(HT·H)-1·H·y
(27)
通过式(27)即可实现对随机误差的抑制和平滑,同时也可以有效的从测量信息y(t)提取真实信号x(t)。由于该方法利用了所有观测时刻的测量信息,使得信号估计结果能很好的与真实值吻合,而且可以通过调节基函数类型和参数,可以获得更优的估计结果,试验中原始数据经随机误差平滑处理后的效果如图5所示。
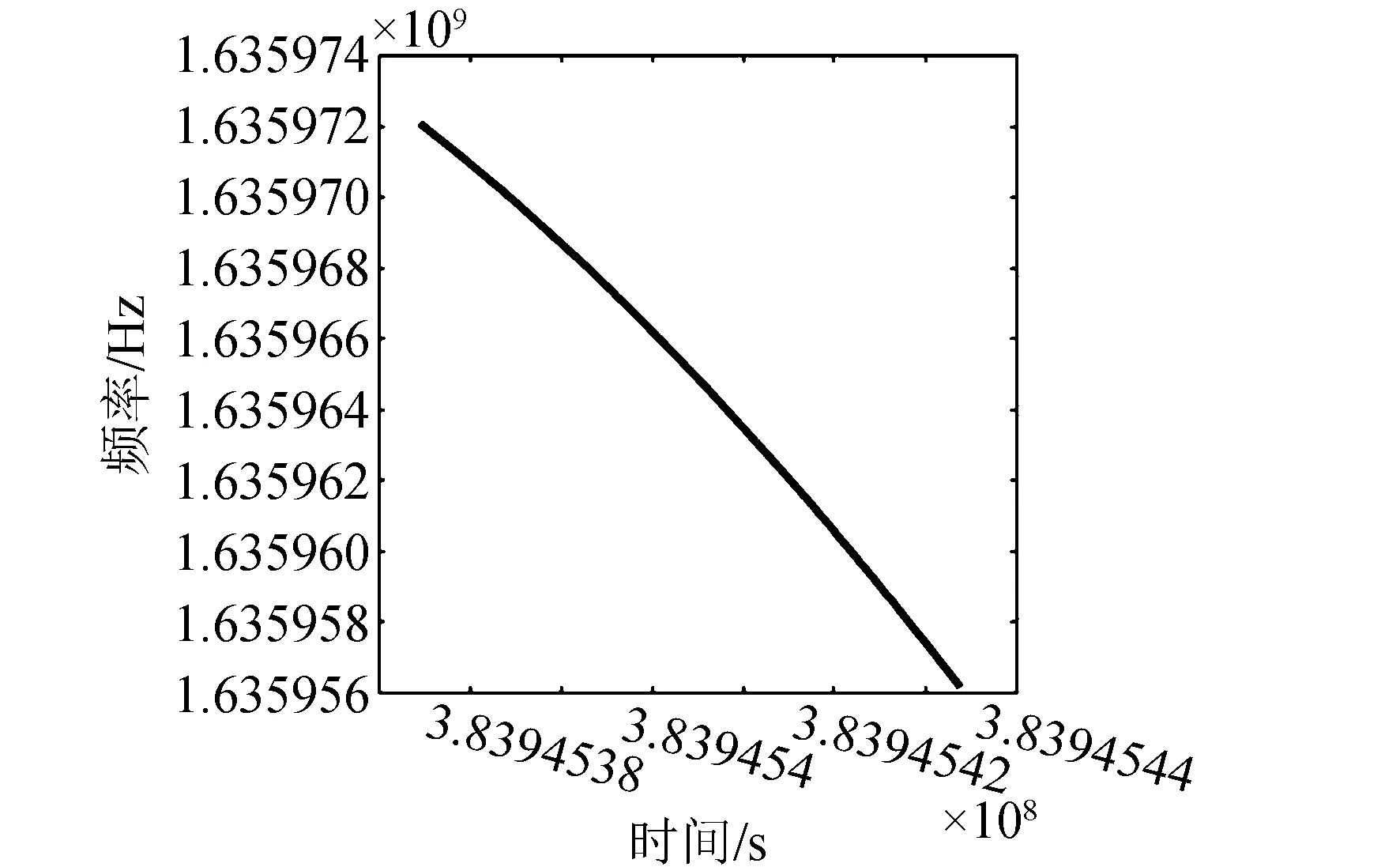
图5 平滑后的频率Fig.5 Frequency distribution after stochastic error processing
(3)频率测量数据系统误差建模与分离技术
由于受复杂电磁环境和接收机性能影响,星载频率测量值可用下式表征:
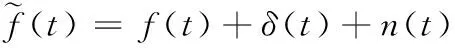
(28)
一般情况下,系统误差是一个随时间缓变的小量,可以用多项式函数来表征,即:
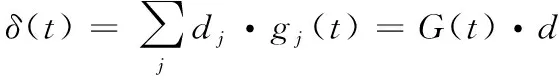
(29)
式中:gj(t)为多项式基函数;d为模型参数。
通过对实际侦收数据的分析,不同时刻的随机误差之间存在一定的相关性。根据时间序列分析方法,可以用自回归序列AR模型来表征随机噪声,即:
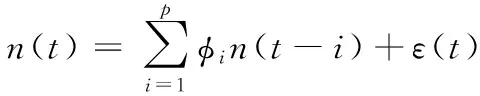
(30)
式中:p为模型阶数;φi为自回归系数;ε(t)为零均值高斯白噪声,且n(t)与ε(t)不相关。
引入后移算子B,即B·n(t)=n(t-1),则可将式(30)简化为:
Φ(B)·n(t)=ε(t)
(31)
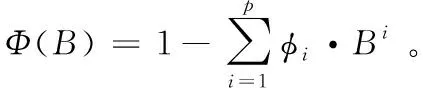
由式(28)~(31)可知,测量噪声

(32)
式中:n(t)为零均值平稳AR(p)序列;P为自回归序列AR模型阶数;r为多项式函数阶数。式(32)中所称为PAR模型(P为Polynomial的缩写)[4]。
将式(31)代入式(32),可得:
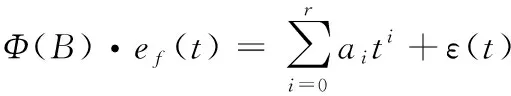
(33)
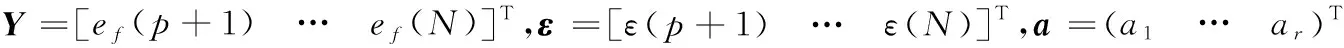

(34)

a=(XT·X)-1·XT·(Y-M·φ)
(35)
RSS=(Y-M·φ)T·(I-H)·(Y-M·φ)
(36)
式中:投影矩阵H=X·(XT·X)-1·XT,I为单位阵。由于式(36)是关于φ的二次函数,则φ可由下式求得:
φ=[MT·(I-H)·M]-1·MT·(I-H)·Y
(37)
由式(37)求得自回归系数φ后,将其代入式(36),即可得到零均值高斯白噪声ε(t)的方差估计值
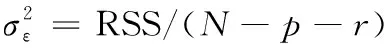
(38)
关于AR模型阶数和多项式阶数的确定,可以采用AIC准则,即:
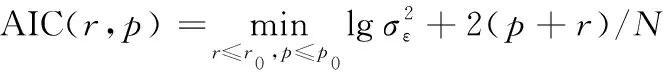
(39)
在实际应用中 ,一般取多项式阶数不超过3阶,自回归系数不超过30阶。
2 试验结果分析
为了保证定位结果的可靠性和准确性,一般要求信号中心频率恒定,接收信号的频率测量精度小于100 Hz,信号持续时间大于30 s。图6显示了测频定位误差与测频的关系,其中,信号接收时间为30 s,采样间隔为20 ms,辐射源频率为1 500 MHz,蒙特卡洛仿真次数为100次。
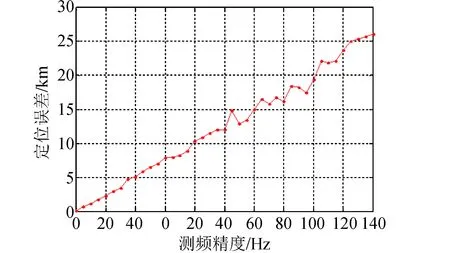
图6 测频定位误差与测频精度的关系Fig.6 Relation between positioning error and frequency measurement precision
在实际仿真试验中,计算结果为(东经122.948 7°,北纬30.918 8°)与(东经131.618 4°,北纬32.635 3°),根据测向结果的辅助人工判证,定位结果应为(东经122.948 7°,北纬30.918 8°)。在实际试验过程中,分别对多个固定通信辐射源进行了定位,定位精度较以往提高了10 km。此外,还对手持终端进行了定位测试试验,采用普通对讲机,信号为FM话音调制信号,试验结果表明,定位误差(CEP)也得到了大幅度提高。
3 结束语
本文提出了利用单颗卫星单个通道在不同位置上测量信号的多普勒频率实现对地面固定辐射源的无源定位方法,该方法具有有效载荷简单、对卫星姿态无特殊要求、定位收敛快、精度较高等优点。同时,探讨了多普勒频率测量误差预处理技术,以及基于PAR模型的系统误差分离技术。通过对测量误差的分离与处理,可以大幅度提高频率测量数据的精度,从而保证后续测频定位精度。最后,通过仿真试验和工程实际,验证了单星测频定位技术的有效性和准确性。
