基于显式力控制的空间机器人抓捕碰撞力控制方法

西北工业大学 航天学院,西安 710072

空间机器人抓捕目标过程中涉及两个空间物体之间的接触，对于自由飞行空间机器人来说，接触碰撞造成的影响主要有三个方面：一是在基座可控范围内，碰撞力越大，碰撞次数越多，维持系统稳定所消耗的推进燃料越多；二是当碰撞力超过基座控制范围，会造成机器人系统失稳；三是接触力增大到一定程度，会对抓捕机构造成损坏。因此接触碰撞阶段是整个抓捕过程中危险系数最高的阶段。接触碰撞与抓捕控制涉及抓捕机构的空间构型、接触表面的形状与材料特性，抓捕机构状态的计算、目标速度与位置的测量与目标的质量特性等诸多因素。真实的接触碰撞动力学模型是个高度非线性的复杂模型，其精确建模的难度极大，因此抓捕接触碰撞力控制是在轨抓捕技术中的难点和重点。

针对抓捕接触碰撞控制问题，Wee等[1]提出了一种梯度投影方法来进行笛卡尔空间的路径规划以使得接触时的冲击力最小化，但该方法要求机器人系统机构具有运动学冗余，并且该梯度算法容易陷入局部最优。Zheng等[2-3]给出了“冲击系数”和“冲击椭圆”碰撞冲击力特性，并在动量守恒的基础上，基于虚拟转子惯量的概念提出了扩展逆惯性张量(Ex-IIT)的概念，这样就可以在速度级上描述问题而无需测量碰撞力。Nenchev等[4-6]对如何利用“零反作用空间”进行了充分的讨论，采用耦合惯量矩阵的零空间解决了本体与机械臂之间的动力学耦合问题。作者同时指出，利用该方法获得的关节速度不会影响动量的分布。Shibli,M等[7-8]建立了空间机器人和目标卫星模型，设计了机器人抓捕目标的自适应逆动力学控制器。徐文福等[9]提出了一种将经典的选择矩阵进行加权处理的改进力/位控制方法，使力控制和位置控制的切换更加平滑。危清清等[10]将抓捕过程中的接触碰撞力简化为作用在抓捕机构上的脉冲力进行研究，但是实际中的接触力要复杂的多。MAO[11]利用仿真器对微重力环境下的接触动力学进行了研究。DIAO等[12]提出了减小碰撞力对空间机器人系统影响的算法。MAO等[13]又根据末端执行器的几何构型、抓捕机构的状态和观测得到的目标状态来预估接触力的方向，并基于此优化得到恰当的捕获时间和捕获位置，使得接触碰撞对系统的影响最小。魏承等[14-16]提出了一种空间机器人“动态抓捕域”的概念，并将其运用于捕获浮游目标的抓取控制 ，但他们是将浮游目标假设为质点，目标姿态可控，没有考虑到目标及抓捕机构的空间构造。陈钢等[17]针对空间机器人目标捕获过程中的碰撞问题，提出了一种碰撞运动分析算法，并且证明了该算法的正确性和适用性。刘厚得等[18]针对航天器抓捕后复合体系统失稳问题，提出了关节阻尼控制和关节函数参数化等两种协调稳定控制方法，实现了系统角动量的管理和重分配 。Yoshida等[19-23]研究了空间机器人系统之间的接触动力学，在捕获非合作目标过程中基于阻抗控制试验分析了机械臂与被动飞行器之间的碰撞过程 ，同时在如何减小冲击力上提出有效控制策略。Matsumoto 等[24]针对 Hyper-OSV 进行了抓捕策略研究，并对这些策略进行了分类讨论 。

以上对于抓捕接触碰撞控制研究的侧重点都是在研究接触碰撞的基础上寻求减小末端冲击的方法，鲜有对抓捕过程满足平稳性要求的碰撞力控制研究。为此本文提出基于任务优先级方法求解机器人系统运动逆解，采用显式力控制的接触碰撞力控制方法，通过与基于外力控制方法进行比较分析，验证所提方法对抓捕接触碰撞力控制的有效性，为解决空间机器人目标抓捕接触碰撞力控制问题提供技术支撑。

1 空间机器人运动学和动力学模型

1.1 运动学模型

如图 1所示，空间机器人由基座、4自由度操作臂以及操作手爪构成。将惯性系记作ΣI，体坐标系记作Σb，其中体坐标系原点位于基座质心，x轴为机械臂的安装方向，z轴根据推进器安装位置确定，y轴指向与另外两个轴构成右手直角坐标系。一般情况下为方便计算，使初始时刻体坐标系与惯性坐标系平行。本文运动学建模采用DH参数法，即将基座看做连杆0，然后从机械臂第一节连杆开始，依次递推，直到最后一节机械臂，依次记作1,2,3,…,n。在基座上，机械臂的安装位置坐标系记作Σ0，为了方便，一般让其与体坐标系平行；连杆i末端的坐标系记作Σi，其x轴与该连杆的方向相同，从该连杆的头部指向尾部，其z轴的方向为该连杆与上一节连杆之间的关节转轴方向，y轴指向与另外两个轴构成右手直角坐标系。连杆i+1绕Σi的z轴旋转过的角度记作θn+1。连杆坐标系之间的变换利用DH参数依次递推得到。本文将图 1中位于机械臂末端的坐标系Σ4另记作Σe。

图1 空间机器人DH坐标Fig.1 DH coordinate diagram of space robot

定义惯性系下体坐标系的位置和姿态为：

(1)

定义体坐标系下体坐标系相对于惯性系的线速度和角速度为：

(2)

则：

(3)

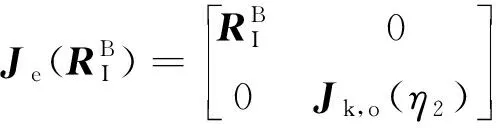
定义体坐标系下空间机器人系统速度为：

(4)

可以将式(4)连同关节角写成更加紧凑的形式：

(5)

定义惯性系下末端坐标系的位置和姿态为：

(6)

末端位姿ηee可表示为体坐标系位姿η和机械臂关节角q的函数，即：

ηee=k(η,q)

(7)

定义体坐标系下末端坐标系线速度和角速度为：

(8)

惯性系下机械臂末端的位置可以表示为：

(9)

对式(9)求导可以得到：

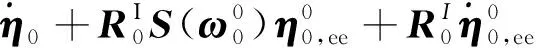
(10)

(11)

定义：

(12)

将式(11)和式(12)代入式(10)可以得到：

(13)

同时，有：

(14)

(15)

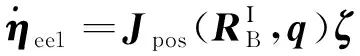
(16)

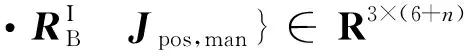
(17)

惯性系下机械臂末端的角速度可以表示为：

(18)

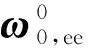
利用固定基座末端的雅克比矩阵可以将式(18)写为：

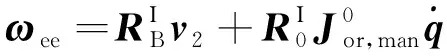
(19)

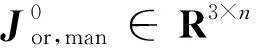
(20)

则式(19)最终可以写为：

(21)

式中：

(22)

最终得到表示机械臂末端六自由度完整运动学方程：

(23)

(24)

1.2 动力学建模

本文采用牛顿-欧拉迭代法建立空间机器人动力学模型。安装在基座上机械臂上的任意连杆i的惯性力和惯性力矩可以表示为：

(25)

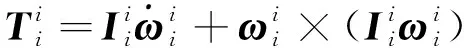
(26)

(27)

(28)

根据式(25)～式(28)可以进行相应的外向和内向迭代计算。

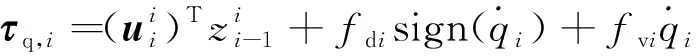
(29)

式中：fdi和fvi是关节的干摩擦系数和粘性摩擦系数。

定义：

τq=[τq,1…τq,n]T

(30)

τ=[τvτq]T

(31)

式中：τv为空间机器人系统受到的合外力或力矩；τq为关节控制力矩。

空间机器人系统的动力学方程最终可以表示为：

(32)

2 基于显式力控制的碰撞力控制方法

图 2所示为本文所涉及的操作手及目标结构。其中，O为末端D-H坐标系的原点，x、y、z分别为末端D-H坐标轴,操作手安装在机械臂末端，e1,e2,e3分别为3个指与手掌的铰链连接点，抓捕过程中手指e1a1b1,e2a2b2,e3a3b3分别绕e1,e2,e3同时转动实现手爪的开合，完成目标抓捕；平面c为手眼相机前端平面，该平面与手掌平面(即e1,e2,e3组成的平面)平行。为简化模型，假设抓捕目标为单独圆柱杆，d1d2为圆柱杆中心线，半径为r1。手指横截面为椭圆，对应的短轴半径为r2。

显式力控制方法是一种力位混合控制方法[26]，它将运动控制和力控制分开，是一种直接力控制方法，相比与通过控制机器人系统位置实现力控制目标的外力控制方法(间接力控制方法)，其控制思想简单，容易理解。基于显式力控制的碰撞力系统控制框图如图3所示。

图2 手爪示意Fig.2 Schematic diagram of the claw

图3 基于显式力控制的碰撞力控制系统框图Fig.3 Block diagram of collision force control system based on explicit force control

2.1 碰撞模型

本文采用赫兹接触力碰撞模型计算作用在目标上的接触力Fcmi，

(33)

式中：kg为接触碰撞刚性系数；kc为接触碰撞阻尼系数；δ为形变量，目标与手指碰撞的产生的形变量δi=di-(r1+r2),i=1,2,…,6，与相机平面碰撞产生的形变量δ7=d7-r1；ni为作用在目标上的碰撞接触力方向。在末端D-H坐标下，根据设定的手爪闭合速度，计算当前手指位置，并分别计算目标轴线到手指e1a1b1(包括线段e1a1，线段a1b1)，e1a1b1(包括线段e2a2，线段a2b2)，e3a3b3(包括线段e3a3，线段a3b3)和c平面的距离d1,d2,d3,d4,d5,d6和d7。

作用在目标上的碰撞接触力合力为Fcm，

Fcm=∑Fcmi,i=1,2,…,7

(34)

作用在抓捕机构上的合力Fcs=-Fcm。需要说明的是此处Fcmi,Fcm,Fcs均为在最后一个机械臂的坐标系下。

2.2 任务优先闭环运动学控制

本文空间机器人系统共10个自由度，大于末端位姿的6个自由度，因此是运动学冗余的。

任务优先冗余解决方法[28-29]可以很好地实现优先级高的任务，同时兼顾次优的任务。本文将基于任务优先方法的运动学闭环控制方法与接触碰撞力控制融合，可获得较好的接触力控制效果。

对于任意任务a：

σa=σa(η,q)

(35)

相应的雅可比矩阵是：

(36)

定义代价函数：

f=ζTζ

(37)

满足式(23)的约束，通过使得代价函数f最小，可以得到：

(38)

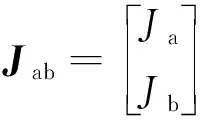
(39)

3个任务的方程为：

(40)

当利用上述算法积分求解基时，会造成数字漂移，使得实际得到的值与期望值有偏差。对此可以通过加入比例项尽量消除这些积分漂移，由此可得式(40)的闭环形式为:

(41)

式中：ka,kb,kc是选取的反馈系数，可以使相应的积分漂移收敛到零。特别地，选取控制机械臂末端执行器位姿闭环形式为：

(42)

得到闭环形式的ζr后，便可以利用逆运动学得到惯性系下的参考轨迹：

(43)

2.3 反馈线性化动力学控制方法

空间机器人整个系统是一个典型的多体系统。本节利用反馈线性化、参数线性化的相关理论，设计相应的控制器，控制基座推力、力矩以及关节力来跟踪基于任务优先方法的运动学闭环控制方法(第2.2小节)给出的参考轨迹。

整个多体系统的动力学方程为：

(44)

令控制律为：

(45)

式中：

(46)

而

(47)

(48)

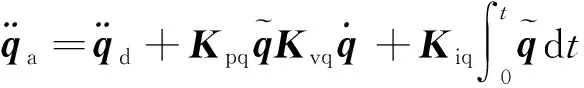
(49)

2.4 接触碰撞力控制律设计

由图3及上述推导可得基于显式力控制的接触碰撞力控制方法的控制律：

τ=τM+τF

(50)

式中：τ为施加的运动控制力矩；τF为施加的力控制力矩，

(51)

(52)

基于外力控制的接触碰撞力控制律为：

(53)

其中

(54)

3 接触碰撞力控制仿真分析

本节将对基于显式力控制的抓捕接触碰撞力控制方法和基于外力控制的抓捕接触碰撞力控制方法进行仿真对比分析，其中A组为后者的仿真结果，B组为前者的仿真结果。仿真条件如下：

1)初始时刻目标在末端坐标系中的坐标为[0.07,0.01,0]；

2)手爪闭合旋转速度为w=0.154 6 rad/s。

仿真结果如图4～图10所示。

图4 两组基座控制力仿真结果Fig.4 Simulation results of two groups of base control force

图5 两组基座控制力矩仿真结果Fig.5 Simulation results of control moment of two groups of bases

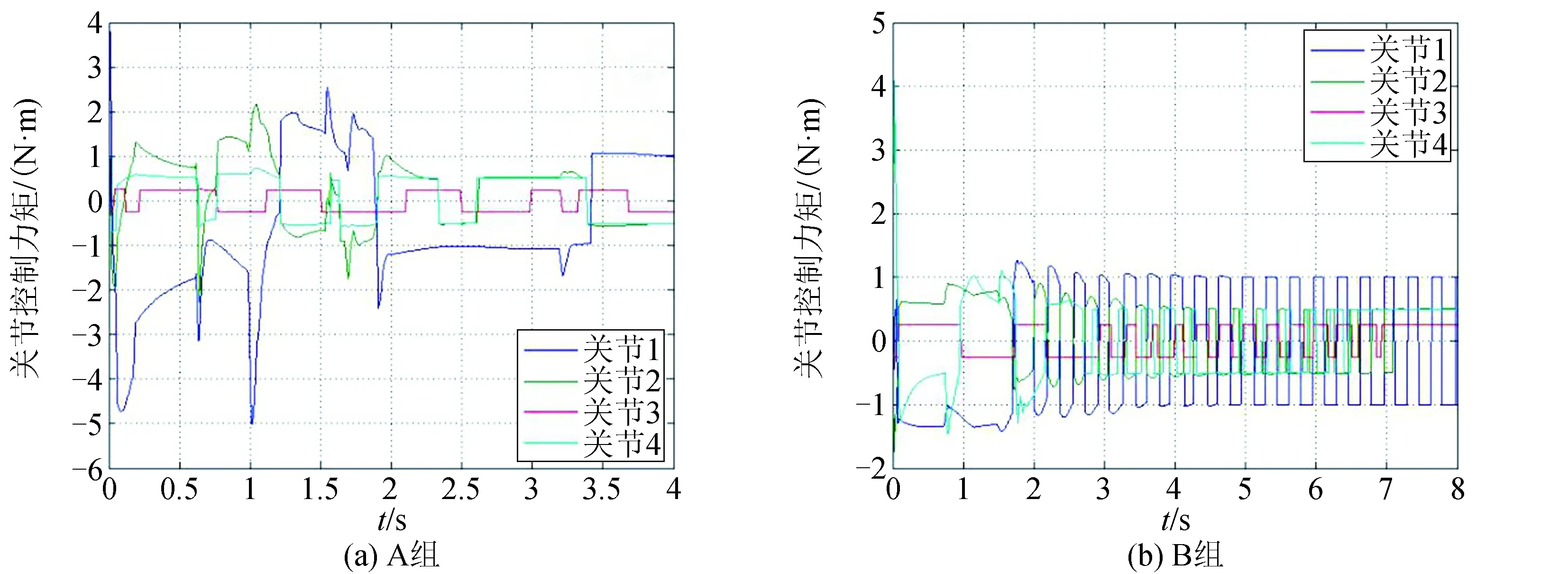
图6 两组关节控制力矩仿真结果Fig.6 Simulation results of two groups of joint control moments

由图4～图6的仿真结果可以看出，A组的基座控制力和力矩约为B组基座控制力和力矩的10倍，并且A组基座力和力矩变化曲线有多处突变，B组基座力和力矩变化曲线相对平缓。对于关节控制力矩来说，B组关节力矩在初始时刻较大，之后保持在较小的范围内，且变化较为规律，A组整体来讲关节力矩较大且变化没有规律。

从图7可以看出，A组控制下基座的位姿扰动量约为B组控制下机器人系统位姿扰动扰动量的2倍。

由图8～图10可见，A、B两组碰撞接触力的变化趋势以及各个接触力的最大值相同，碰撞合力的最大值相近，基于显式力控制的过程呈现出振荡收敛的特性，而基于外力控制下的曲线变化相对比较平滑。两组目标质心轨迹趋势大致相同，B组过程中存在小幅震荡。

图7 两组空间机器人系统位置仿真结果Fig.7 Simulation results of two groups of space robot systems

图8 两组接触碰撞合力仿真结果Fig.8 Simulation results of two groups of contact collision resultant force

图9 两组接触碰撞力仿真结果Fig.9 Simulation results of two groups of contact collision forces

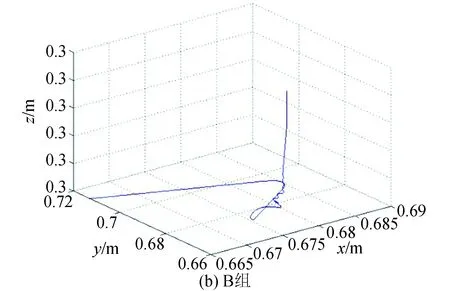
图10 两组目标质心运动轨迹仿真结果Fig.10 Simulation results of the motion trajectories of the two groups of target centroids

4 结束语

本文针对空间机器人抓捕漂浮目标过程中的接触碰撞力控制问题，提出了一种基于显式力控制的空间机器人抓捕碰撞力控制方法。研究结果显示：

1)基于显式力控制的抓捕接触碰撞力控制方法可以有效的控制接触碰撞力，在抓捕过程中使系统处于平稳状态。

2)基于显式力控制的抓捕接触碰撞力控制方法所需的基座控制力和力矩远小于基于外力控制的抓捕接触碰撞力控制方法所需的控制力和力矩，满足空间机器人系统的稳定和尽可能少的能量消耗要求。

分析碰撞力对目标的影响时，忽略了目标的旋转运动，因此针对旋转运动较大的目标还需要进一步考虑目标旋转运动的影响；此外，基于接触表面的摩擦和阻滞较小的前提，所采用的碰撞模型没有考虑接触表面的摩擦和阻滞系数，这一点在其不可忽视的情况下也需要进一步研究。