计算VaR的三种历史模拟法的实证对比研究

(天津财经大学 天津 300222)

一、理论基础

(一)在险价值VaR

给定置信水平1-α和时间间隔t，如果一间实体机构在时间间隔t内预计损失额超过M的概率小于α，则称这家实体机构在时间间隔t内的VaR为M，即P{损失额>M}=α。

(二)一般历史模拟法

一般历史模拟法将历史值作为未来可能的实现值，将历史的损益分布作为未来的损益情况，进而通过历史数据得到表示未来一段时间一定置信水平下的VaR。其计算步骤为首先确定置信水平1-α和时间间隔t；然后计算历史区间内每天的收益率；最后对得到的收益率进行有放回的抽样，将得到的损失情况由小到大排序，根据置信度选择相应的分位点，即为所求的VaR值。

(三)加权历史模拟法

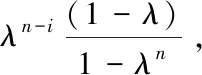
(四)过滤历史模拟法

对一般历史模拟法中的波动率进行更新就形成了过滤历史模拟法。过滤历史模拟法的步骤为，首先对历史收益率建立GARCH模型，取其残差et-1,et-2,……,et-k,…，并对其残差进行标准化；然后对标准化的残差进行随机抽样得到对应的VaR值，显著性水平为α的VaR对应的收益率为q(α)=μt+σtG-1(α)。

二、实证分析

(一)数据说明与数据分析

由于上证综合指数反应我国股票市场的走势，本文选取上证综合指数1999年12月31日—2019年6月10日的共4707个收盘价数据，计算其对数收益率，用前3706个收益率数据来计算不同置信水平下区间为1天的VaR值，用剩下的数据来进行回顾测试。

我们做出历史区间内对数收益率的折线图，如图1所示。发现对数收益率围绕0的上下波动，可以看作是平稳的时间序列。

图1 对数收益率的时序图

对收益率数据进行ARCH效应的检验。分别对收益率数据和收益率平方数据进行Box-Ljung检验，得到的P值分别为0.1266、2.2e-16，收益率数据不存在序列相关，收益率平方数据存在序列相关，所以序列存在ARCH效应，可以建立GARCH模型。

(二)三种历史模拟法的实证分析

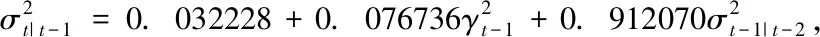
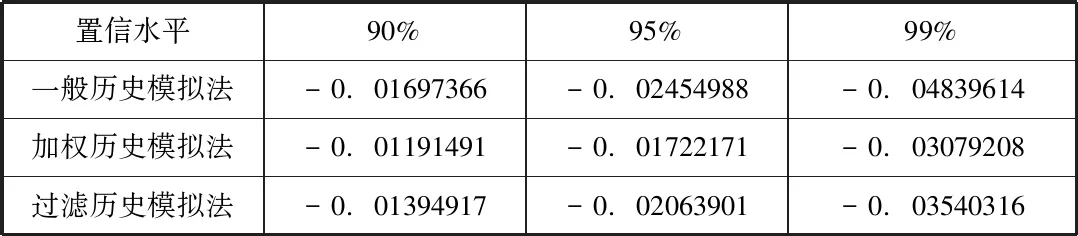
表1 三种历史模拟法的VaR值

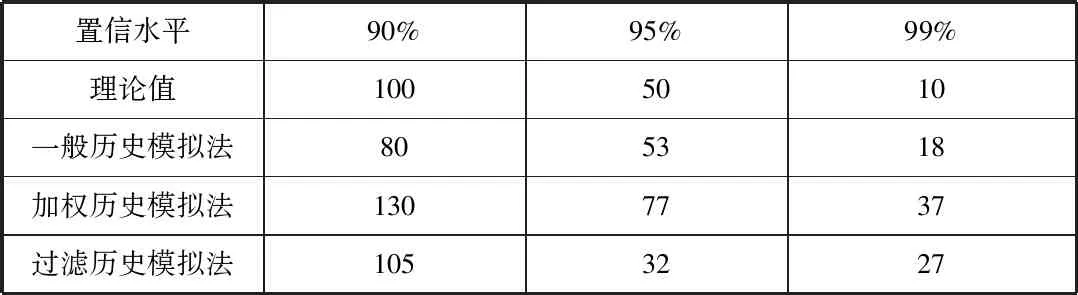
表2 三种历史模拟法不同置信水平下的失败次数

通过比较分析，我们可以看出：

①就整体结果而言，一般历史模拟法的误差最小。

②加权历史模拟法在三种历史模拟法中的表现最差。

③在95%置信水平下过滤历史模拟法的超限次数小于理论值，而一般历史模拟法和加权历史模拟法均超过理论值，但一般历史模拟法与理论值相差最小。

三、研究结论

根据以上结果我们得出如下结论：在样本区间内，95%置信水平下，过滤历史模拟法对损失情况有较为明显的高估，而一般历史模拟法的结果与实际相近，如果是厌恶风险的投资者可以选择过滤历史模拟法来预测损失；90%置信水平下，一般历史模拟法对损失情况有高估现象，而过滤历史模拟法的结果与实际相近，如果不是厌恶风险的投资者可以选择过滤历史模拟法来预测损失；在高置信水平下，三种历史模拟法的表现均较差，不适合用历史模拟法来计算VaR值。