船舶轴频电场跟踪*

孙宝全，颜 冰，张伽伟，姜润翔

(海军工程大学 兵器工程学院， 湖北 武汉 430033)

船舶轴频电场与船舶静态电场一样是船舶重要的水下电场信号，相比于船舶静态电场，轴频电场频率低、传播距离远，具有明显的线谱特征[1-2]。轴频电场信号的包络可视为准静态电场信号，可以由水平电偶极子反演得到[3]，其中包含有位置信息，可以用来实现对船舶目标的跟踪定位。目前轴频电场多用于目标的被动探测[4-6]，而在跟踪定位领域的应用鲜见报道。在声学环境复杂的区域，相比于声学跟踪定位方法，电场跟踪所受影响相对较小，可以作为声跟踪定位的一个有效补充。以卡尔曼滤波为代表的滤波估值算法可以根据传感器量测信息对目标的相关参数进行实时的估计，在目标跟踪领域获得越来越广泛的研究和应用[7]。利用船舶轴频电场对船舶进行跟踪主要应用在水雷、水下预警防护系统中，由于此类装备对功耗和计算资源有较高的要求，为此对滤波算法的复杂度也提出了较高的要求。相比于粒子滤波，卡尔曼滤波计算方法简单，计算量小，更利于在水下武器中的工程化实现。

船舶轴频电场的包络可视为准静态信号，因此可以将其视为静态电场(Static Electric field，SE)信号对其进行建模和跟踪。但是与静态电场不同的是，轴频电场包络获得的是电场模值，因此也丢失了一部分的方位信息。

文献[8]中提出了一种在大初始误差条件下保持滤波稳定性的渐进更新扩展卡尔曼滤波(Progressive Update Extended Kalman Filter，PUEKF)。算法相比传统卡尔曼滤波算法具有更好的稳定性和收敛性。本文将以PUEKF为基础，对轴频电场包络的跟踪进行研究，探索轴频电场在船舶跟踪的可行性以及相关问题的解决方案。

1 船舶轴频电场包络跟踪问题描述

跟踪问题状态空间模型为[9]：

(1)

其中：xk∈Rn为k时刻的n维状态向量；yk∈Rm为k时刻m维观测向量；状态转移函数a:Rn→Rn；观测函数h:Rn→Rm；wk-1∈Rn为状态噪声向量，vk∈Rm为观测噪声向量，且wk-1～N(0,Qk-1)，vk～N(0,Rk)，Qk-1为过程噪声协方差矩阵，Rk为观测噪声协方差矩阵，{wk-1}和{vk}不相关。

1.1 观测方程

在一定距离条件下，船舶轴频电场包络可以用一个水平偶极子进行模拟：

1)利用希尔伯特变换计算轴频电场信号的峰值包络，并对峰值包络进行0.5 Hz的低通滤波，得到轴频电场信号包络；

2)采用水平电偶极子对轴频电场包络信号建模；在如图1所示的“空气-海水-海床”三层均匀介质条件下，任意场点Pf处的电位信号为[10]：

Φ(x,y,z)=Φx(x,y,z)+Φy(x,y,z)

(2)

其中：x,y,z是场点坐标；x0,y0,z0是场源位置坐标；η=(σ1-σ2)/(σ1+σ2)是海底反射系数；σ1是海水电导率；σ2是海床电导率；D为海水深度；h为坐标系原点深度。r1k,r2k,r1m,r2m分别为：

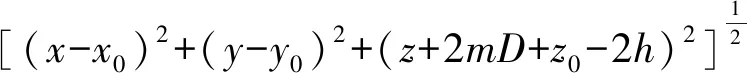
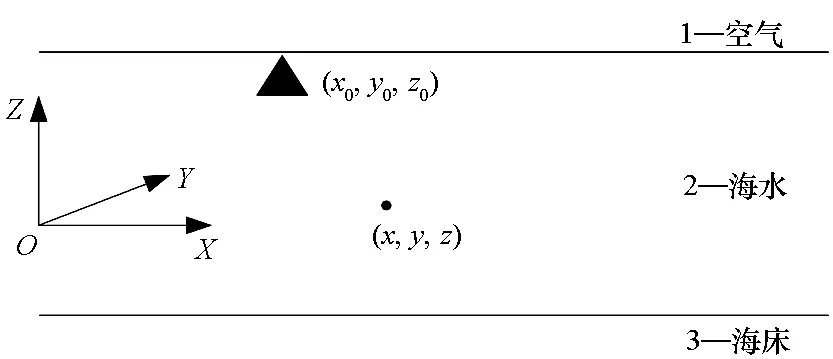
图1 空气-海水-海床三层均匀介质坐标系Fig.1 Air-seawater-seabed three-layer uniform media coordinate system

那么便可以得到相应的电场信号：

E=(Ex,Ey,Ez)=-Φ

(3)

其中，Ex,Ey,Ez分别为：

则在第j(j=1,2,…,J)个电场传感器量测到的目标包络信号可建模如下：

(4)

(5)

1.2 状态方程

根据观测方程定义k时刻船舶目标状态向量：

(6)

其中，rk=[x,y,z]T，Vk=[Vx,Vy]T(忽略z方向上运动)。

根据船舶目标低机动假设，将船舶目标运动建模为离散白噪声加速度(Discrete White Noise Acceleration, DWNA)模型，因此式(1)中a(·)为线性变换F，即：

Ts为采样时间间隔。

2 基于最大似然选择的多初值PUEKF

船舶轴频电场包络跟踪中，单凭包络信息无法确定船舶的起始状态，而滤波初值的设定对于滤波算法的性能具有至关重要的影响。现有的滤波算法中不论是分布近似方法(粒子滤波类)还是矩近似方法(卡尔曼滤波类)，均不能保证任意初值条件下的滤波收敛性，根本原因在于参与滤波更新的量是根据当前一步预测状态，因此初值与真实值之间相差过大会导致滤波发散。其实对于水面目标跟踪，滤波初值主要确定的是水面初始距离rxy,0，航行角ψ0，速度V0，电偶极矩p0，那么便可得到滤波初值为：

x0|0=[rxy,0cos(ψ0);rxy,0sin(ψ0);z0;

V0cos(ψ0);V0sin(ψ0);p0]

对于水面目标而言，z0可由传感器深度得出。V0可由跟踪的目标特性由经验值进行设定。最难确定的是rxy,0，ψ0，p0。由电场的观测模型可知，在传感器位置已知的情况下，|E|是r和p的函数，因此可以根据|E|设计一个r和p的初值估计方法，然后依据多初值模型基本原理[11-12]，假定多个初值起始滤波，并由最大似然法选出最优结果。

2.1 基于最大似然选择的多初值模型

假定目标真值(或者滤波最优初值)是多个可能假设初值中的一个，且概率相等，则

(7)

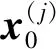
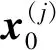
(8)

那么

(9)

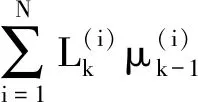
(10)

其中

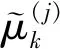
(11)

2.2 多初值模型参数确定

三层介质下点电源电场公式较为复杂，根据其推算出初始目标距离等同于滤波算法本身，为此设计一个简化公式估计距离。

在全空间充满电导率为σ的导体媒质，那么场点处的标量电位为：

(12)

那么对应的电场模值为：

(13)

由恒稳电场的镜像理论，在空气-海水-海底三层介质中，位于海水中的源在海水中产生的静态电场等效为无限大海水区域中，源及其通过两个界面形成的无数个镜像在场点处产生的电场叠加。镜像的强度与源强度相同，只是与场点的距离发生了变化。为此3层介质中电场模值的计算可以在源强度中加一个修正系数mx，mx可取一个经验值，与海水深度有关，则

(14)

那么由此便可以根据电场强度模值估算距离

(15)

对于目标源强度，可以根据经验设置几个可能值p(i)(i=1,2,…,K)，其中p(1)与p(K)分别对应可能的最小和最大源强度。则在p(i)(i≠1,i≠K)应在p(1)与p(K)的数值范围之间等比例分布或者根据经验设定，等比例分布可按式(16)进行，则

此外，本研究发现拒绝作业治疗组主要照顾者的焦虑情绪得分随着时间有下降，但是抑郁情绪得分随着时间却逐渐增高，且每个时间点的两两比较均有显著统计学意义。临床中抑郁的症状常有内疚、自责、绝望感等，且抑郁的病人常采用负面的应对方式。国外有学者对120名烧伤患儿家属调查发现，家属对小儿意外烧伤的反应及其应对方式对患儿的心理康复起着重要的作用[11]。Simons等[12]采用案例的方法认为，家属的无效应对方式有可能给烧伤后的治疗带来风险。这提示主要照顾者的抑郁情绪更需要引起临床工作者的重视。

(16)

2.3 渐进更新扩展卡尔曼滤波

(17)

那么结合EKF的基本步骤可得PUEKF算法步骤，如算法1所示。

算法1 PUEKF算法步骤

综上所述，可给出多初值渐进更新扩展卡尔曼滤波(Multiple Initial PUEKF，MI-PUEKF)跟踪算法的基本步骤为:

4)进入下一时刻的滤波或到达预定时刻后终止滤波。

3 传感器阵列

基于最大似然法的MI-PUEKF可以解决如何选取初值，并提供了一种如何判断正确轨迹的方法。但是这种可行性必须有一个前提，那就是观测模型可观，即其解具有唯一性。轴频电场包络丢失了方向信息，从观测方程以及电场的特性可知，对于单个传感器，同一个信号值可以对应几个状态，此时，滤波器的结果是不可信的。为此在对轴频电场包络的研究中必须研究传感器阵列所需最少传感器数目及其排布方式。

考虑如下的仿真情景，目标电偶极矩p=100 A·m；以传感器阵列为基础建立右手坐标系，传感器所在线为Y轴，传感器中心点为坐标原点，X轴过原点垂直于Y轴；Z轴向上。假设目标分别从π/4，3π/4，5π/4，7π/4四个方向匀速通过传感器阵列，观察传感器接收到的信号特征。

不失一般性，假设三个三轴电场传感器，其位置分别为[0,5,0;0,0,0;5,0,0]，船舶的其他初始参数见表1。

表1 仿真场景参数

图2所示是三个传感器上的|Ex|信号。从图2(a)可以看出传感器1(0,5,0)上航向π/4，3π/4的两个轨迹的|Ex|是相同的；5π/4，7π/4两个轨迹的|Ex|是相同的。|Ey|,|Ez|亦是如

(a) sensor#1 |Ex|

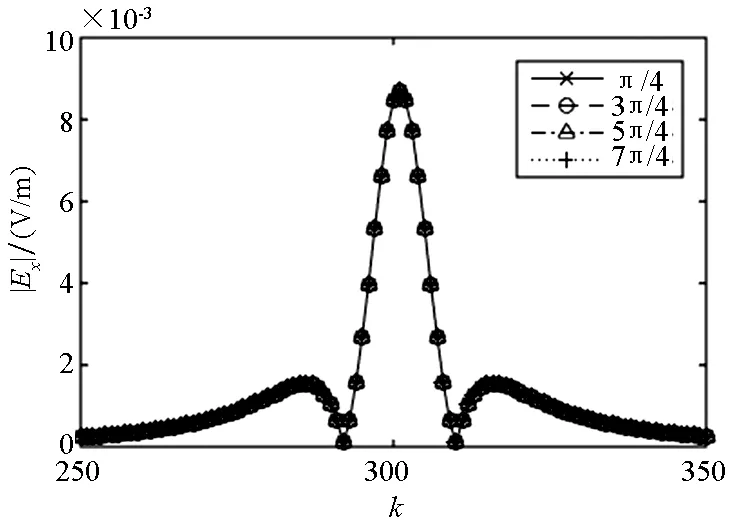
(b) sensor#2|Ex|

(c) sensor#3|Ex|图2 传感器上|Ex|信号Fig.2 Signal |Ex| on sensor

此。从图2(b)～(c)可知，传感器2、传感器3上的信号也有类似特征，整理总结如表2所示。其中数字相同表示按信号相同分组。

表2 传感器上信号特征分组

由此可以总结一个基本结论，对于原点上的传感器，基于X轴和Y轴对称的轨迹产生的信号是相同的。对于位于X(Y)轴上的传感器，基于X(Y)轴对称的轨迹产生的信号是相同的。因此，在滤波跟踪中至少需要3个传感器，且3个传感器不能位于同一直线上才能保证解的唯一性。

4 仿真结果及分析

考虑如下的仿真情景，电偶极子电偶极矩p=100 A·m；以传感器阵列为基础建立右手坐标系，传感器所在线为Y轴，传感器中心点为坐标原点，X轴过原点垂直于Y轴；Z轴向上。选用三个三轴电场传感器，其位置为o1,2,3，其他初始状态见表3；此外，过程加速度噪声强度σx=σy=0.1，α=0.001；观测噪声协方差矩阵Rk=σ2I2×2，σ=1×10-7。

表3 仿真场景参数

对MI-PUEKF滤波器配置，假设目标源强度分布在K=3等级上，即p1=50 A·m，p1=100 A·m，p1=200 A·m。利用式(15)得到三个可能的目标平面初始距离。在各个距离上假定四个起始方位π/4，3π/4，5π/4，7π/4，总的滤波器数量为K·NF=12。

(18)

仿真次数MC=100。

(a) SensorPosition1

(b) SensorPosition2图3 各个初值条件下滤波器的总均方根误差Fig.3 Total root mean square errors of the filter under each initial value condition

(a) SensorPosition1

(b) SensorPosition2图4 各个初值条件下滤波器的均方根误差曲线Fig.4 Root mean square error curves of the filter under each initial value condition

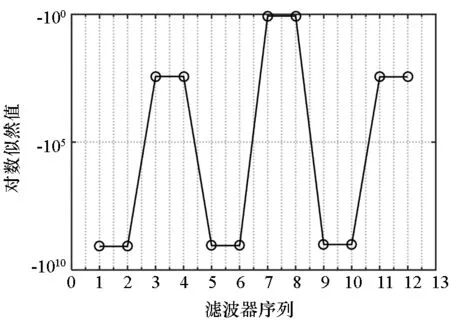
(a) SensorPosition1

(b) SensorPosition2图5 各个初值条件下滤波器的对数似然值Fig.5 Logarithmic likelihood value of the filter under each initial value condition

(a) SensorPosition1

(b) SensorPosition2图6 跟踪结果(对数似然值最大的前3个模型)Fig.6 Tracking results (models of the first three maximum logarithmic likelihood value)

仿真结果表明：

1)轴频电场包络跟踪所需传感器数目至少三个，且不能位于一条直线上；

2)在传感器阵列满足要求的情况下，基于最大似然的多初值模型可以解决轴频电场包络跟踪先验信息缺失的问题，且基于对数似然函数值可以选择出滤波最优的结果；

3)三个收敛的初值模型其初始假设方位为3π/4，相比其他假设，与真实方位最接近，可见，相比于距离而言，跟踪误差对方位先验信息更加敏感。

5 结论

本文研究了利用船舶轴频电场包络对船舶进行跟踪的可行性。船舶轴频电场包络可以视为准静态电场，但是仅可以获得电场模值信息，因此丢失了一部分方位信息，这对传感器阵列提出了要求，传感器数目不能少于三个，至少有三个传感器不在一条直线上。针对轴频电场包络跟踪中先验信息缺失的问题，文章引入了一种基于最大似然选择的多初值渐进更新扩展卡尔曼滤波方法。仿真结果表明，轴频电场包络跟踪中滤波方法对方位先验信息更加敏感，多初值渐进更新扩展卡尔曼滤波方法能够有效地解决先验信息缺失条件下的轴频电场包络跟踪问题，具有重要的实际意义。