交互式Pareto前沿可视化决策*

胡佳鑫，杨乐平

(国防科技大学 空天科学学院， 湖南 长沙 410073)

在高维多目标优化问题中，目标向量构成了多目标优化问题的非劣最优目标域，称为Pareto前沿。一般地，各子目标之间存在复杂的冲突性，决策者需要深度发掘Pareto前沿特性并结合实际需求作出最终选择。高维多目标可视化技术将Pareto前沿投影至低维观测空间，提供用户直观有效的决策辅助，广泛应用于数据挖掘、决策分析、任务规划以及多学科优化设计等领域，成为高维多目标优化问题的研究热点之一[1]。

为辅助决策者正确分析多维目标信息，多目标可视化技术应满足直观、有效以及简单等特点。目前，高维多目标可视化问题的研究成果主要分两类：

一类是完好无损地表现目标各维度信息，保证信息的不缺失。平行坐标系[2]与热图[3]是目前广泛应用的多目标可视化方法，其特点是将所有目标信息通过单一的视图呈现，虽然效果直观，但高维度空间势必会引起视觉混乱。散点图[4-5]通过将目标的各维度信息两两组合成图表进行对比分析，图表的数量随维度增长呈指数级增加，对于决策者在实际应用中十分不便。n维图表[6]是基于决策偏好的Pareto前沿可视化方法，该方法提出一种目标全局信息的共享机制，采用多图表分别绘制权重分配下各维度信息与全局信息的对比结果，能够有效地反映目标信息与决策偏好。但是，该方法的权重分配对于同时多个目标偏好的分层效果不佳。

另一类是对原始数据进行压缩降维，然后投影至低维观测空间进行可视化分析，如主成分图(Principal Component Biplots， PCB)[7]、星图[8]、基于分形的降维方法以及旋转其可视化方法[9]等。PCB是目前国外对于高维数据可视化非常有效的方法，该方法通过对原始数据矩阵进行奇异值分解，提取高维数据聚类特征后降维映射至低维观测空间完成可视化，具有较高的数据压缩质量。但是，该方法得到静态的轴向量与投影点，不能满足实际应用场景中决策者根据偏好调整参数的交互需求。

文献[11]提出了一种增强高维数据可视化效果的自适应径向轴图方法，根据交互更新的轴向量矩阵建立降维映射模型，对模型求解获得低维投影点，可视化效果直观有效。鉴于此思想，本文利用径向轴图的交互优势，提出一种基于径向轴图的交互式Pareto前沿可视化决策方法。首先，介绍了径向轴图的基本原理，径向轴图较好地降低了数据降维映射带来的信息损失。然后，阐述了如何基于径向轴图实现Pareto前沿可视化决策，根据用户交互即时更新视图，辅助决策者正确把握目标性能趋势。最后，通过仿真实验以及与传统可视化技术的对比，证明了本文方法能够将决策偏好信息与Pareto前沿分布有效地结合显示，辅助决策者正确把握目标性能趋势，筛选出满足实际需求的可行方案。

1 Pareto前沿可视化问题

设Xf为多目标优化问题的可行解集，F(x)=(f1(x),f2(x),…,fm(x))为目标向量，所有Pareto非支配解的集合构成该多目标优化问题的Pareto非支配解集P*，如式(1)所示[1]。

P*={x∈Xf|∃x′∈Xf:x′≻x}

(1)

其中，x′≻x表示x′Pareto支配x，简称支配。

P*的目标向量构成了多目标优化问题的非劣最优目标域，即Pareto最优前沿，如式(2)所示。

PF={f1(x),f2(x),…,fm(x)|x∈P*}

(2)

Pareto前沿可视化问题主要解决将m维Pareto最优前沿PF降维投影至观测空间。本文仅考虑Pareto前沿在二维平面上的投影问题。

2 径向轴图原理

径向轴图方法通过将高维数据空间向低维观测空间投影变换来提供可视化决策功能。为方便讨论，本文考虑n维数据样本投影至m维观测空间，n≥3≥m，m=2。数据样本点表示为xd∈Rn，N个xd组成N×n数据样本矩阵Xd。每一个数据样本对应一个投影点p∈Rm，N×m投影点矩阵P。Xd由p与n个m维轴向量vi∈Rm,i=1,…,n表示，n个Vi组成n×m径向轴矩阵V。

对于降维投影方式的高维数据可视化问题，重点在于解决如何减小数据降维映射带来的信息损失。高维数据可视化的降维映射问题可描述为：

(3)

其中，F表示Frobenius范数，本文考虑通过欧几里得距离评估数据降维的损失。F-范数是由所有奇异值组成的向量2-范数，数值等于全部元素平方和的平方根。由于N×n数据矩阵各行数据样本xd是相互独立的，因此问题可转化为：

(4)

对于上式，径向轴图方法首先考虑提供决策者旋转、缩放径向轴功能，即轴向量的方向和模是任意的。该问题就转换成如何根据特定的轴向量矩阵V求解投影点p，使得pVT到xd的欧式距离比到子空间span{x1,x2,…,xn}中其他向量的欧式距离都短，即高维最小二乘问题。

一般情况下，n×m轴向量矩阵V是列满秩的，采用Moore-Penrose广义逆矩阵方法求解该问题，其解的形式如式(5)所示。

p=V†xd=(VTV)-1VT

(5)

由上式可知，V†可视为V的线性变换，投影点的求解过程可以在线性时间内完成，满足了交互式决策的实时性要求。

3 交互式Pareto前沿可视化决策方法实现

基于径向轴图的交互式n维Pareto前沿可视化实现需要考虑响应用户交互以及视图刷新问题。现阶段主流编程平台均能满足要求，例如C++、Java、C#等。由于篇幅有限，本文不赘述详细实现代码，主要给出交互式n维Pareto前沿可视化方法的具体实现步骤，方法流程如图1所示。

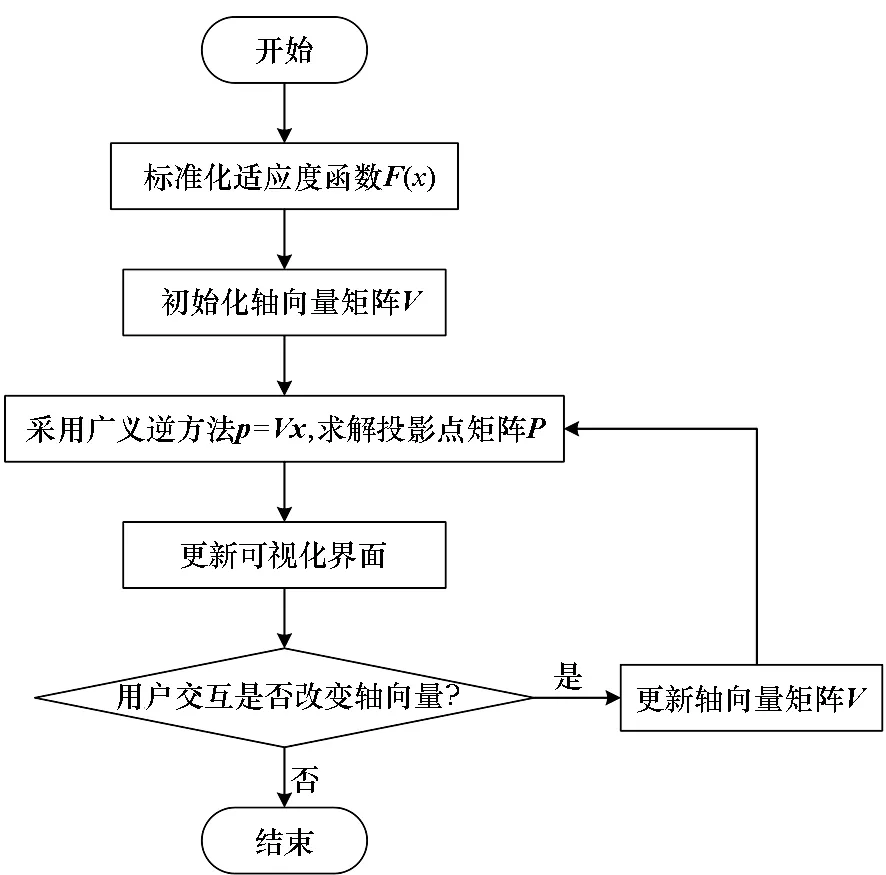
图1 方法流程图Fig.1 Method flow diagram

1)针对Pareto非支配解集P*中可行解各目标之间可能存在较大的数值差距，首先需要对各目标向量fi(x)(i∈{1,…,r})进行归一化处理，得到ki(x)，如式(6)所示。

(6)

2)初始化轴向量矩阵V，均匀分布各轴向量初始朝向，初始长度统一设为单位长度，如式(7)所示。

(7)

3)设由ki(x)=(k1(x),k2(x),…,kn(x))，i=1,2,…,N组成了数据矩阵Xk。获得数据矩阵Xk与轴向量矩阵V后，根据径向轴图原理，采用广义逆矩阵方法求解投影点p，即二维平面投影点坐标。

4)基于通用软件编程平台，根据投影点坐标绘制n维Pareto前沿信息。

5)根据决策者对可视化视图中各轴向量的交互操作，即对特定轴向量进行旋转、缩放，从而获得新的轴向量矩阵V。返回步骤3重新计算投影点矩阵。

基于径向轴图的交互式n维Pareto前沿可视化效果如图2所示。

图2 基于径向轴图的交互式Pareto前沿可视化效果Fig.2 Interactive visualization of pareto front based on radial axes plots

图2表示规模为50的Pareto前沿分布。其中，P点在各轴上的分量表示ki(x)子目标估计值。该目标域降维后的总离差等于1.17，估计值较为准确，满足决策分析可行性要求。通过旋转、拉伸或者缩短任一轴向量，视图动态更新投影点分布，直观反映决策偏好。同时，该方法支持决策者点击查看关注目标的各维度信息，准确把握各目标性能趋势，辅助决策者筛选出符合实际需求的最终方案。

4 仿真实验与结果分析

为验证基于径向轴图的交互式高维Pareto前沿可视化方法能够满足实际问题中的多目标决策需求。本文采用DTLZ1函数进行实验，并与目前主流应用的平行坐标系、散点图以及基于偏好的n维图表可视化技术进行对比分析，进一步验证本文方法的有效性以及优越性。DTLZ1函数为国际通用的无约束多目标优化标准测试函数。最小化目标函数如下：

式中，n=9,xi∈[0,1]。假设通过优化算法得到了Pareto非支配解集，种群为300。现采用主流的可视化方法对Pareto前沿进行绘制。其中，平行坐标系显示结果如图3所示，散点图显示结果如图4所示，考虑权值为ω1=0.1,ω2=0.1,ω3=0.8,ω4=0.8,ω5=0.1 的1-w-norm基准n维图表显示结果如图5所示。

图3 DTLZ1 Pareto前沿平行坐标系可视化展示Fig.3 DTLZ1 Pareto front parallel coordinates plot visualization

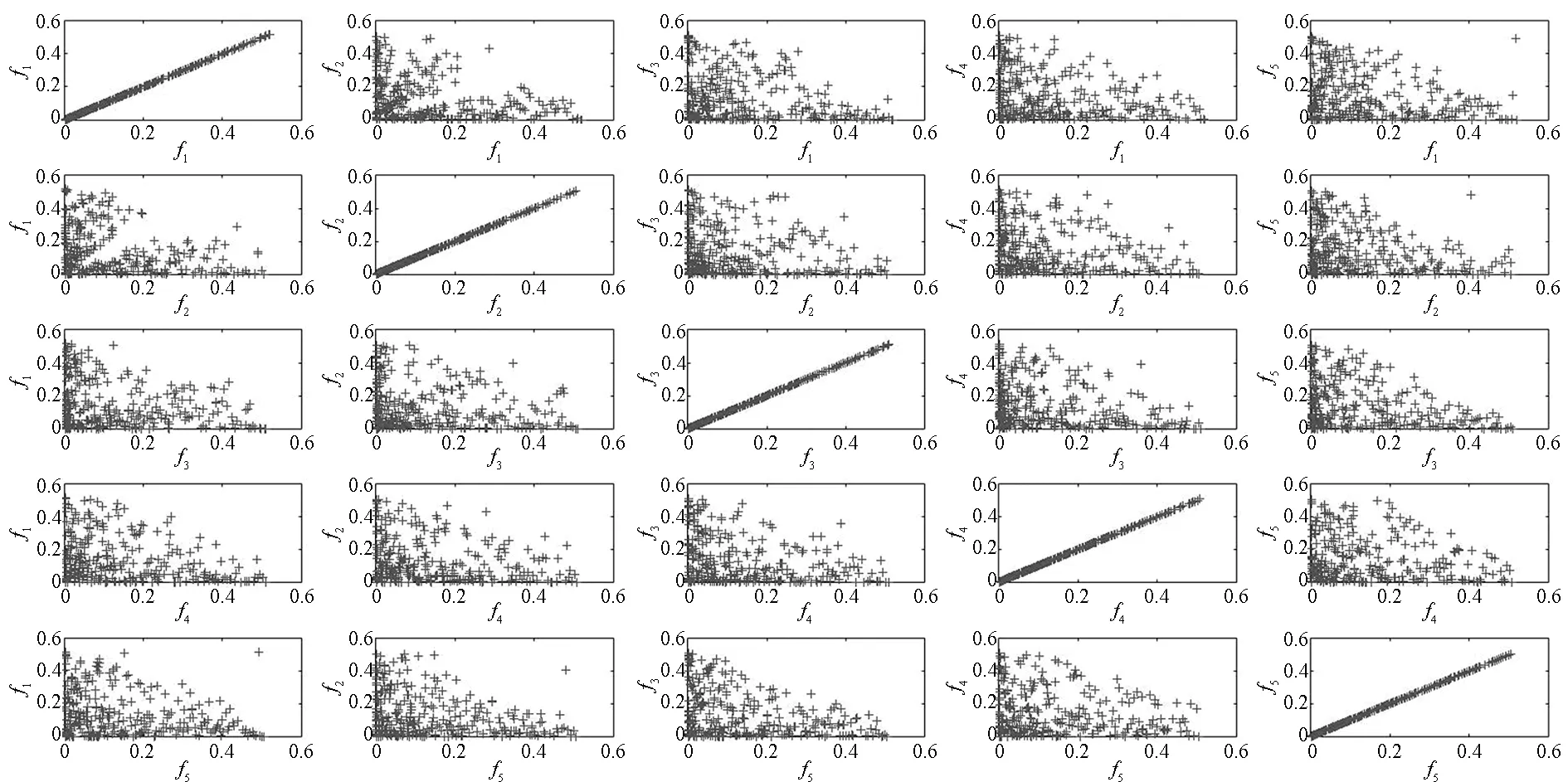
图4 DTLZ1 Pareto前沿散点图可视化展示Fig.4 DTLZ1 Pareto front scatter diagram visualization

图5 DTLZ1 Pareto前沿1-w-norm图表可视化展示Fig.5 DTLZ1 Pareto front 1-w-norm diagram visualization

由图3可以看出，最优解集的目标向量通过各轴之间的连线表示，决策者能够指定轴进行排序并通过颜色区分，例如f1的取值范围为0～0.5，其中浅色部分表示取值在0～0.05范围内分布密集。但是，浅色连线在其他子目标适应度函数上未呈现明显聚类特征。由于各连线交叉重叠，实际应用中决策者很难甄别出各方案的优劣。

图4将目标向量的各维度信息两两组合，绘制出20个二维图表。决策者需要分析目标向量在所有散点图表中的性能趋势。由于图表数量过多，势必会引起视觉混乱，无法有效辅助决策者进行分析决策。

图5通过目标函数的共享机制集成了基于权重的决策偏好信息，在某一权重明显大于其他权重时分层效果较为明显。本实验考虑分配权重ω1=0.1,ω2=0.1,ω3=0.8,ω4=0.8,ω5=0.1，以测试两类决策偏好共同作用的效果。由图5可以看出，f3、f4的取值虽然整体随纵轴递增而增大，但未形成明显的分层效果，无法继续筛选出合适方案。

图6为基于径向轴图的交互式n维Pareto前沿可视化效果，各径向轴表示实验算例的各子目标函数，在图6中由对应投影点表示，投影点在各轴上的分量表示其子目标估计值。将f2、f5轴调整为相互正交，并拉伸轴向量长度，表示当前决策偏好于f2、f5。其他轴旋转至其反方向，得到投影点分布情况如图6(a)所示，获得的最左下角点代表某方案f1=0.312 1,f2=0.004 3，f3=0.182 2,f4=0.186 3,f5=0.001 7。通过数据校验，该方案确实为最优解集中满足f2、f5最小的。将轴f3、f4拉伸并旋转至相近角度，其他轴缩小长度并旋转至相对正交的角度，得到Pareto前沿投影点集如图6(b)所示，表示偏好于f3、f4的最小化取值方

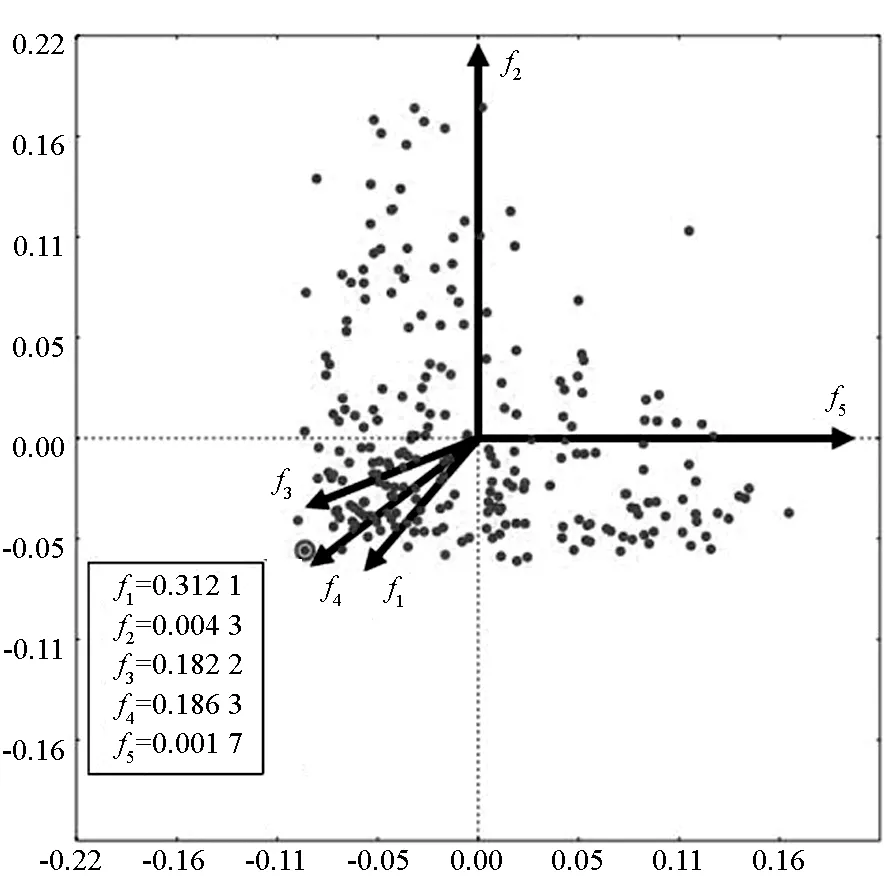
(a) 决策偏好于f2与f5轴的投影点分布(a) Projection point distribution of decision preference in f2 and f5 axises

(b) 拉伸f3、f4轴后的投影点分布(b) Projection point distribution after stretching of f3 and f4 axises

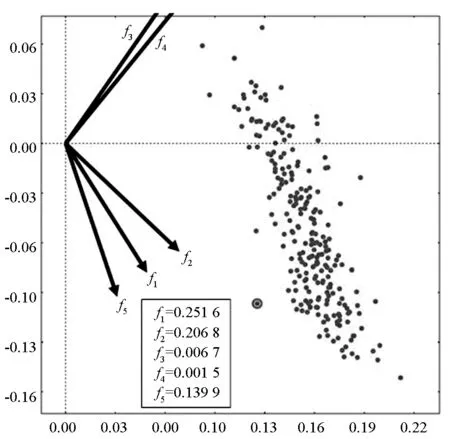
(c)图缩放后的投影点分布(c) Projection point distribution after scaling ofFigure(b)图6 基于径向轴图的交互式n维 Pareto前沿可视化效果展示Fig.6 Interactive visualization of n-dimensional Pareto front based on radial axes plots

案。由于投影点集分布情况比较密集，通过对整体视图的缩放和平移操作，得到投影点集分布情况如图6(c)所示。沿f3、f4轴方向寻找最低的一点，表示某方案f1=0.251 6,f2=0.206 8,f3=0.006 7,f4=0.001 5,f5=0.139 9。通过数据校验，该方案确实为最优解集中满足f3、f4最小的。实验证明，基于径向轴图的交互式n维Pareto前沿可视化决策方法效果直观有效。

5 结论

本文提出了一种基于径向轴图的交互式n维Pareto前沿可视化决策方法，解决了集成决策偏好的高维多目标可视化问题。通过实验与平行坐标系、散点图以及基于权重的n维图表等主流多目标可视化方法进行对比分析，证明了该方法能够以形象直观的方式呈现Pareto前沿各维度信息。基于径向轴图的交互式n维Pareto前沿可视化决策方法不仅有效集成了决策偏好信息，并且能够根据用户交互即时更新视图，辅助决策者正确把握目标性能趋势。并且，该方法易于实现，在数据挖掘、决策分析、任务规划以及多学科优化设计等领域都具有重要的应用价值。