固定翼无人机群的集群和避障控制*

伍友利，叶圣涛，方洋旺,2，朱圣怡，张丹旭

(1. 空军工程大学 航空工程学院， 陕西 西安 710038； 2. 西北工业大学 无人系统研究院， 陕西 西安 710072)

无人机群作战是一种全新概念的作战模式，对未来战争的影响将是颠覆式的。构成无人机群的无人机个体能力较弱，但若借助有效的集群控制手段，无人机群系统作为整体能够展现出强大的力量。

Tanner[1-3]等提出了分布式控制律来解决无人机集群飞行的问题，通过速度反馈项来实现速度匹配，基于人工势能场的位置反馈来实现聚集和避碰。Olfati-Saber[4]提出了采用虚拟Leader的反馈来保证系统的聚集，为每个相邻个体产生虚拟agent的方式来实现避障的方法。Su[5]等证明了文献[4]中所提算法在无障碍空间中的稳定性，并且提出了只有部分agent可以获取虚拟agent信息的集群方法。Dai[6]等将文献[4]中的算法扩展到了三维空间，并给出了对不规则立体障碍物的避障算法。Wang[7]等提出了一种多agent动态系统的快速避障算法，提高了系统速度一致的快速性，并且减少了能量消耗。

然而，大多数研究无人机集群控制的文章中，都是将无人机简化为一个具有二阶积分特性的质点来处理[8]，或者是假设无人机具有三通道自动驾驶仪，并且具有瞬时响应的能力[9]。这些假设都与实际无人机模型相差甚远，很难真正运用到实际的无人机集群控制中。因此，建立真实的无人机控制模型，推导无人机协同飞行制导律和协同控制律的联系就显得尤为重要。

本文首先采用质点模型，对传统的Flocking算法进行了改进，不再需要获取相邻个体的速度信息。然后将算法的计算输出转化为无人机飞行的跟踪指令，并采用某型无人机的三维六自由度小扰动线性化模型，通过设计合适的控制律，使得无人机群完成集群控制。

1 基于质点模型的Flocking控制器设计

1.1 质点系统模型

考虑三维空间中存在n个可以自由移动的质点和l个静态障碍物，每个质点的动力学系统抽象为二阶积分系统：

(1)

其中：第i个质点的位置记为qi=[xi,yi,zi]T，速度记为pi=[vix,viy,viz]T;ui=[uix,uiy,uiz]T表示第i个质点的控制输入。

假设无人机质点i的最大通信范围为R，最大检测范围为r，则定义如下信息域：

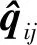
1.2 经典算法回顾

经典的集群控制算法是Olfati-Saber[4]在2006年提出的，具体的控制输入设计为：

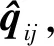
(2)

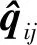
1.3 改进算法

为了改进经典的群集算法，简化其通信数据的交互，采用文献[10]中的思想，将邻域范围内的所有其他无人机都看作是障碍物，无须获得其速度信息，借用避障的算法，重新定义其他无人机的速度，然后通过构造光滑的势能函数，使得无人机群完成聚集的同时避免发生碰撞。

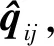
(3)

其中

(4)

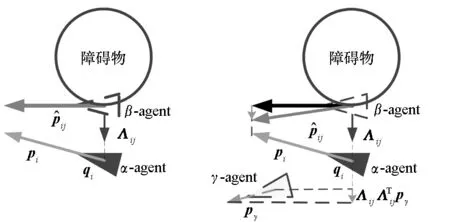
(a) 经典算法(a) Classical algorithm (b) 改进算法(b) Improved algorithm图1 经典算法与改进算法Fig.1 The classical algorithm and the improved algorithm

(5)

(6)

此外，为了简化文献[10]中所给的势能函数，重新定义有界势能函数U(z)为：

U(z)=U0(z)ρh(z/dσ)

(7)

其中

U0(z)=-dσ/(z+ε0)+ln(z+ε0)

ρh(z)和U(z)曲线如图2所示。

(a) ρh(z)

(b) U(z)图2 ρh(z)和U(z)曲线图Fig.2 Curves of ρh(z) and U(z)

可以看出：pij的计算不再需要检测范围内物体的速度，即不需要获取通信范围内无人机的速度信息，从而降低通信网络的负担。

2 稳定性证明

改进后的算法不再需要相邻无人机的速度信息，下面在缺少速度信息的情况下，讨论系统的稳定性。

定义集合：

定义无人机群系统能量函数：

(8)

其中

(9)

(10)

(11)

首先，考虑不存在障碍物的情况下，系统的稳定性。

定理1在不存在障碍物的空间下，由n个具有式(1)特性的无人机组成的系统，在式(5)的作用下，系统能量是非增的。

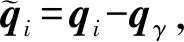
(12)

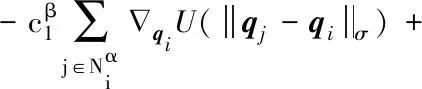
(13)

由于U和aij的对称性，则：

(14)

(15)

将式(14)代入式(12)，则：

(16)

由式(15)有：

□

下面考虑存在光滑凸形障碍物的情况。 其产生的β-agent的位置和速度如下。

如图3所示，对于球形障碍，其外形由球心yj和半径Rj所决定，当无人机靠近球形障碍时，其产生的β-agent的位置和位置导数为：

(17)

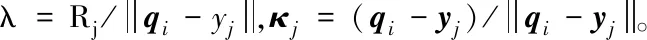
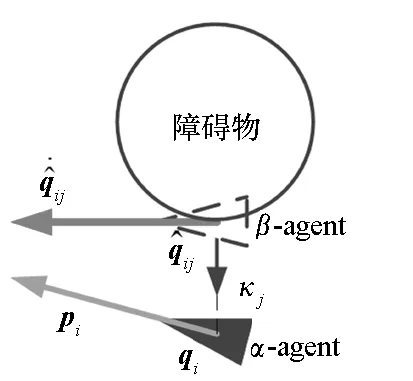
图3 光滑凸形障碍物Fig.3 Smooth convex obstacles

定理2在定理1的假设前提下，存在以上光滑凸形障碍物的空间中，如果满足：

(18)

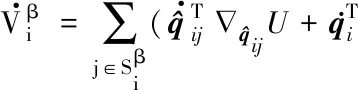
由式(7)的定义，得：

(19)

所以，根据式(16)和式(19)得：

(20)

又因为式(5)中的ui可以写为：

(21)

将式(21)代入式(20)，并结合式(3)得：

□

3 协同导航与控制

3.1 指令转换

为了将质点模型计算得到的控制量ui=(uix,uiy,uiz)T应用到实际的无人机模型中，首先要将期望的控制量转换为一系列实际指令[11]作为第i个无人机的期望速度Vic，期望俯仰角θic和期望偏航角ψic。

因此，定义第i个无人机的导引律为：

gci=[Vic,θic,ψic]T

3.2 无人机模型

根据文献[11-12]，本文选取某小型航模无人机进行运动建模，以“定常直线无侧滑飞行”为基准运动，将无人机的运动方程进行完全解耦，分别建立纵向运动平面和水平运动平面的六自由度小扰动线性化模型。则有：

(22)

(23)

其中变量含义及系统系数矩阵具体见参考文献[11]。

联立方程(22)～(23)，则无人机群系统可以写为：

其中，A=diag{Alon,Alat}，B=diag{Blon,Blat}，C=diag{Clon,Clat}。选取纵向状态(ΔV,Δθ)T为被控量，水平状态(Δψ,Δβ)T为被控量。其中令侧滑角的控制指令始终为0。

将被控量与无人机的基准运动状态相叠加，得到最终无人机的输出状态为y=[V,θ,ψ,β]T。则取系统的期望输出为yd=[Vc,θc,ψc,0]T。

定义系统的误差e(t)=Csy-yd，Cs是用来选择与yd一致的输出信号。为了保证系统在达到稳态时没有静态误差，引入跟踪误差的积分信号得到以下增广系统：

(24)

如果要保证系统式(24)完全可控，则必须满足：

其中,n、p分别为矩阵A、CsC的阶数。

根据文献[13]的内容，当系统完全能控，则必定存在反馈系数矩阵K=(K1,K2)，使得系统矩阵的所有特征根都具有负实部，则设计控制器的输入为：

从而状态反馈控制器为：

(25)

4 仿真分析

4.1 质点模型仿真

首先针对质点模型，分别考虑有障碍物的空间和没有障碍物的空间，构建如图4所示仿真编队系统。30架无人机质点的初始位置和初始速度随机生成，虚拟无人机质点做匀速直线运动。其余仿真参数见表1。

表1 质点模型仿真参数

根据表1中所给参数，分别在无障碍物空间和有障碍物空间中进行仿真，如图5所示，无人机质点可以按照虚拟无人机的飞行，保持集群飞行而不会发散，说明算法在无障碍物空间下飞行的稳定性。在有障碍物空间的飞行时，无人机在保持集群飞行时遇到障碍物，先分散后再集群，可以有效地避开障碍物，并且在避开后迅速地形成集群编队，跟踪虚拟无人机的飞行。

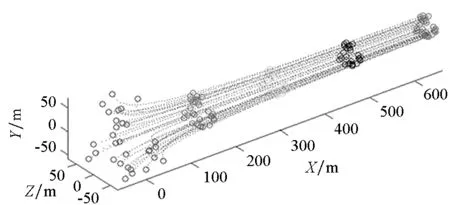
(a) 无障碍物空间(a) Free-space

(b) 有障碍物空间(b) Obstacles-space图5 质点在无障碍空间和有障碍空间的飞行轨迹Fig.5 Flight path in the free-space and obstacles space

图4 编队系统框图Fig.4 Structure of formation system

图6为无人机质点在飞行过程中，无人机之间的最短距离及其与障碍物之间的最短距离，从图中可以发现，在整个飞行过程中，无人机之间没有发生碰撞，保证了飞行的安全性。无人机群有效地避开了障碍物，进一步验证了算法的有效性。

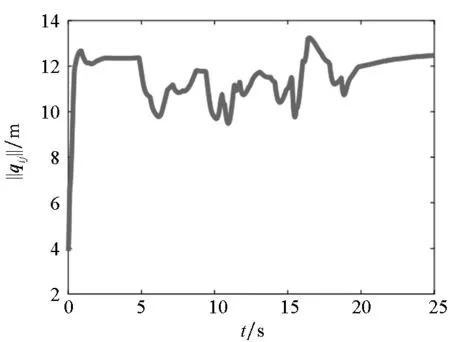
(a) 无人机之间的最短距离(a) The minimum distance among UAVs

(b) 无人机与障碍物之间的最短距离(b) The minimum distance between UAVs and obstacles图6 无人机与障碍物及其相互之间的最短距离Fig.6 The minimum distance from UAV to obstacles or nearby UAVs

4.2 六自由度无人机编队控制仿真

下面采用更加贴近实际的六自由度无人机进行仿真验证，首先由质点集群算法求取飞行指令作为导引指令，然后利用跟踪控制器来跟踪指令，无人机的最大飞行速度为32 m/s；最小飞行速度为7 m/s。无人机的升降舵δe=±25°，方向舵δr=±30°，副翼δa=±40°。忽略无人机之间的通信延迟，仿真所用的其他参数见表2。

图7～8为六自由度无人机集群飞行仿真结果。图7为6架无人机的飞行轨迹及其各指令的跟踪情况。可以看出，无人机可以形成集群编队并且有效避障；并且实际的无人机编队的速度、偏

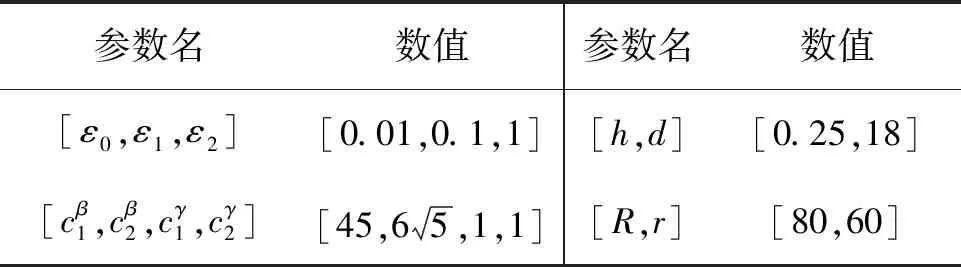
表2 六自由度无人机编队仿真参数

航角、俯仰角能够很好地跟踪给定的指令信号；图8分别给出了油门开度、升降舵、方向舵和副翼的变化规律，其变化大小、变化范围都在实际无人机性能范围内。从而说明了基于本文所给出的六自由度无人机编队控制方法的有效性。

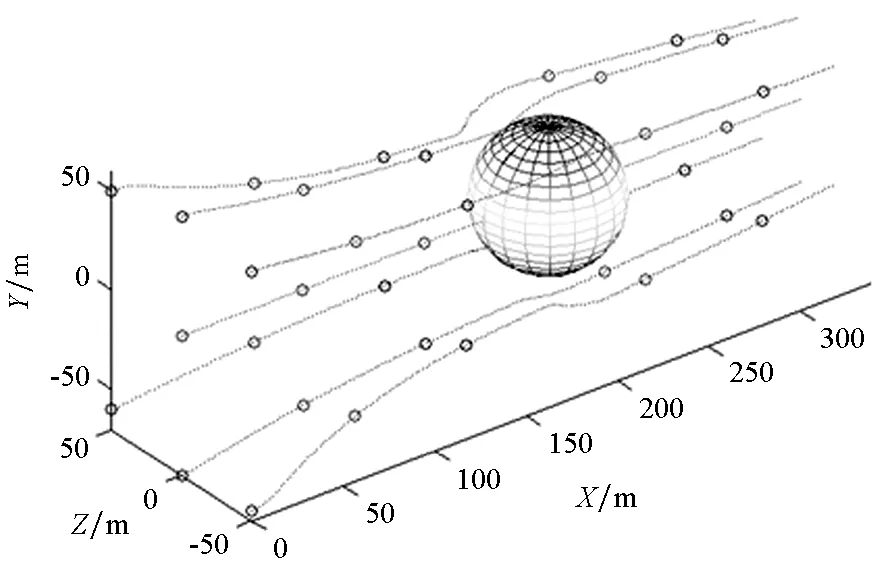
(a) UAV飞行轨迹(a) UAV flight path

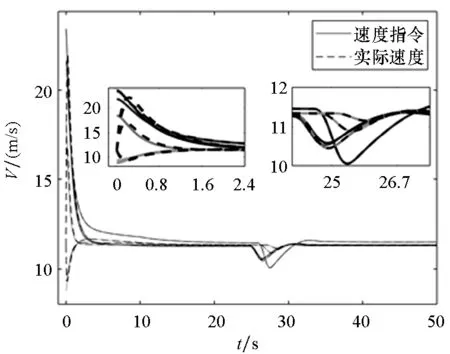
(b) 速度跟踪曲线(b) Velocity tracking curve

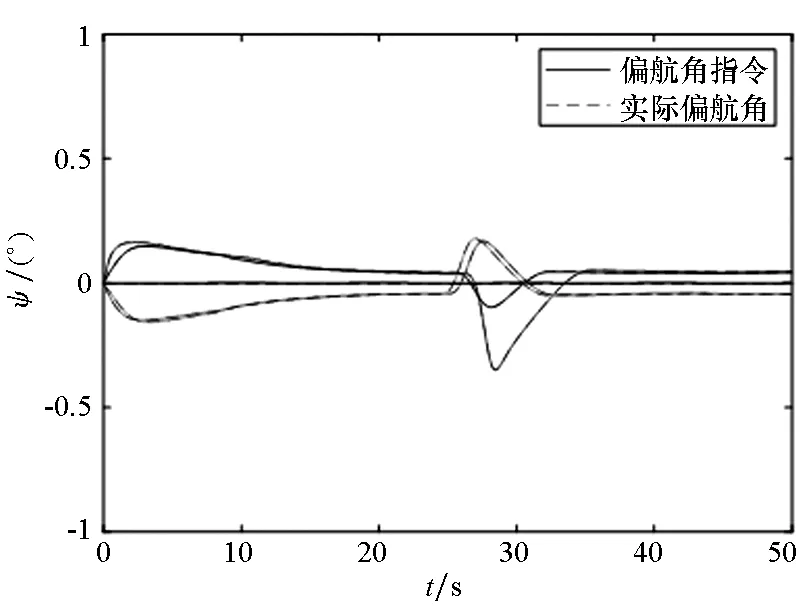
(c) 偏航角跟踪曲线(c) The yaw angle tracking curve

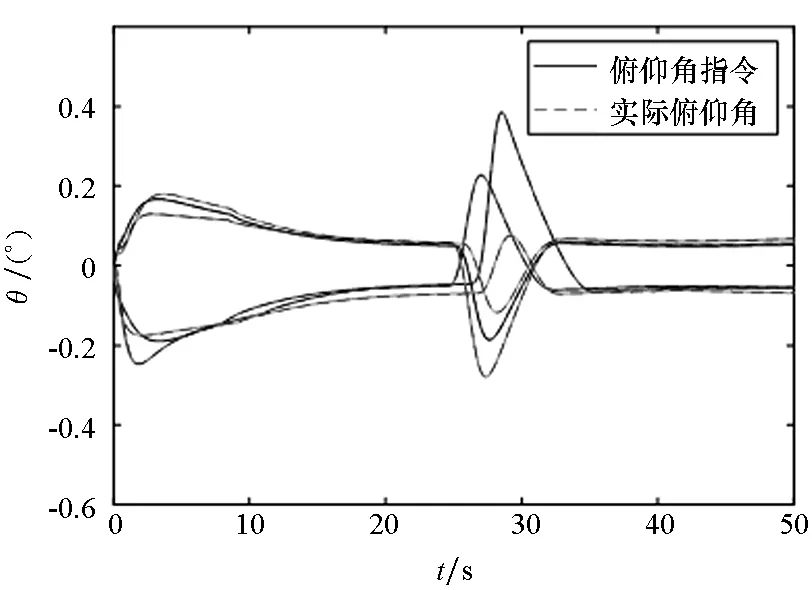
(d) 俯仰角跟踪曲线(d) The pitch angle tracking curve图7 无人机轨迹和指令跟踪曲线Fig.7 Flight path and commands tracking of UAVs

(a) 油门开度曲线(a) The throttle opening curve

(b) 升降舵输入角度曲线(b) The input angle of elevator curve

(c) 方向舵曲线(c) The rudder angle curve

(d) 副翼输入曲线(d) The aileron input angle curve图8 无人机输入曲线Fig.8 Input of UAVs

5 结论

针对传统的多智能体群聚算法需要领域范围内无人机的速度信息，以及在避障时需要区分所检测到的无人机是否为障碍物的问题，本文提出了一种改进的无人机质点集群算法。通过将领域范围内所有无人机等效为障碍物的思想，无须获得相邻无人机的速度信息，通过相对位置信息重新定义无人机的速度，从而直接计算控制输入。然后将质点集群算法的控制输入转化为无人机真实的控制指令，采用小型固定翼无人机的六自由度小扰动线性化模型，设计无人机集群的跟踪控制回路，使得无人机群能够实现集群控制。但文中无人机之间的通信状态为理想状态，并未考虑其延迟、丢包等实际情况。另外，由于改进的算法没有使用速度信息，当无人机之间的初始速度相差较大，或者有个别无人机的速度非常大，这种情况下将会影响系统的收敛时间和避碰的有效性。因此，设计更加优化的算法和考虑通信数据链在非理想状态下的无人机集群控制将是下一步的研究工作。