扩张状态观测器的观测误差前馈补偿设计*

高钦和，董家臣

(火箭军工程大学 兵器发射理论与技术军队重点实验室， 陕西 西安 710025)

在非线性系统的控制中，使用状态观测器估计系统状态以实现前馈、反馈、解耦或补偿是一种实用而有效的控制思想。韩京清等提出的自抗扰控制(Active Disturbance Rejection Control, ADRC)技术[1-3]通过设计扩张状态观测器(Extended State Observer, ESO)，在不依赖扰动模型的前提下能够实时观测系统“总扰”并反馈补偿控制率，具有极强的扰动抑制能力。ESO作为ADRC的核心，通过观测误差方程的迅速收敛实现对系统各阶状态的跟踪，然而采用的误差非线性收敛形式fal(e,α,δ)在获得高观测效率的同时也带来了参数整定烦琐的弊端。为此，Gao等[4]基于带宽思想将ADRC的控制器和ESO均以线性形式实现，将需整定的参数由7个以上减少至2个，使得线性自抗扰控制器的广泛工程应用成为可能。

在构建ESO时采取了忽略扰动的处理方式，故在扰动存在动态变化的情况下观测将存在误差。利用非线性函数的“大误差、小增益，小误差、大增益”特点可以有效减小这种观测误差的影响。而线性扩张状态观测器(Linear Extended State Observer, LESO)为了获取更简便的参数整定效率放弃了非线性形式，在观测精度上不得不做出让步[4]。作为反馈补偿的输入源，LESO观测误差的存在会降低伺服系统的控制精度，因此在光刻机、高精度数控机床等精密领域，线性自抗扰控制(Linear ADRC, LADRC)技术的应用相对受限。提高LESO的观测精度成为LADRC研究的热点之一。

当前，许多学者已经对LESO的观测能力展开了研究。文献[5-7]在时域内给出了被控对象动态模型未知时观测误差有界的理论证明；文献[8]对二阶系统LESO收敛性和频带特性和滤波性能进行了分析，并通过仿真进一步分析了LADRC的稳定性和抗扰性；文献[9]则使用频域分析法分析了LESO的跟踪性能，通过非“3w”法参数整定原则对LESO做出了改进；文献[10]证明了高阶LESO的收敛性，通过仿真得出增加扩张阶数和提高带宽均能提高观测精度的结论。

LESO的滤波能力、观测误差的收敛性和有界性、观测系统的稳定性等性质已经得到了较多的研究证明，然而在如何有效提高观测精度上，尚缺少文献进行策略设计并给出理论分析。然而，在实际应用中，往往更需要对LESO的观测误差有一个量化的表述，以据此做出相应的改善，增强观测器的跟踪能力，并最终提高整个LADRC系统的控制效果。在这一方面的研究中，目前只有文献[11]做出了尝试，提出使用误差的多阶微分改进ESO的策略，但这种方式本质上变更了经典ESO的结构，因此传统ESO的稳定性研究成果不再适用，为此该文给出了二、三阶ESO的稳定证明，但对更高阶的观测器则未进行讨论；同时误差项的多阶微分的使用并不适用于含噪声的系统，这也限制了这种改进策略的使用。

为此，本文从分析LESO的观测机理入手，通过对扰动项的线性化、误差系统动态响应的忽略，推导出LESO观测静差的量化表达形式，并据此提出了一种前馈补偿器。随后从理论上分析了补偿思路的可行性，对误差幅值和相位滞后的补偿效果分别进行了讨论，进而将这种补偿思路扩展至NESO中，最后通过仿真和实验对补偿器的有效性进行验证。

1 ESO的设计简介

不失一般性，考虑如下一类单输入单输出(Single-Input-Single-Output， SISO)的非线性时变系统：

y(n)(t)=f(y(n-1)(t),…,y(t),w(t))+bu(t)

(1)

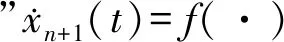
(2)

其矩阵形式可表达为：

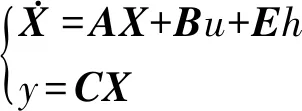
(3)

在h未知、干扰模型无法利用的前提下，按照ESO的设计思路[1]，采取忽略扰动的处理方式，建立式(4)所示观测模型：

(4)

式中：zi(t)为xi(t)的观测值(i=1,…,n+1)，βi为ESO的增益系数，gi(e1(t))代表设计的误差函数。由系统模型(2)与观测模型(4)作差，可以得到观测误差系统：

(5)

式中，ei(t)=xi(t)-zi(t)。当e1(t)gi(e1(t))>0,∀e1(t)≠0且gi(0)=0时，误差系统(5)是渐近收敛的[10]。此时模型(4)能够以一定精度实现对模型(2)各阶状态的跟踪。可通过调整βi来调整误差收敛的速度，以获得期望的观测效果。目前，对于gi(e1(t))主要有两种设计方法：

1)非线性函数。经典连续幂次函数fal(e1,α,δ)应用较多，其形式为：

(6)

式中：α表示放大因子，δ表示原点附近线性区间长度。该函数具有“大误差、小增益，小误差、大增益”的收敛特点，线性段的引入能够有效减轻高频颤振现象，以此构造的非线性扩张状态观测器(Nonlinear ESO, NESO)，在观测上具有误差衰减快、观测精度高、观测带宽实时自调整等显著优势，但在实际应用中，参数整定复杂、稳定性分析也较为困难。

2)线性函数。最简线性函数可取gi(e1(t))=e1(t)，此时模型(4)中的观测部分可列写为式(7)所示矩阵形式：

(7)

(8)

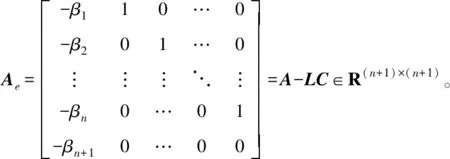
求出其特征方程f(λ)，并基于文献[4]的带宽整定思想配置观测增益：

f(λ)=|Ae-λIn+1|=(λ+wo)n

(9)

式中，wo∈R+为设置的观测器带宽。通过这种方式配置L使得式(9)满足Lyapunov第一稳定条件，即可使LESO以一定精度实时跟踪系统状态。至此，对任意阶数的LESO均只存在一个待整定参数wo。LESO设计简单，时域、频域分析理论均可使用，同时参数整定过程较NESO得到极大简化，这使得LESO的广泛工程应用成为可能。因此后文以LESO为主要研究对象展开分析。

2 LESO的观测误差分析

LESO是LADRC的核心部分，其估计精度和速度决定了扰动补偿的效率，直接影响整个系统的控制效果。由于系统总扰项在动态变化时存在不确定性和非线性，观测误差的直接计算存在一定困难。文献[6]指出，在h(t)有界时，按式(7)构造的LESO观测误差是一致收敛的，同时给出了误差的有界性证明。在此前提下，如果能进一步将观测系统做线性处理，就可以使用成熟的线性系统分析理论对观测误差做量化分析。

2.1 误差系统的线性近似

2.1.1 总扰项的线性化

假设总扰项f(y(n-1)(t),…，y(t),w(t))各阶导数存在且有界，在t0时刻对其泰勒展开：

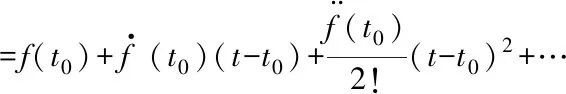
=f(t0)+h(t0)(t-t0)+ο(t-t0)

(10)

类比微分，在观测步长Δt=t-t0足够小，近似误差ο(Δt)可忽略时，可以将未知扰动按线性变化来处理。因而在分析误差系统时做以下近似：

近似1：在计算步长Δt内，视h(t)=h(t0)=h0为恒值。

这种近似产生的截断误差不会超过：

(11)

此时，在Δt内误差方程(8)变为常系数一阶线性非齐次矩阵微分方程：

(12)

2.1.2 误差动态响应的忽略

将式(12)展开，得到误差微分方程组:

(13)

可见，各阶误差在误差系统中相互嵌套，同时存在着动态响应和稳态静差。动态响应影响观测速度，静差大小则决定LESO最终观测精度的高低。动态响应的客观存在使得量化表示某一时刻的观测误差十分困难。

注意到式(9)中基于带宽wo的参数整定方法使得式(12)中系数矩阵Ae是Hurwitz的、误差方程能够实现渐近稳定，即

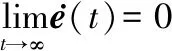
(14)

这意味着随着时间的推移，误差的动态响应分量在LESO的观测误差中所占比重将逐渐减小，直至最终无限趋近于0。因此将式(14)代入式(12)中能够得到：

(15)

误差(15)即为最终的稳态观测静差。然而对控制系统而言，严格满足t→∞这一收敛条件是不实际的。事实上，LESO观测误差的收敛速度由带宽wo决定，在不考虑噪声引入的情况下，wo越大，对应的收敛速度越快[8,10]。在实际应用中，通过整定wo实现对系统各阶状态的迅速观测是保证观测系统正常发挥作用的前提。因而在此基础上做出进一步的近似，认为在计算步长Δt内式(12)已能达到稳态。

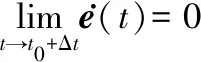
经过以上近似，在单次计算步长内可以将动态响应略去，使用式(16)来描述LESO的观测精度：

(16)

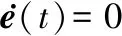
2.2 观测误差的表达

对式(16)展开并化简，得：

(17)

按照带宽配置原则，由二项式定理可得观测增益：

(18)

将其代入式(17)并化简，得到观测静差的最终表达式：

(19)

至此，通过近似1、近似2，将LESO的误差系统进行了线性处理，极大地简化了时变系统中扰动项的非线性和LESO观测误差收敛过程中的动态响应带来的分析困难。在此基础上推导出的静差表达式(19)，即可认为是近似后LESO的观测误差量化表达式。

结论1：LESO在本质上属于有差观测系统，忽略f的构造方式使得观测过程存在如式(19)所示的近似观测误差，其大小与整定的观测器带宽wo、扩张阶数n以及总扰变化率h有关。在LESO阶数确定时，总扰变化过快将使得LESO观测精度降低，而提高带宽wo是提高观测精度的有效办法。

注2：实际应用中，受观测噪声的影响，wo的整定存在上限，此时，总和扰动变化较大的系统，误差的动态响应也会相对剧烈，近似2由于忽略误差的动态响应带来的偏差也会越大。因此，将静差表达式(19)看作LESO的观测误差量化表达式，对于扰动变化极为剧烈、LESO无法及时完成观测的系统而言并不适用。

3 LESO的前馈补偿设计

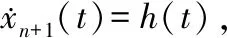
(20)

LESO的目标是实现对被观测系统各阶状态的实时估计，该过程依赖e1(t)的收敛，而e1(t)=x1(t)-z1(t)是可以实时获得的。为避免微分，做以下代换：

(21)

将其代入补偿器的表达式(20)中化简，并补充定义β0=1，补偿器最终可以用式(22)表达(Di表示第i阶状态对应的观测补偿量)：

{Di=βi-1e1i=1,2,…，n+1}

(22)

LESO的前馈补偿结构如图1所示。

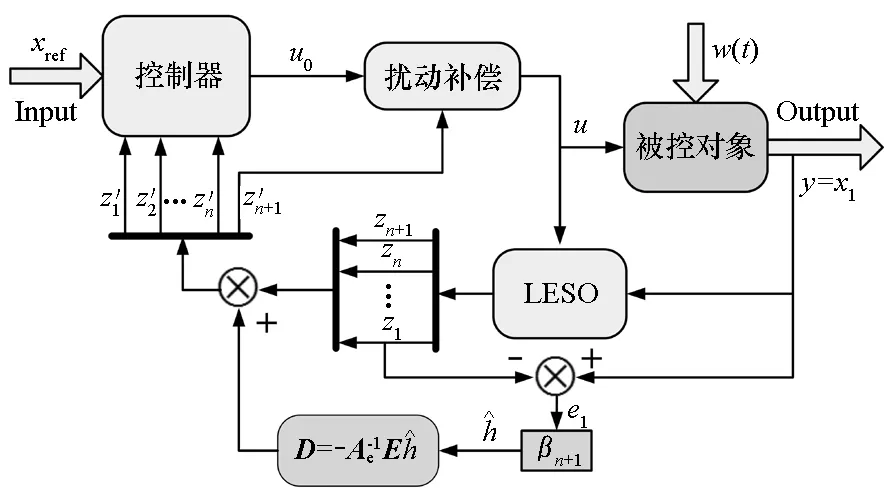
图1 LESO的前馈补偿结构设计Fig.1 Design of feedforward compensation structure of LESO

3.1 前馈补偿的时域有效性

由式(3)、式(7)、式(20)可得补偿后的误差方程：

后一项展开后为零矩阵：

(24)

故将Ae展开代入并继续化简，得到：

(25)

联立误差微分方程组(13)，最终可化简为：

(26)

结合第2节中所做的近似，最终能够得到：

(27)

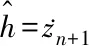
式(26)中，即便观测误差未及时收敛，恒有e′1=0。这正是使用e1补偿各阶观测误差的特点。由于LESO采用借助e1构造误差收敛系统的结构形式，基于可测真值y=x1修正观测值z1，同时也实现了对其他各阶观测量的修正。

3.2 对观测滞后的补偿作用

LESO的观测存在相位滞后，且观测器阶数越高，滞后越严重[9]。补偿器使用e1前馈补偿各阶状态，使得输入量与补偿后的输出量之间的传递关系发生了变化。接下来对补偿前后观测系统的时延做分析。

对模型(13)取拉式变换，化简后可以得到：

(28)

特别地，联立模型(28)中的最后两个公式，可以推导出扰动项与n+1阶观测误差之间的传递函数：

(29)

按照同样的分析方式，求出补偿后模型(26)的拉式变换式为：

(30)

将式(28)与式(30)联立，得到引入补偿器后LESO在观测第i阶状态时，补偿前、后观测误差之间的传递函数：

(31)

若采用式(18)所示的基于带宽的参数整定方式，并定义相对频率Ω=ω/ωo，可进一步化简出：

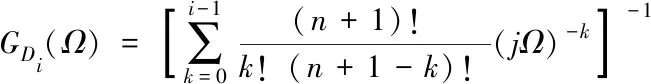
(32)

据此绘制出误差传递函数的Bode图(以4阶观测器为例)，如图2所示。

图2表明，各阶状态的观测误差经过补偿器的传递，幅值减小、相角滞后有所减轻，且这种补偿作用随频率的降低、观测的状态阶数的增高而更加明显；在Ω=5.128 6时，A(Ω)=1.43,φ(Ω)=43.592 9°，此时对各阶状态的补偿曲线已基本重合，补偿作用较为微弱；在Ω>13.3的高频区，|A(Ω)|<0.1，φ(Ω)<17.52°，此时补偿作用几乎丧失。当然，由于观测带宽存在上限，通常无法达到如此高的相对频率，因此补偿器在LESO的工作区是能够正常发挥作用的。

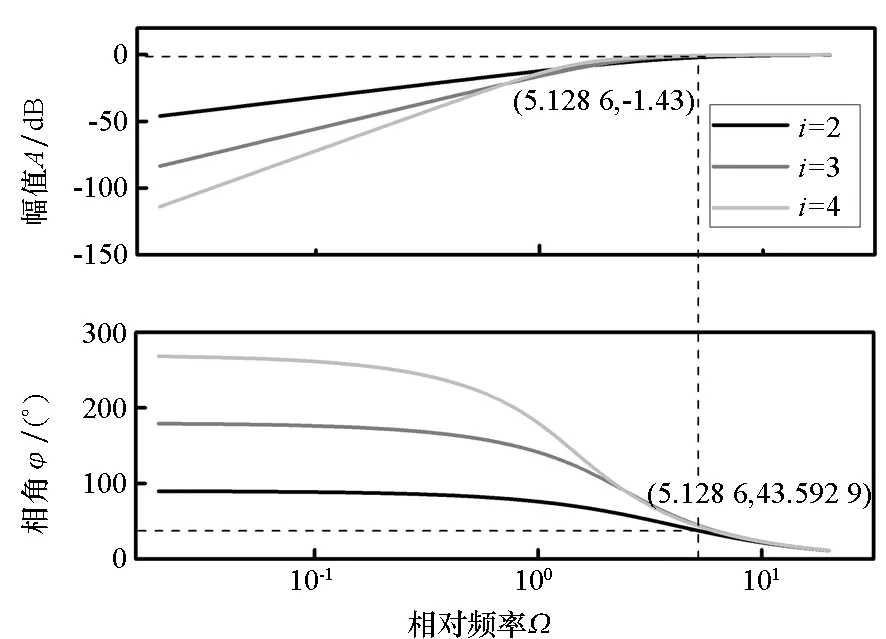
图2 误差传递函数的Bode图Fig.2 The Bode diagram of error transfer function

注3：补偿器以串联形式对观测值加以修正，并不影响LESO原有的收敛性、频带特性和滤波性能等固有性质。若通过整定观测增益，使得原系统的观测器满足BIBO(bound-in-bound-out)稳定[6-7]，此时在步长Δt内，对于系统第一阶状态的观测，下式是成立的(es指观测静差值)：

由补偿器的结构形式(22)可知，此时各阶补偿量同样是收敛且有界的，因此补偿环节的引入并不会造成观测系统的发散，即：补偿器与扩张状态观测器具有相同的稳定性，二者通过串联作用，共同实现对系统状态的无静差观测。

4 推广至NESO

LESO的结构特点使得通过线性近似后可以量化系统的观测静差，并可使用时频分析方法验证前馈补偿器的有效性；而对NESO，误差收敛选用的是非线性函数，不仅在推导观测静差上存在困难，频域分析法也无法使用。

图3给出了对LESO进行前馈补偿的过程示意。对比可见，经过前馈补偿，状态观测的综合过程已不存在误差项，补偿后的模型与真实系统形式相同，即便e1→0不成立，仍然不会存在观测静差。传统LESO通过误差系统的渐近收敛性提供观测驱动力，补偿器D则依据真实输入值y对各阶观测偏差进行实时修正。将这种补偿思路类比至NESO，有:

(33)

因此前馈补偿器应该取如式(34)所示形式(同样补充定义：g0(e1)=e1)：

{Di=βi-1gi-1(e1)i=1,2,…，n+1}

(34)

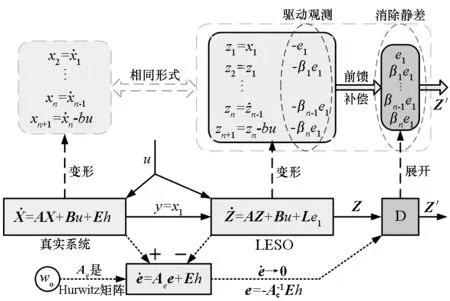
图3 补偿过程示意Fig.3 Compensation process

5 仿真与实验

本节分别通过仿真和实验验证补偿器的有效性。设计仿真系统，对各阶状态的观测误差补偿效果进行分析，同时比较补偿器对LESO和NESO的补偿能力。实验则重点考虑在整个LADRC系统中引入补偿器对控制精度的改善作用。

5.1 仿真

在参考文献[11]的基础上，设计如下含随机扰动的三阶非线性系统：

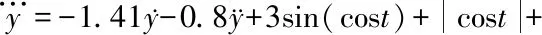
v(t)+4·u(t)

(35)

1)LESO按带宽整定思想配置，wo=100 Hz。

① LESO:

(36)

② D：

(37)

2)NESO的误差收敛函数取为fal形式，具体参数设置如下：δ=0.05，β1=40，β2=8×103，β3=8×104，β4=3×106。

① NESO:

(38)

② D:

(39)

图4～6详细给出了补偿器作用效果的仿真曲线。图4中横向对比可以发现，在补偿上D对x1实现了完全补偿，对x2、x3观测精度也存在两个量级的提升，补偿作用非常明显。通过纵向对比，不论是使用LESO还是LESO+D，均存在观测状态的阶数越高精度越低的规律，且各阶状态观测误差的曲线形状相似，任意时刻误差之间的比值与观测器增益近似一致(补偿后e1除外)。这是因为观测器在结构设计上使用e1构成误差收敛项，补偿前状态观测值与真值间的各阶误差必然按βi的比例递增，补偿后由于算例中扰动项的非线性特征较为明显，同时带宽wo的取值并不大、误差动态响应在单步计算中不能完全忽略，所以仍存在部分残留静差以及动态响应误差。随着带宽的增大，这部分误差可以继续减小。

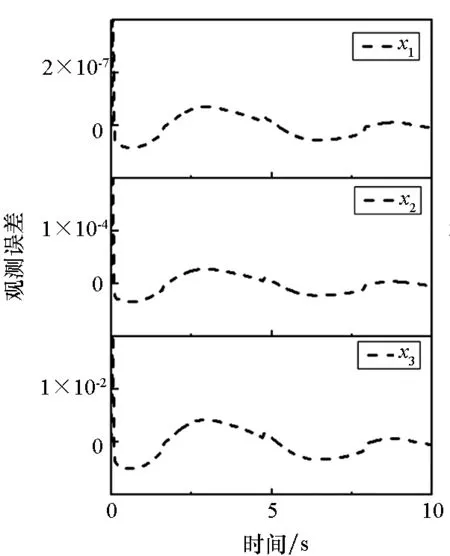
(a) 补偿前(a) Before compensation

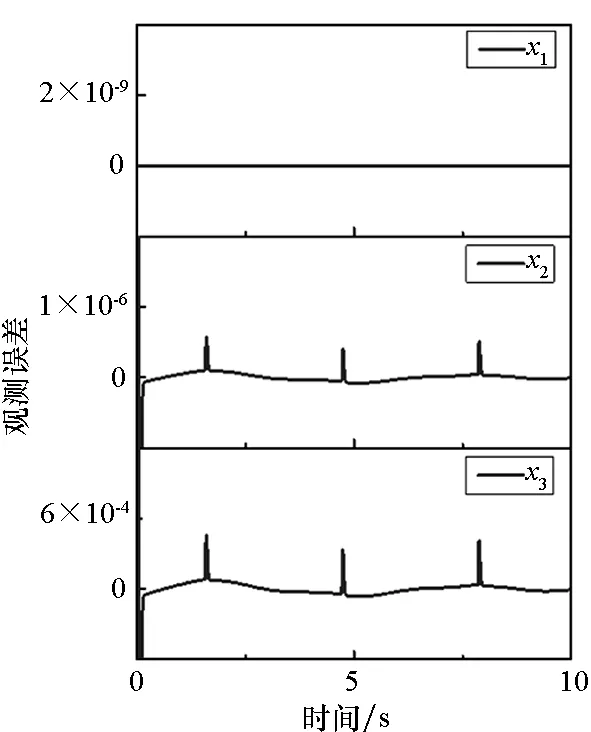
(b) 补偿后(b) After compensation图4 补偿前后LESO对各阶状态的观测误差对比Fig.4 Comparison of observation error of LESO for each order state before and after compensation

图5表明，在对x2的观测补偿上，稳定后最大观测误差LESO由2.839E-5减小至8.046E-8，NESO由4.38E-5减小至5.76E-7，精度均获得了百倍左右的提高。5 s加载扰动后，补偿器对状

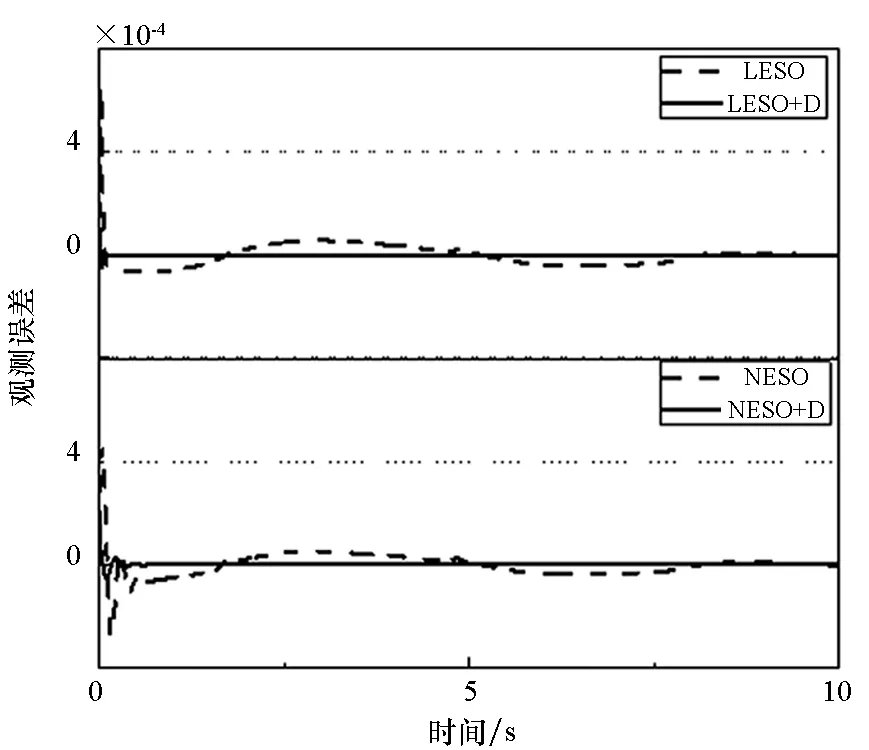
(a) v(t)为0(a) v(t) is set to zero

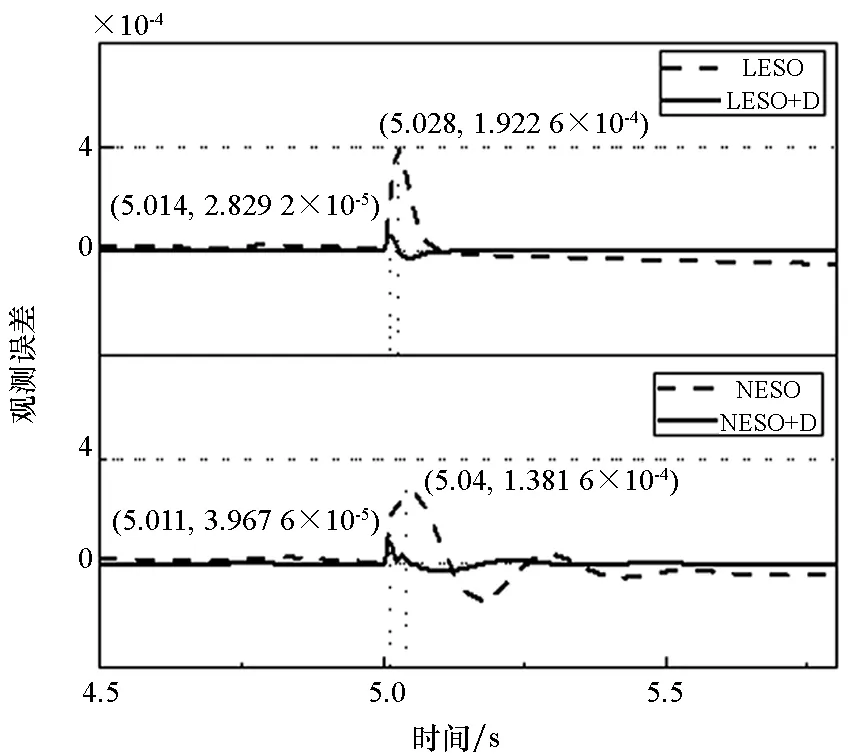
(b) v(t)为阶跃信号(b) v(t) is set to step signal

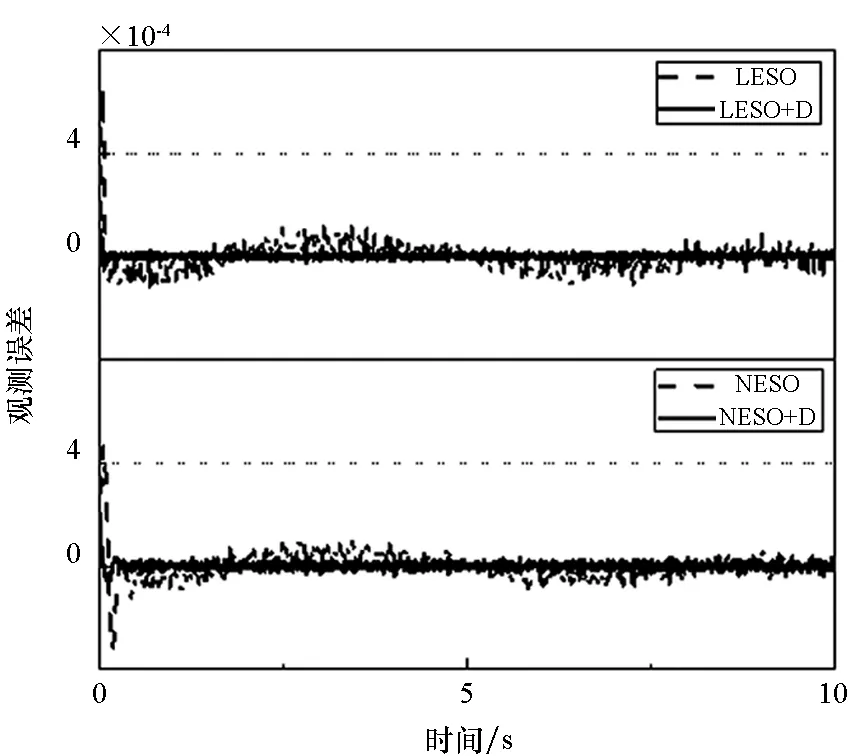
(c) v(t)为噪声信号(c) v(t) is set to noise signal图5 补偿器对x2的作用效果Fig.5 Effect of the compensator on x2

态的瞬时观测则只提升了约10倍，这是因为在扰动加载的瞬间，系统的非线性特征很强，补偿器完全补偿静差的两个近似条件不能严格满足，因此效果较图5(a)中的精度提升有所下降。图5(c)中系统存在噪声扰动的情况下，在提高观测精度的同时，观测器对噪声还产生了一定的滤波作用。在观测器的比较上，本文仿真中整定的参数使得LESO与NESO的观测精度相仿，但NESO的观测增益却比LESO小两个量级，这有力地证明了NESO在观测上的高效性。在图6中对x3的观测，LESO+D的观测滞后程度明显优于LESO，这与前文补偿器对相位滞后存在校正作用的推导是一致的。

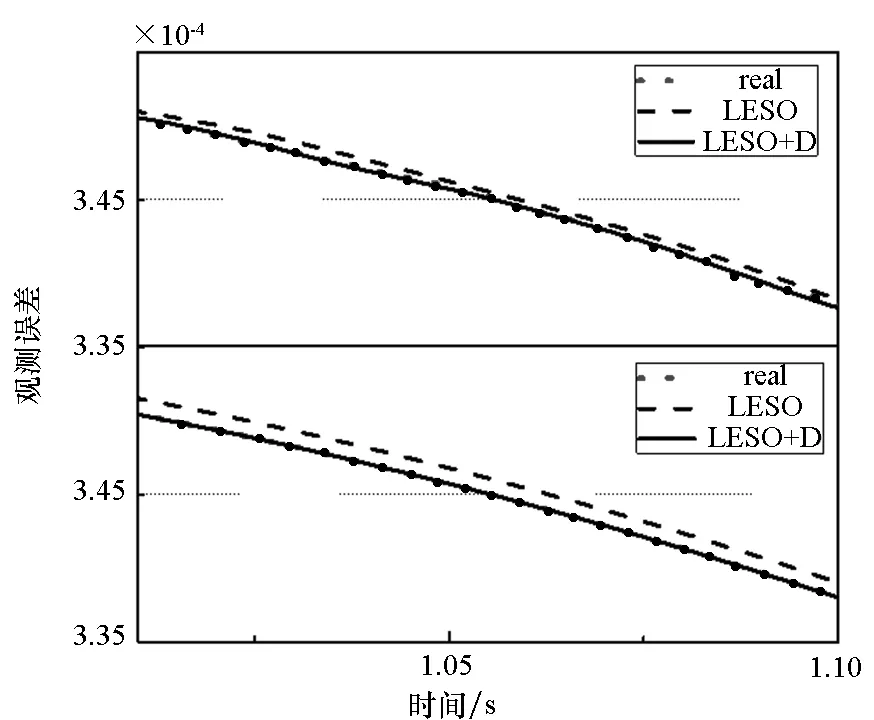
图6 对x3相位滞后的校正Fig.6 Correction of x3 phase lag

5.2 实验

ESO通常作为ADRC的一个重要环节，在实际应用中更关心的是补偿的设计对整体控制精度是否有提高。为此，针对PMLSM易受扰动影响而精度不高的问题，引入补偿器改进直线电机的LADRC伺服回路。系统中存在的纹波力、摩擦力、负载力等多种非线性扰动成为制约控制精度的主要原因。

直线电机的位置模型为二阶非线性系统[13]，引入补偿器后的改进LADRC控制系统设计如图7所示。

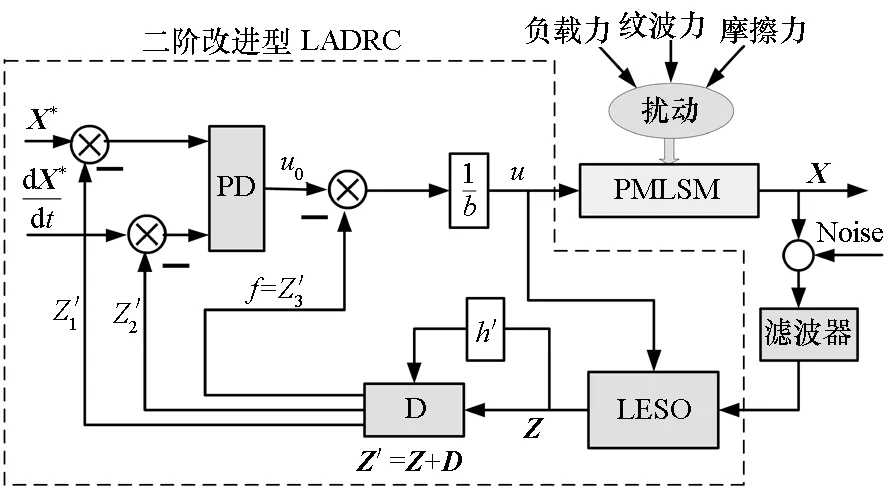
图7 改进LADRC在PMLSM控制中的结构图Fig.7 Structure of improved LADRC in PMLSM control

实验中使用了定制的永磁直线同步电机半实物仿真平台。在上位机中利用MATLAB/Simulink的XPC Target系统模块导入Simulink模型，经编译后下载至运动控制卡中，输出信号送入伺服驱动器以控制电机运行，采集数据并处理绘图。驱动器系数Ka=0.84 A/V，力常数Km=15 N/A，小车与砝码的总质量M=3.8 kg，摩擦力系数B≈1.2 N·s/m。电机行程1.0 m，光栅尺定位精度为±2 μm。

实验中，伺服系统控制参数最终确定见表1。

在上位机的MATLAB/Simulink中搭建图7所示的控制系统，利用RTW工具箱自动生成C代码，编译、下载到目标机。为同时验证补偿器对误差幅值大小、相位滞后的补偿有效性，期望信号设成频率为1 Hz、幅值0.1的正弦时变信号y=0.1sin(t)，过程持续10 s。

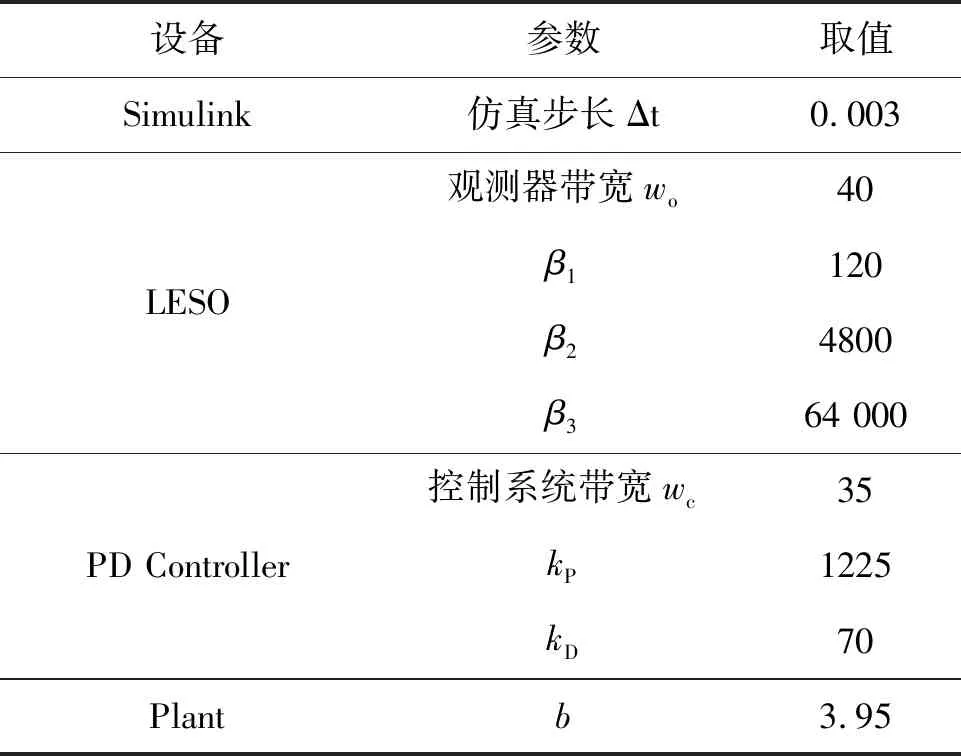
表1 改进LADRC测试系统参数设置

图8给出了实验中补偿器对动子位置的控制误差的作用效果曲线。由图可以看出，在追踪正弦时变信号时，补偿器对控制精度有明显提高。位置追踪在相位上得到了校正，且最大追踪误差由41 μm补偿至9 μm(见图9)，这是因为传统LESO始终将总扰变化率按h=0处理，对于时变信号这种处理方式带来的观测静差是无法避免的。引入补偿器后，观测静差得到了补偿、LESO反馈至控制器的观测量精度提高，这使得系统的控制输入更准确，因而LADRC系统的整体控制精度得到了整体提高。

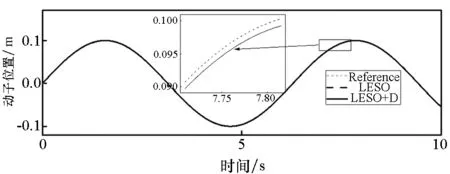
(a) 动子位置控制曲线(a) Position control curves

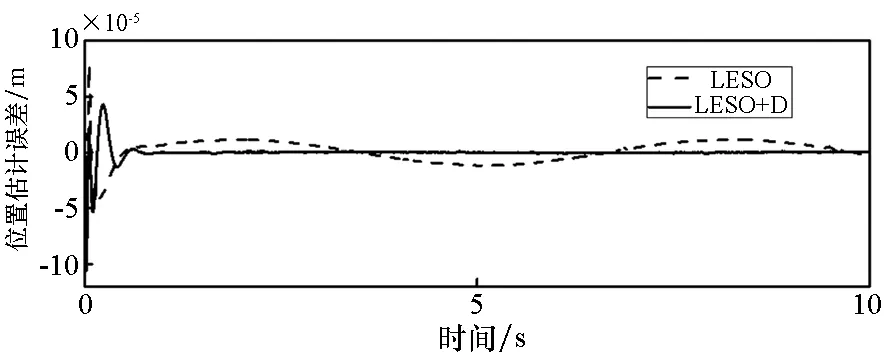
(b) 位置控制误差曲线(b) Position control error curves图8 补偿器在PMLSM实验平台中的应用效果Fig.8 Application effect of compensator on PMLSM experimental platform

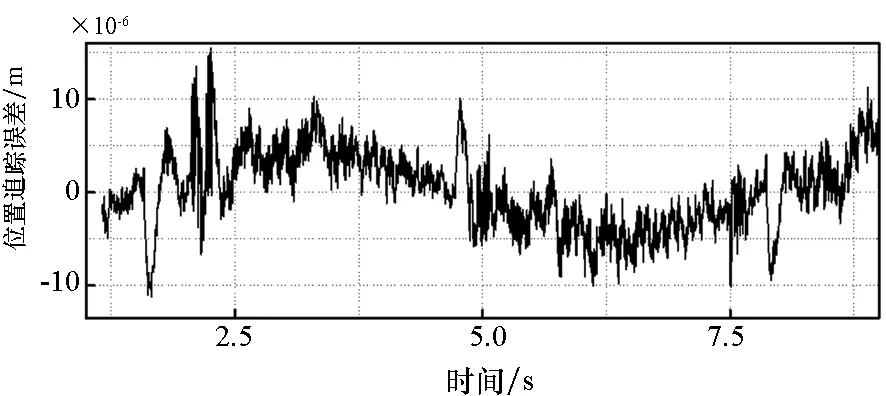
图9 补偿后位置追踪误差的局部放大图Fig.9 Local large map of position tracking error after compensation

6 结论

在分析LESO观测原理的基础上，通过对误差系统的线性近似，推导出状态观测静差的量化表达式，进而据此设计了误差前馈补偿器。通过理论推导，证明了补偿的可行性——在时域内能消除观测静差，频域上也能够减轻LESO的相位滞后，进而将这种补偿思想引入NESO中。仿真验证了补偿器对LESO、NESO均有效，实验结果则进一步表明，补偿器的引入能大幅提高整个LADRC系统的控制精度。

这种补偿器的设计源自观测静差表达式的推导，形式简单，没有积分、微分等环节，计算量小； ESO与补偿器一一对应，不存在多样性；以串联的形式引入ADRC中，与其他环节相互独立，且对LESO、NESO均有效；在观测足够迅速的前提下，理论上能完全消除观测静差，显著提高系统的控制精度。该前馈观测补偿设计可为实际工程应用提供思路参考。