基于前景理论和证据推理的混合型多属性决策方法*
2019-10-14罗承昆陈云翔顾天一项华春
罗承昆,陈云翔,顾天一,项华春
(1. 空军工程大学 装备管理与无人机工程学院, 陕西 西安 710051; 2. 中国人民解放军66139部队, 北京 100041)
多属性决策方法在社会、经济和军事等诸多领域得到了广泛的应用。由于决策环境的复杂性,决策过程中的属性评估参数往往包含不精确、不完整、甚至完全未知的信息,仅仅用精确数难以表达,应该结合区间数、模糊数和语言变量等形式进行刻画。因此,针对混合型多属性决策问题开展研究具有重要的理论和实践价值。
现有的混合型多属性决策方法大多是根据期望效用理论提出的,即完全掌握相关决策信息,追求效用最大化。但在实际决策过程中,决策者通常会表现出有限理性的心理特征(比如参考依赖、对损失和收益的风险偏好不同等),基于期望效用理论的决策方法难以反映决策者的真实选择。随着行为决策理论的发展,基于有限理性假设的前景理论[1-2]以其符合决策者思维习惯的优势得到了越来越多的关注。文献[3]采用三角模糊数对混合型信息进行统一,结合前景理论提出了一种基于改进投影理论的风险型群决策方法。文献[4]针对以区间数、三角模糊数和梯形模糊数表示的风险型混合多属性群决策问题,提出了一种基于前景理论的决策方法。
上述研究有力地推动了基于前景理论的混合型多属性决策方法的发展,但是其采用加权和法对不确定信息进行融合,往往容易造成信息丢失。更有效的方法是将收集到的定性知识与定量信息看作是判断和推理的证据,采用证据推理算法融合决策信息,并对方案进行评估和排序。文献[5]根据直觉模糊数对混合型信息进行统一,提出了一种基于前景理论和证据推理的决策方法,但在融合信息前采用主观估计法直接获得属性权重,决策结果的可信度较低。在文献[5]的基础上,文献[6]基于直觉模糊熵和交叉熵建立了属性权重确定模型,进而提出了权重不确定条件下的决策方法,但在计算属性权重的过程中难以合理确定偏好因子参数,并且属性权重计算量较大。针对以上问题,本文提出一种基于前景理论和证据推理的混合型多属性决策方法。
1 预备知识
1.1 直觉模糊集
相比于模糊集,直觉模糊集同时考虑了隶属度和非隶属度两方面的信息,能够更好地表达和处理事物属性中的模糊性与不确定性,因此自提出以来得到了广泛的研究与应用。
定义1[7]设X为一个给定的论域,则称B={〈x,μB(x),vB(x)〉|x∈X}为X上的一个直觉模糊集。其中,μB(x)和vB(x)分别为X中元素x属于B的隶属度和非隶属度,μB:X→[0,1],vB:X→[0,1],且0≤μB(x)+vB(x)≤1,∀x∈X。X中元素x属于B的犹豫度为πB(x)=1-μB(x)-vB(x)。μB(x)和vB(x)组成的有序对(μB(x),vB(x))称为直觉模糊数。
定义2[7]设b=(μb,vb)、b1=(μ1,v1)和b2=(μ2,v2)为直觉模糊数,λ为任意实数,则直觉模糊数的运算法则为:
4)b1⊕b2=(μ1+μ2-μ1μ2,v1v2)。
定义3[7]设有直觉模糊数b=(μb,vb),定义S(b)=μb-vb为b的记分函数,H(b)=μb+vb为b的精确函数。对于直觉模糊数b1=(μ1,v1)和b2=(μ2,v2),可根据其记分函数和精确函数比较它们的大小:
1)若S(b1)>S(b2)或S(b1)=S(b2)∧H(b1)>H(b2),则b1>b2;
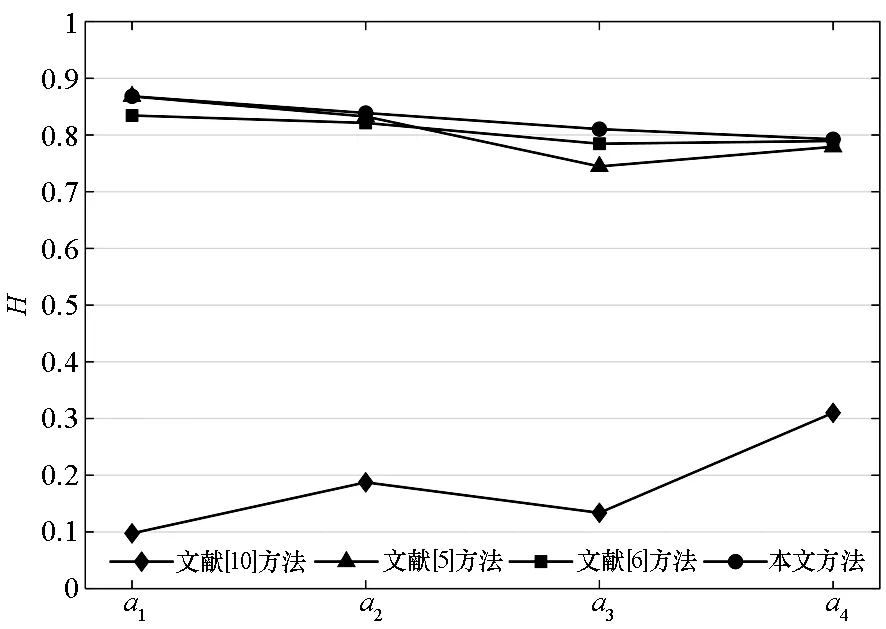
2)若S(b1) 3)若S(b1)=S(b2)∧H(b1)=H(b2),则b1=b2。 前景理论考虑了不确定环境下决策者的心理行为特征,认为决策者在决策过程中并不是追求效用最大的目标,而是选择综合价值最满意的决策方案。价值函数[1]是前景理论的重要组成部分,其计算公式为 (1) 其中:x≥0为收益,x<0为损失;α与δ代表风险态度系数,0≤α≤1,0≤δ≤1;σ代表损失规避系数,σ>1。 基于Dempster组合规则,Yang等[8]提出了递归形式的证据推理算法,为解决不确定决策问题提供了一种非线性多源信息融合方法。针对递归算法计算复杂度较高的问题,文献[9]在递归算法的基础上进一步提出了解析形式的证据推理算法。 设N个相互独立的评价等级构成辨识框架Θ={θp|p=1,2,…,N},则证据eq(q=1,2,…,Q)的评价结果可用置信结构表示为 T(eq)={(θp,βp,q);(Θ,βΘ,q)} (2) (3) 式中:mp,q为证据eq被评为等级θp的基本概率分配;P(Θ)为Θ的幂集,mP(Θ),q为证据eq未被评为任何等级的基本概率分配。 将Q个证据的基本概率分配进行合成,得到综合评价结果为 (5) (6) (7) (8) (9) 其中:φ为归一化因子,反映各证据之间的冲突程度;βp为等级θp的置信度;βΘ为未被评为任何等级的置信度。 针对属性值以精确数、区间数和语言变量等形式表示的决策问题,首先需要根据直觉模糊数对混合型信息进行统一。 (10) (11) (12) 其中:fij与oj的大小关系可通过定义3进行判断;DIFS(fij,oj)表示fij与oj之间的直觉模糊距离[10],其计算公式为 DIFS(fij,oj)=(1-max(U(fij,oj),V(fij,oj)), min(U(fij,oj),V(fij,oj))) (13) 属性的可靠性反映的是属性关于方案集的评价信息的可靠程度,具有绝对性和客观性;属性的重要性反映的是不同属性对决策结果的影响程度,具有相对性和主观性。在解决多属性决策问题时,为确保决策结果科学合理,通常应该同时考虑属性的可靠性与重要性,进而确定属性权重。 2.3.1 基于直觉模糊熵与相似度的属性可靠性评估 当前,常用的属性可靠性评估方法大都是基于直觉模糊熵来评估属性可靠性[11],即根据各属性关于方案集的评价信息的不确定度来确定属性的可靠度。事实上,直觉模糊熵只是衡量属性可靠度的关键因素之一,它是从属性评价信息的自身清晰程度反映属性的可靠性。相似度作为反映各属性评价信息之间相似关系的重要指标,从属性的外部关系反映了属性的可靠性,是衡量属性可靠度的另一个重要因素[12]。为了对属性的可靠性进行全面客观的评估,提出一种基于直觉模糊熵与相似度的属性可靠性评估方法。 直觉模糊熵自1996年由Burillo等[13]提出以来,其公理化定义和公式构造形式得到了不断的改进和完善。文献[14]在分析现有直觉模糊熵的定义和公式可能存在失效问题等不足的基础上,提出了新的直觉模糊熵及相似度度量方法,并通过算例对比验证了其合理性和有效性。 定义4[14]设B={〈xk,μB(xk),vB(xk)〉|xk∈X}和M={〈xk,μM(xk),vM(xk)〉|xk∈X}为论域X={xk|k=1,2,…,K}上的任意直觉模糊集,则B的直觉模糊熵为 (14) B与M的直觉模糊相似度为 S(B,M)= (15) 在决策过程中,某属性关于方案集的前景决策信息的不确定度越小,那么决策信息越有用,该属性的可靠度越高。 属性cj关于方案集的前景决策信息的不确定度为 (16) 确定属性可靠度时,除了要考虑属性关于方案集的前景决策信息自身的不确定性,还要考虑属性与其他属性决策信息的相似性。 属性cj关于方案集的前景决策信息与其他属性的前景决策信息之间的相似度为 (17) Sj越大,属性cj关于方案集的前景决策信息与其他属性的前景决策信息越一致,其可靠度越高;反之,可靠度越低。 因此,Ej与Sj度量了决策信息的不确定性与相似性,在计算属性可靠度时应综合进行考量。 融合Ej与Sj,得到属性cj的定权函数为 Yj=(1-Ej)+Sj (18) Yj越大,说明属性cj越可靠。 因此,得到属性cj的可靠度为 (19) 2.3.2 基于可靠度与重要度的属性权重确定 现有的属性权重确定方法大都只考虑了属性的可靠性或重要性中的一个因素,实际上这两个因素对决策结果均有较大影响。 只有当某个属性既可靠又重要时,才能赋予其较大的权重。 因此,在分别确定可靠度与重要度的基础上,得到属性cj的权重为 (20) 对wj进行归一化处理,最终得到属性cj的权重为 (21) 将属性cj关于方案ai的直觉模糊前景价值zij看作一条证据,采用证据推理算法集结所有属性的直觉模糊前景价值,即可确定方案ai的综合前景值。 对于前景决策矩阵Z=[zij]m×n,设前景等级集合[5]为Θ={θh|h=1,2}。其中,θ1=(μz,vz)=(1,0)表示完全达到了预期,θ2=(μz,vz)=(0,1)表示完全没有达到预期。那么zij可表示为 T(cj(ai))={(θh,βh,ij),h=1,2;(Θ,βΘ,ij)} (22) 令mh,ij表示属性cj对方案ai在等级θh下的基本概率分配,mP(Θ),ij表示属性cj对方案ai未被评为任何等级的基本概率分配,则有 (23) 将所有属性对方案ai的基本概率分配进行合成,有 (24) (25) (26) (27) 那么,方案ai的综合评价结果为T(ai)={(θh,βh,i),h=1,2;(Θ,βΘ,i)}。其中 (28) (29) 通过上述分析,本文方法的决策流程为: 步骤1:运用式(10)~(11)将混合型决策矩阵D=[dij]m×n统一为直觉模糊决策矩阵F=[fij]m×n。 步骤2:确定参考点向量O=[oj]1×n,通过式(12)~(13)计算得到前景决策矩阵Z=[zij]m×n。 步骤4:根据证据推理算法,运用式(22)~(29)集结属性权重和前景决策矩阵,得到各方案的综合前景值Z(ai)。 步骤5:根据定义3比较综合前景值Z(ai)的大小,最终确定方案排序。 为验证本文方法的性能,本节运用文献[5]的算例数据进行计算,并与文献[5]方法、文献[6]方法、文献[10]方法进行对比分析。 对于某航运企业竞争力评估问题,假设有4家班轮公司ai(i=1,2,3,4),5个属性分别为净资产收益率(c1)、资产负债率(c2)、船队规模(c3)、组织结构与战略和环境的匹配度(c4)、安全性(c5)。其中,c1和c2为精确数,c3为区间数,c4和c5为语言变量,除c2为成本型外,其他为效益型。属性权重完全未知且为实数,目标向量为G=[5,55,[500 000,700 000],[平均,高],[平均,高]],初始决策矩阵如表1所示。 表1初始决策矩阵 Tab.1 Initial decision-making matrix c1/%c2/%c3/TEUc4c5a13.0363.08[464 986,825 454][平均,很高][很低,高]a23.9866.61[534 211,975 426][低,高][低,最高]a35.8451.89[340 131,555 525][很低,高][平均,很高]a44.2853.54[465 228,693 691][低,平均][低,高] 运用本文方法对4家班轮公司进行评估和排序,具体步骤如下: 步骤1:目标向量与初始决策矩阵构成决策增广矩阵Do=[dsj]5×5,通过混合型信息的统一得到直觉模糊决策增广矩阵F=[fij]4×5和参考点向量O=[oj]1×5: 步骤2:根据Tversky[2]的实验数据,考虑α=δ=0.88,σ=2.25,通过式(12)~(13)计算得到前景决策矩阵Z=[zij]4×5: 步骤4:根据证据推理算法,运用式(22)~(29)集结属性权重和前景决策矩阵,得到各班轮公司的综合前景值Z(ai): Z(a1)=(0.073 0,0.795 3) Z(a2)=(0.157 0,0.681 8) Z(a3)=(0.118 1,0.692 3) Z(a4)=(0.290 5,0.502 1) 步骤5:根据定义3得到各班轮公司的记分函数值为S(a1)=-0.722 3,S(a2)=-0.524 8,S(a3)=-0.574 2,S(a4)=-0.211 6;精确函数值为H(a1)=0.868 3,H(a2)=0.838 8,H(a3)=0.810 4,H(a4)=0.792 6。因此,各班轮公司的排序结果为a4≻a2≻a3≻a1。 为进一步验证本文方法的性能,分别运用文献[6]方法和文献[10]中的直觉模糊加权平均(Intuitionistic Fuzzy Weighted Averaging, IFWA)算子对上述前景决策矩阵进行合成,确定各班轮公司的排序结果,并与文献[5]方法、本文方法进行对比分析。运用以上4种方法得到的决策结果如表2所示。 由表2可知,4种方法得到的排序结果相同,从而验证了本文方法具有可行性和有效性。为进一步与文献[5]方法、文献[6]方法、文献[10]方法开展比较,图1~2分别给出了基于记分函数和精确函数的决策结果对比情况。通过对图1~2进行分析可以发现,文献[5]方法得到的精确函数值明显高于文献[10]方法,说明采用证据推理算法进行属性信息集结,能够最大限度地减少信息丢失,降低决策结果的不确定性。相比于文献[5]方法、文献[6]方法,本文方法在确定属性权重时不仅考虑了属性的重要性,还根据决策信息的不确定度与相似度考虑了属性的可靠性,属性权重确定结果更加全面合理,因而得到的记分函数值之间区分度更大,精确函数值更高,更有利于做出决策。因此,本文方法与其他3种方法相比更具优越性。 图1 基于记分函数的决策结果对比Fig.1 Comparison of decision-making results based on score function 表2 4种方法得到的决策结果 图2 基于精确函数的决策结果对比Fig.2 Comparison of decision-making results based on accuracy function 针对属性权重完全未知的混合型多属性决策问题,提出了基于前景理论和证据推理的决策方法。考虑了决策信息的不确定性与相似性,从直觉模糊熵与相似度两个方面提出了属性可靠性评估方法,进而结合属性重要度确定了属性权重,确保了属性权重的全面性与合理性。算例分析结果表明,本文方法得到的决策结果更具有区分度、不确定性更低,适合用来处理混合型多属性决策问题。1.2 前景理论
1.3 证据推理
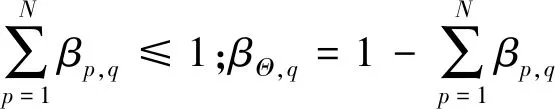
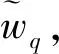
2 混合型多属性决策模型
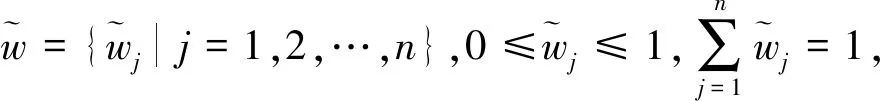
2.1 基于直觉模糊数的混合型信息统一
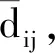
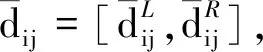
2.2 基于前景理论的决策信息转化
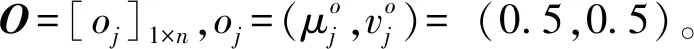
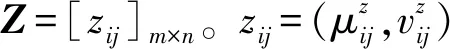
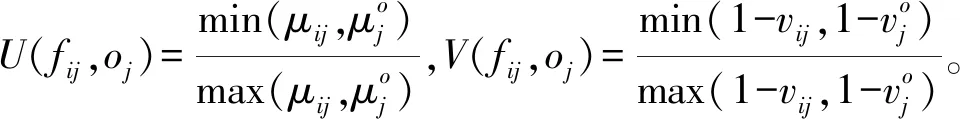
2.3 考虑可靠性与重要性的属性权重确定
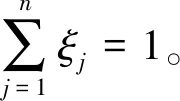
2.4 基于证据推理的属性信息集结
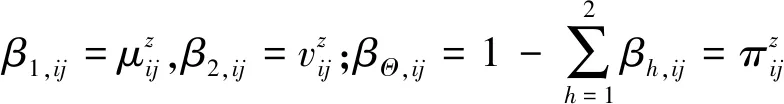

3 算例分析
3.1 问题描述
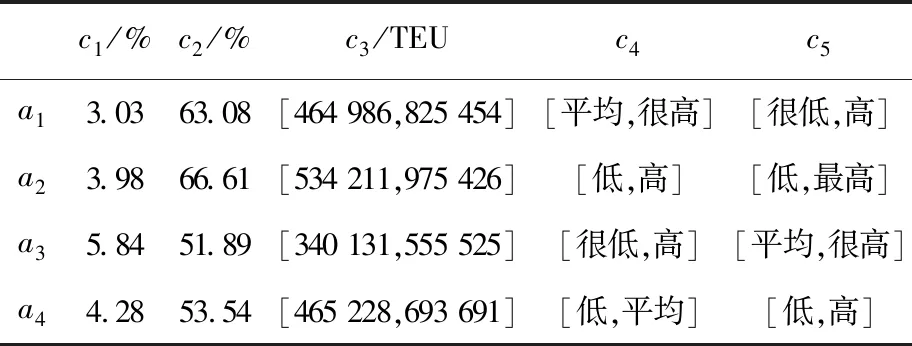
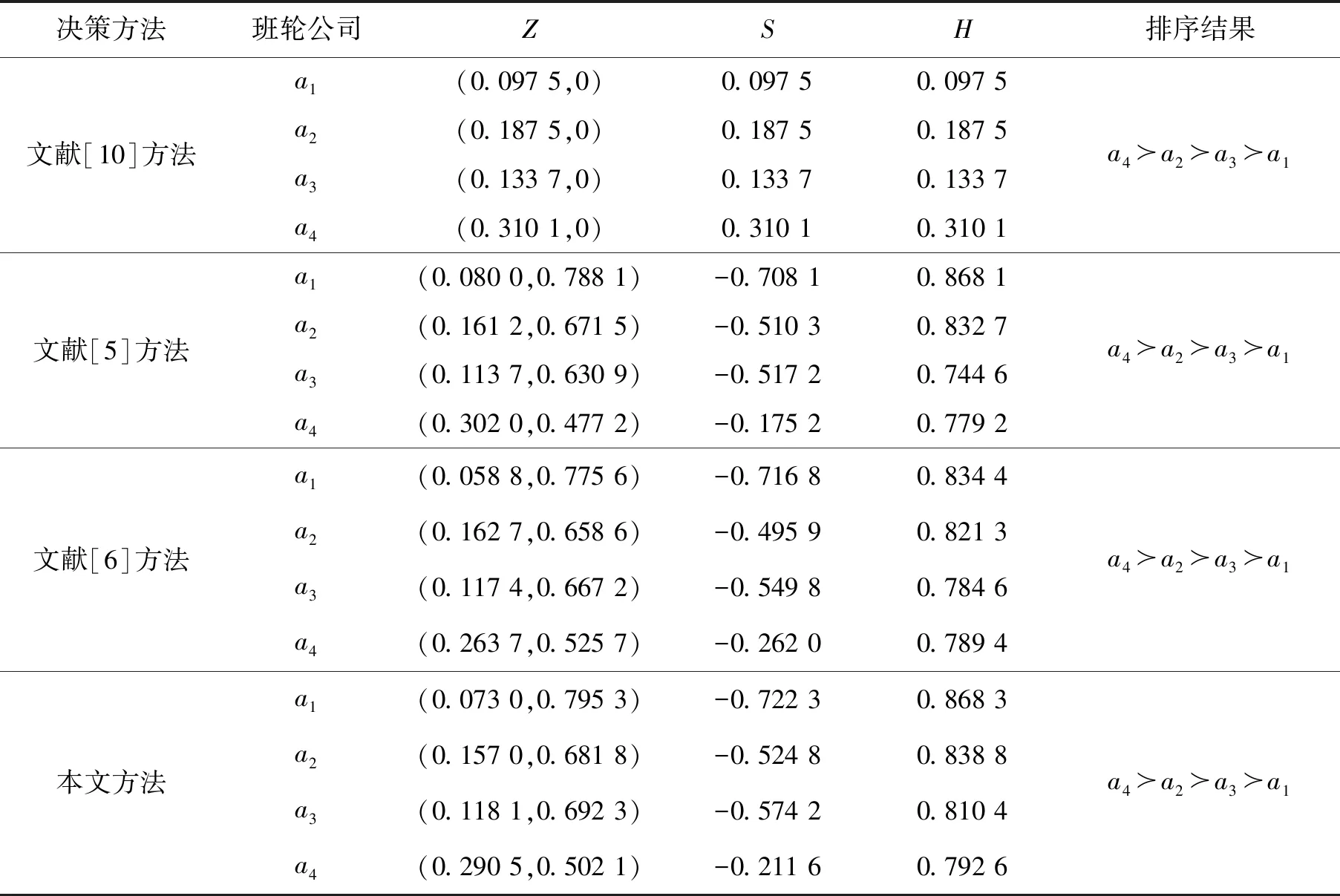
3.2 决策过程

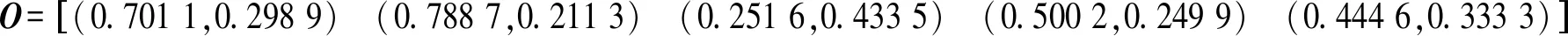

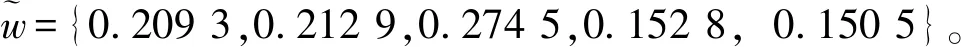
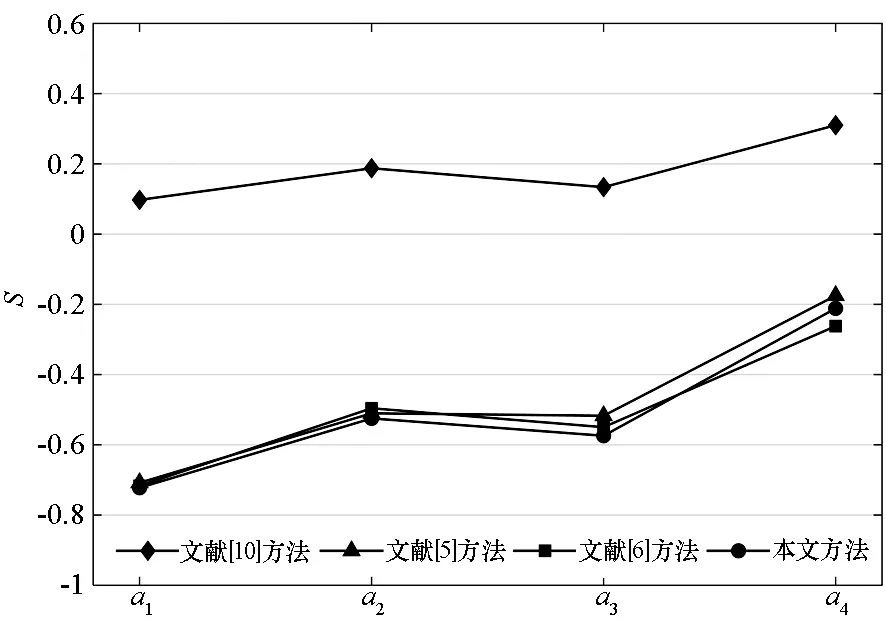
3.3 对比分析
4 结论
