适用于北斗混合星座的相对定位随机模型建模策略*

伍劭实，赵修斌，庞春雷，张 良，刘亚东

(1. 空军工程大学 信息与导航学院， 陕西 西安 710077； 2. 中国人民解放军95853部队， 北京 100076)

精确建立随机模型是全球导航卫星系统(Global Navigation Satellite System, GNSS)精密测量与定位的先决条件[1]，其在精密相对定位中通常具有两个方面重要作用：一是提高模糊度浮点解的精度，进而提高模糊度固定成功率，提高相对定位的可靠性；二是提高基线解的精度[2-3]。当前，国内外学者对随机建模进行了广泛而深入的研究，主要集中在基于仰角和基于载噪比的模型[4-5]。文献[6]提出了卫星仰角模型，认为GPS卫星观测量噪声与卫星仰角相关，随后，文献[7-10]在此基础上引入了观测量相关性和时间相关性，使得根据GPS卫星仰角建立的随机模型更加准确。载噪比模型最先在文献[11]中被提出。基于此，文献[12-13]分别提出了Sigma-ε模型和Sigma-Δ模型，前者提高了低仰角GPS卫星的定位精度，后者在此基础上考虑了GPS卫星信号通过障碍物发生衍射带来的定位误差影响。文献[14]进一步考虑了空间物理相关性，并由此提出了sigma-C模型，使得此类基于载噪比的模型更加准确。由此可以看出，关于随机模型的研究主要是针对GPS展开，对于北斗的随机模型研究还相对较少的。当前，我国自主建设发展的北斗卫星导航系统正在向第三代全球导航系统过渡，针对北斗的随机模型研究也逐渐增多。为准确合理地确定观测量随机模型，国内外学者提出了许多行之有效的方差分量估计方法，如Helmert方差分量估计、最小范数二次无偏估计、最优不变二次无偏估计、最小二乘方差分量估计(Least-Squares Variance Component Estimation, LS-VCE)等。其中LS-VCE基于最小二乘准则，具有简单、灵活等优点[15]。文献[3]采用LS-VCE，针对北斗三频信号的随机特性进行了系统深入的研究，发现采用仰角模型时，地球静止轨道(Geostationary Earth Orbit, GEO)卫星的拟合误差要大于倾斜地球同步轨道(Inclined Geosynchronous Satellite Orbit, IGSO)和中地球轨道(Medium Earth Orbit, MEO)卫星。

当前，北斗随机模型的研究主要借鉴了GPS的方法，然而北斗和GPS具有诸多不同，特别是在卫星轨道设计上，北斗由三轨道星座混合而成，不同轨道卫星的观测噪声具有明显差异[4，16]。因此，针对单一星座的GPS采用的单一卫星仰角或载噪比模型，可能无法很好地适用于北斗系统。基于此，提出了一种适用于北斗的随机模型建模策略，即混合随机建模。

1 单差模型及残差

为了得到不同轨道卫星的测量噪声特性，需利用单差模型计算残差。假设基准站接收机r和移动站接收机m同时观测n颗卫星，则短基线单频单历元单差相对定位模型为：

(1)

δt′=δt+λa1

(2)

则式(1)可写为：

(3)

利用双差模型，可提前准确确定双差模糊度和基线向量b，则式(3)中仅剩下钟差项δt′和dt，并可被精确估计，由此可得单差观测量残差为：

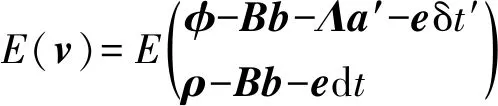
(4)

2 LS-VCE观测量方差-协方差阵

确定观测量方差-协方差阵未知分量的过程即为方差分量估计[3]。采用LS-VCE进行观测量的方差-协方差阵估计。

假设线性观测模型为：

(5)

其中：y为观测向量；A为列满秩系数矩阵；x为待估参量；Qyy为观测量y的方差-协方差阵；Qk为协因数阵，其中k=1，2，… ，p；Q0为Qyy中已知的部分；σk为方差分量；E[ ]和D[ ]分别为期望和方差算子。

由文献[15]可知，方差分量的最小二乘解为：

(6)

(7)

(8)

式(7)和式(8)可用来有效估计观测量的协方差阵，但由此会带来可估性的问题，即Qyy无法通过式(7)和式(8)一次性获得，需要进行迭代估计[3]。本文采用一种简化的LS-VCE方法估计观测量的协方差阵。由文献[15]可知，若y为0均值随机向量，则其方差-协方差阵为：

(9)

结合式(4)，在各参量都被精确估计的前提下，若单差观测量残差满足0均值随机分布的条件，则可通过残差的协方差阵来近似得到单差观测量的协方差阵。以某一天24 h北斗实测B1观测量单差残差直方图为例，如图1所示，北斗观测量单差残差近似满足0均值正态分布，因此可通过式(9)近似估计单差观测值得协方差阵，将其作为观测模型的随机模型。

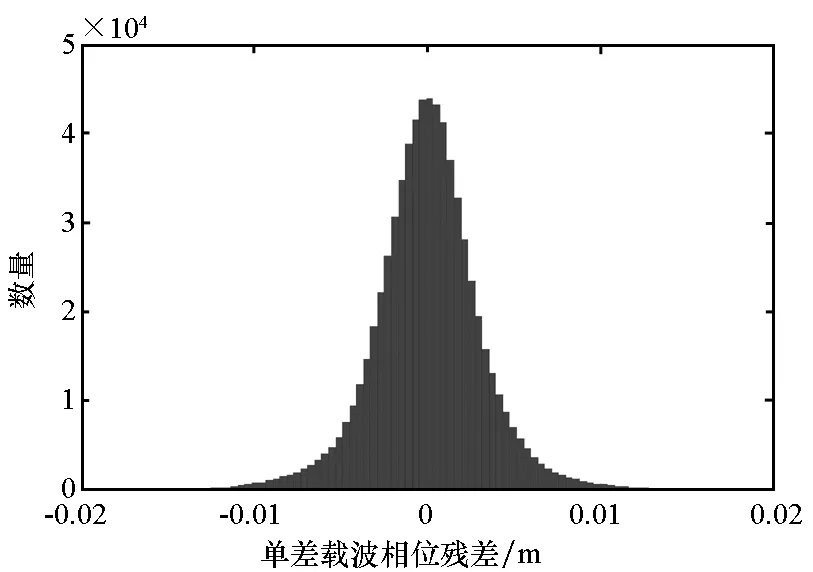
(a) 单差载波相位观测量残差直方图(a) Histogram of single-differencing phase observation residuals

(b) 单差伪距观测量残差直方图(b) Histogram of single-differencing code observation residuals图1 北斗B1频点观测量残差直方图Fig.1 Histogram of observation residuals on BDS B1

3 构建随机模型

通过式(4)和式(9)估计得到单差观测量的协方差阵后，即可利用特定模型对其进行拟合。当前常用的模型为卫星仰角模型和载噪比模型。

3.1 卫星仰角模型

卫星仰角模型反映了卫星观测量标准差与卫星仰角的关系，常用的是指数模型[6]和三角函数模型[17]，分别表示为：

σ=a1+a2·e-θ/θ0

(10)

(11)

其中：σ表示单差观测量标准差，当表示相位观测量标准差时单位为mm，当表示伪距观测量标准差时单位为m；a1和a2为需要拟合的模型参数；θ为卫星仰角；θ0为仰角误差标度值[6]。根据式(10)或式(11)可以建立双差观测模型的随机模型：

(12)

3.2 载噪比模型

载噪比模型反映了卫星观测量标准差与卫星信号载噪比的关系，其表达式[11]为：

(13)

式中：σ2为非差观测量方差，m2；b1为需要拟合的模型参数；C/N为所接收卫星信号的载噪比。

根据式(13)可以建立双差观测模型的随机模型：

(14)

基于仰角或载噪比的模型在GPS随机模型研究中发挥了重要作用，也取得了不少研究成果。然而与单一星座的GPS不同，北斗由三轨道星座混合而成，因此在建立随机模型的过程中，不能完全照搬GPS中的方法，而是应该寻找适合于北斗特点的随机建模方法。

4 试验结果与分析

4.1 试验条件

采用一对接收机和一对天线，两天线固定于楼顶，基线长为2.17 m，数据长度为13.5 h，采样率为1 Hz，卫星截止角设为15°。试验前先利用长期观测数据拟合混合模型的各个参数，如表1所示。然后根据混合模型确定观测模量随机模型，对采集的北斗静态数据进行逐历元相对定位解算。尽管采用多频或多系统能显著提高模糊度解算效果[18-19]，但考虑到单频单历元是最为苛刻的条件，因而在单频单历元条件下验证所提混合模型的性能，试验中B1和B2频点所用卫星一致。

表1 混合模型参数

由于采用单历元解算，因此未考虑观测量的时间相关性。试验中所用四种随机模型分别为简化等权随机模型(假设同一频率上不同卫星的相位或伪距测量标准差为常量，取最小测量单元的1%作为观测量标准差，例如对于B1载波相位，观测量标准差为1.92 mm，模型一)、单一仰角模型(模型二)、单一载噪比模型(模型三)和所提混合模型(新模型)。

4.2 试验过程与分析

图2以B1频点为例，给出了简化等权模型和新模型情况下三颗代表不同类型的卫星(PRN4(GEO)、PRN9(IGSO)、PRN14(MEO))相位和伪距单差残差对比结果。由图2可知，新模型能在一定程度上抑制观测量的噪声，因而有利于双差模糊度的解算及基线解精度的提高。

为统计模糊度成功率，首先利用静态基线向量这一已知条件，确定B1和B2单频双差模糊度，将其作为参考值。然后分别利用四种随机模型，解算可视卫星数分别为5(1IGSO+4GEO)、6(1IGSO+5GEO)、7(1MEO+1IGSO+5GEO或2IGSO+5GEO)、8(1MEO+2IGSO+5GEO或3IGSO+5GEO)情况下的B1和B2单频双差模糊度，将其与提前确定的模糊度参考值进行比较，计算以上不同情况下的单频双差模糊度成功率(模糊度正确固定历元数与总历元数之比)，结果如表2所示。由表2可知，除了B2频率5颗卫星情况下所提混合模型模糊度成功率略低于模型二(单一仰角模型)，其余情况下所提模型的模糊度成功率均最高；尽管随着卫星数的增加，四种模型下的模糊度成功率均大幅提升，但模型一(简化等权模型)相比于其他三个模型的提升幅度最小，尤其是7颗星的情况，此时模型一的模糊度成功率低于27%，而其他三种模型下成功率已达到85%以上，说明随机建模与否对于模糊度解算的影响不容忽视。

(a) 相位单差残差(a) Phase single residuals

(b) 伪距单差残差(b) Pseudo-distance single difference residuals图2 不同类型的北斗卫星利用简化模型和新模型得到的B1单差残差Fig.2 Single-difference residual of different BDS satellites on B1 with the simplified and the new stochastic model

接下来统计模糊度正确固定的前提下可视卫星数分别为5、6、7、8时，采用四种模型计算得到的基线解精度，结果如图3和图4所示。由图3和图4可知，采用后三个随机模型所得基线解精度相差不大，但相比于模型一精度更高。尽管在基线解精度方面新模型性能并非最优，甚至有时略低于模型二和模型三(比如B2的7颗星情况)，但其仍然保持着较好特性，同时结合表2中模糊度成功率结果，说明新模型的综合性能最优。

表2 四种模型下得到的单频双差模糊度解算成功率

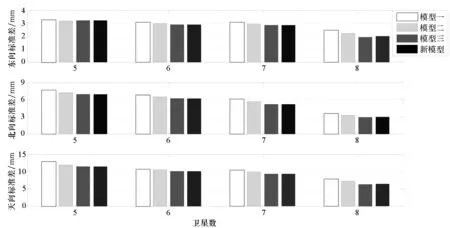
图3 B1频率上基线分量标准差Fig.3 Standard deviations of baseline components on B1

图4 B2频率上基线分量标准差Fig.4 Standard deviations of baseline components on B2

5 结论

与传统采用单一模型建立随机模型的方法不同，混合建模策略针对不同轨道的北斗卫星分别建立随机模型：对于GEO卫星，采用载噪比模型；对于IGSO和MEO卫星，均采用仰角模型。实测数据结果表明；采用所提混合模型，模糊度解算成功率最高，同时在基线解精度上也具有较好特性，综合性能最优。因而相比于传统简化模型和单一的仰角或载噪比模型，混合模型更适用于北斗系统。