基于遥感图像及工程参数的全局像移探测算法
2019-10-14刘海秋高彦伟闫得杰
刘海秋,高彦伟,闫得杰
(1.安徽农业大学 信息与计算机学院,安徽 合肥 2300362.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)
引言
像移作为影响空间相机成像质量的关键因素之一,描述了空间相机在轨运行期间由轨道运动、地球自转、飞行器姿态变化、活动部件运动等因素导致的目标景物在焦面上映射的像与焦面之间的相对运动[1-2]。随着空间相机地面分辨率不断提高,像移对像质的影响日益严重,如何准确地获取像移,是实现像移补偿,进而削弱像移对像质影响的前提[3-6]。国内外相关学者提出了多种像移获取方法,可以归纳为3类。
第1类,基于工程参数的像移计算方法。由于像点与物点的三维坐标之间存在一定的几何关系,通过建立两者之间的坐标变换公式,并根据物点的地理位置坐标,以及星下点经纬度、轨道高度、飞行器三轴姿态角及角速度等数据(统称为工程参数),计算像点在焦面上的位置坐标。Miller.B.M等人建立了简单的坐标变换模型[1],为进一步提高模型的准确度,长春光机所王家骐院士利用齐次坐标变换方法,提出了精确的对地探测坐标变换公式[7],目前我国包括XX-1号空间光学遥感器在内的多台相机都采用该方法探测像移。然而,在轨运行结果表明,该方法的像移测量带宽不仅受限于各种工程参数测量装置的带宽,也受限于飞行器对工程参数的更新周期,虽然在1 Hz以下的低频像移计算方面取得了理想效果,但是难以成为高频像移探测的有效手段。
第2类,基于联合相关器的像移估计方法。通过在焦面上增加辅助的面阵成像传感器,获得具有重叠区域的图像序列,利用光学透镜组成联合变换器,对图像序列做相关运算得到匹配误差,将该匹配误差近似为像移[8]。K.Janschek等人提出这种方法,并巧妙地运用光学联合变换器对图像进行快速匹配处理,解决了当时电子学处理器速度低、实时性差的问题[9]。戴朝约等人分别通过改进PA算法、双三次样条插值、双相位编码等方式,提高像移测量的准确度[10]。此外,樊超等人分析了目标景物、像移大小、窗口尺寸对像移测量精度的影响,验证了该方法的有效性[11]。该方法的测量位置在焦面处,更能反映焦面像移的真实状态,增加的面阵成像传感器能够进行高帧频拍摄,可以达到较高的像移测量带宽。但是,在低轨高速运行环境中,面阵成像传感器信噪比低,像移测量精度难以保障[12],该方法在低轨高分辨率空间相机上的应用前景有限。
第3类,基于遥感图像的像移测量方法。利用焦面上平行排布的成像传感器拍摄得到平行观测图像,通过配准技术得到配准误差序列,采用频谱分析技术,提取配准误差频谱曲线中峰值点的频率、幅值和初相位信息,进而求取像移峰值点处的频率、幅值和初相位,并以三角函数的形式拟合像移。Akira Iwasaki等人运用ASTER相机多谱段图像探测到了1.5 Hz处的像移[13]。Sarah S. Mattson等人利用LROC-NAC相机图像探测到6 Hz处的像移[14],并采用HiRISE相机中红光波段图像捕捉到2 Hz处的像移[15]。孙涛等人采用MS-1卫星遥感图像检测到0.1 Hz和0.6 Hz的像移[16]。童小华和王密等人发现在资源三号卫星上存在0.6 Hz左右的像移[17-18]。
基于遥感图像的像移测量方法选取焦面上主成像传感器所成图像为数据源,测量结果能够反映成像时刻和成像位置处像移的真实状态,且像移测量效果不受限于惯性测量设备,人们关注的焦点逐渐从依赖于惯性测量设备的低频像移测量,过渡到从遥感图像中挖掘高频像移信息的阶段,各国学者纷纷利用遥感图像尝试对本国卫星的像移进行探测。值得注意的是,相邻两片成像传感器的拼接区能够对同一目标景物先后成像2次,从而形成具有相同目标景物的图像,是该方法获取像移信息的关键[12-18]。然而,对于推扫式空间相机而言,具有相同目标景物的视差图像并非贯穿每次成像任务,在成像初始阶段,相邻两片成像传感器拼接区的投影范围不重合,输出的遥感图像中无相同目标景物,虽然无相同目标景物期间所占时间较短,但位于每次成像的初始阶段,该阶段像移的准确估计,是成像初期在轨实时像移补偿的基本依据,而成像初期的像移补偿效果直接影响整个拍摄阶段的成像质量,因此,无相同目标景物期间像移的准确估计至关重要。由于此期间所成的遥感图像中无相同目标景物,单纯地依赖遥感图像并不能成功地反演像移信息,本文提出基于遥感图像和工程参数的全局像移探测算法,对无相同目标景物和有相同目标景物期间的像移进行全覆盖估计。
1 无相同景物期间的像移估计
1.1 TDICCD拼接区的成像特点
空间相机焦面上通常存在多片CCD,并以如图1所示的交错拼接方式进行排布。在相邻两片CCD的拼接区往往存在数十列重叠像元[19-21],正射成像时拼接区在地球表面的投影区域相互重合,重合范围内的目标景物会被两片CCD的拼接区先后分时拍摄2次。假设2次成像的时间差为δ,一次成像过程的起止时刻分别为0和Ts,则在区间[δ,Ts-δ]内,地球表面的目标景物会被1#CCD和2#CCD先后成像2次,形成具有相同目标景物的视差图像。然而,在区间[0,δ]内,1#CCD的拍摄范围Region1不会被2#CCD捕捉到,同理,在区间[Ts-δ,Ts]内,2#CCD的拍摄范围Region2也不会被1#CCD捕捉到。因此,在每次成像任务的最初和最后δ期间,相邻两片CCD拼接区视差图像中无相同的目标景物,但最后δ期间的无相同景物区域对像移估计并不重要。
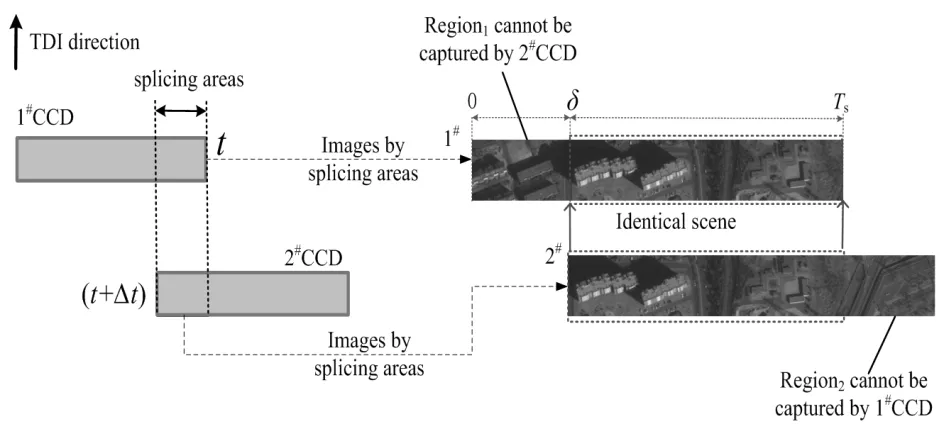
图1 CCD拼接区的成像特点Fig.1 Imaging characteristics of CCD slicing areas
虽然在一次拍摄任务中,无相同目标景物期间所占比例较少,以本文实验所采用的XX-1号空间光学遥感器为例,无相同目标景物期间的持续时间约为226 ms,仅占一次拍摄时长的0.8%(由中科院长春光机所提供),但是,无相同目标景物期间处于每次拍摄任务的起始阶段,起始阶段的像移准确估计,是拍摄初期在轨实时像移补偿的基本依据,而拍摄初期的像移补偿效果直接影响整个拍摄任务阶段的成像质量,因此,无相同目标景物期间像移的准确估计至关重要。
1.2 无相同景物期间的像移获取
作为像移的形成因素之一,活动部件振动的带宽可以高达几百赫兹,由此引起的像移带宽较宽,尽管如此,但是随着频率的增加,像移的功率谱密度往往呈现下降的趋势[22],像移的绝大部分能量集中在低频段[23]。此外,对于CCD所成图像而言,相邻两行图像之间的时间差与CCD的像元尺寸和飞行器所处的轨道高度等参数有关,一般情况下,高分辨率空间相机的行扫描频率可以达到上万赫兹[24]。相机的逐行扫描过程可以看作对像移的实时采样,在上万赫兹的采样频率下,高频像移能够被记录在CCD拼接区所成的两幅视差图像中,并以相同目标景物在两幅图像中的位置偏移量的形式展现出来。基于上述原理,该部分采用空间相机在轨运行期间实时采集的工程参数,提取低频的像移信息,并利用具有相同目标景物的视差图像获取位置偏移量数据,构建基于拼接区图像和低频分量的目标函数,用以衡量像移曲线与低频像移之间的偏差程度,筛选无相同目标景物期间像移的最优估计,如图2所示。
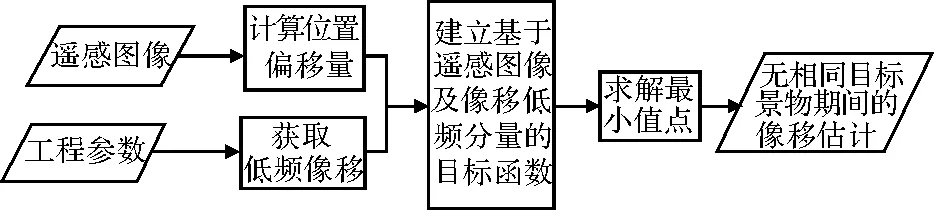
图2 无相同目标景物期间的像移估计方案Fig.2 Image motion estimation scheme during period without identical scenes
1.2.1 利用图像配准方法获取视差图像中位置偏移量
像移描述了像点与焦面之间的相对运动,由于相邻两片CCD的拼接区对同一目标景物的成像时刻不同,而不同时刻像移的取值和方向[25]可能导致同一目标景物在拼接区所成的两幅视差图像中的位置存在偏差。位置偏移量描述了相同目标景物在两幅视差图像中的位置偏差程度,在利用图像配准方法确定位置偏移量之前,需要提取一次拍摄任务中具有相同目标景物的图像区域。根据上述内容可知,[0,Ts-δ]期间2#CCD拼接区与[δ,Ts]期间1#CCD拼接区所成的视差图像中具有相同的目标景物,提取上述2个图像区域用于图像处理,进而采用基于模块匹配和曲面拟合的图像配准方法,得到一组位置偏移量序列{p(n)}N,符号的定义同上。
1.2.2 采用对地探测坐标变换公式计算低频像移
工程参数包括卫星轨道高度、星下点经纬度、卫星三轴姿态角及角速度等数据。长春光机所王家骐院士提出的对地探测坐标变换公式,已成功应用于国内多台高分辨率空间相机中[25],结果表明该公式能够准确地将卫星在轨运行期间实时探测的工程参数转换为焦面像移。
值得注意的是,受限于各类工程参数传感设备的采样频率,目前卫星对工程参数的更新频率约为每秒2次(由中科院长春光机所提供)。根据奈奎斯特采样定理可知,由工程参数计算所得的像移数据中只包含二分之一采样频率以下的低频分量,进而采用插值方法得到与位置偏移量长度相同的低频像移序列{y1(n)}N。
1.2.3 建立基于拼接区图像和低频分量的目标函数并求解最小值点
依据平方误差理论,以低频像移序列{y1(n)}N和位置偏移量{p(n)}N为已知量,建立如式(1)所示的目标函数,用以衡量像移曲线与低频分量之间的偏差程度:
F(y(1),y(2),…,y(D),η)=Fwithout(y(1),y(2),…,
y(D))+Fwith(y(1),y(2),…,y(D),η)
(1)
式中:Fwithout(y(1),y(2),…y(D))描述了一次拍摄任务所成的视差图像中,无相同目标景物期间像移与低频分量之间的偏差程度;Fwith(y(1),y(2),…,y(D) )用于评价有相同目标景物期间[δ, (η+1) ×δ]时间段内的像移与其低频分量之间的偏差程度;其余符号的定义同上。
根据平方误差和最小的原理,本文构建无相同目标景物期间的目标函数:
(2)
式中各符号的定义同上。有相同目标景物期间[δ, ( +1)×δ]时间段内的目标函数如下:
(3)
式中扩展系数η描述了函数F在有相同目标景物期间的覆盖度,η∈N*,N*为正整数集,扩展系数η越大,函数F在有相同目标景物期间的覆盖度越广,对像移与其低频分量之间的偏差程度的约束越严格,如图3所示。下一步工作是针对扩展系数 对无相同目标景物期间像移估计的影响进行研究。

图3 扩展系数 对偏差约束程度的影响Fig.3 Effect of expansion factor on deviation constraint
目标函数F衡量了像移曲线与低频分量之间的偏差程度,函数值越小,像移与低频分量之间的偏差度越低,对应的无相同目标景物期间的像移更接近真实值。本文选取运算量最小的最速下降法筛选目标函数的最小值点Yopt,作为无相同目标景物期间像移的最优估计,即:
Yout=[y(1),y(2),…,y(D)]|minimize
{F(y(1),y(2),…,y(D),η)}
(4)
2 有相同目标景物期间的像移计算
由于相邻两片TDICCD的拼接区对同一目标景物的成像时刻不同,像移的取值和方向可能导致同一目标景物在拼接区所成的两幅视差图像中的位置存在偏差,如图4所示。

图4 位置偏移量的形成过程Fig.4 Formation of position offsets
位置偏移量衡量了同一目标景物在两幅视差图像中的偏移程度,其与像移之间的关系如下:
y(t+δ)=y(t)+p(t) 0≤t≤Ts-δ
(5)
式中:y(t)和y(t+δ)分别为t和(t+δ)时刻的焦面像移;δ为TDICCD拼接区对同一目标景物的拍摄时间差;p(t)为t时刻的位置偏移量。将(5)式中的时间变量t离散处理后得到:
y(n+D)=y(n)+p(n) (n=1,2,…,N)
(6)

Ywithout=[y(1),y(2),…,y(D)]T
(7)
有相同目标景物期间[δTs-δ]内的像移离散序列,以连续的D个元素为一组进行分组处理,则第1组像移为Y1=[y(D+1),y(D+2),…,y(2D)]T。根据(5)式可知,第1组像移可以表示为
y(D+i)=y(i)+p(i)i=1,2,…,D
(8)
令位置偏移量P1=[p(1),p(2),…,p(D)]T,可得:
Y1=Ywithout+P1
(9)
同理,第2组像移为Y2=[y(2D+1),y(2D+2),…,y(3D)]T。根据(5)式可知,第2组像移可以表示为
y(2D+i)=y(D+i)+p(D+i)
i=1,2,…,D
(10)
将(8)式代入(10)式可得:
y(2D+i)=y(i)+p(i)+p(D+i)
i=1,2,…,D
(11)
令位置偏移量P2=[p(D+1),p(D+2),…,p(2D)]T,则(11)式可以化简为
Y2=Ywithout+P1+P2
(12)
以此类推,第k组像移可以表示为
y(k×D+i)=y(i)+p(i)+p(D+i)+p[(k-
1)×D+i]
k=1,2,…,K,i=1,2,…,D
(13)

Yk=Ywithout+P1+P2+…+Pkk=1,2,…,K
(14)
式中无相同目标景物期间的像移可采用本文上述方法估计,位置偏移量数据可采用上述图像配准方法获得,根据公式(14)可确定有相同目标景物期间的像移。
3 实验及结果分析
XX-1号空间光学遥感器焦面上存在5片TDICCD交错拼接排布,拼接区存在40列重叠像元,行扫描周期约为65 μs,单次成像任务的时长约为29.18 s,其中无相同目标景物期间位于最初的226 ms以内。本文选取视场中心相邻两片TDICCD所成的遥感图像为实验对象,以北京(场景A)和云南(场景B)为研究区域,利用本文算法估计像移,并将结果分别与基于工程参数的方法和基于遥感图像的方法进行对比,分析本文算法的有效性。
图5显示了本文算法和基于遥感图像方法的像移时域曲线。从图5(a)和图5(b)的局部曲线可以看出,本文算法可检测的时间范围包含相机开拍最初的[0, 226 ms]范围,即无相同目标景物区间,而单纯利用遥感图像所测得的像移结果中不包含无相同目标景物区间。此外,虽然场景A和场景B中两种方法的像移曲线大体趋势基本一致,但仍然存在偏差,且偏差主要集中于高频分量,为此,将像移测量结果分为低频和高频两部分。
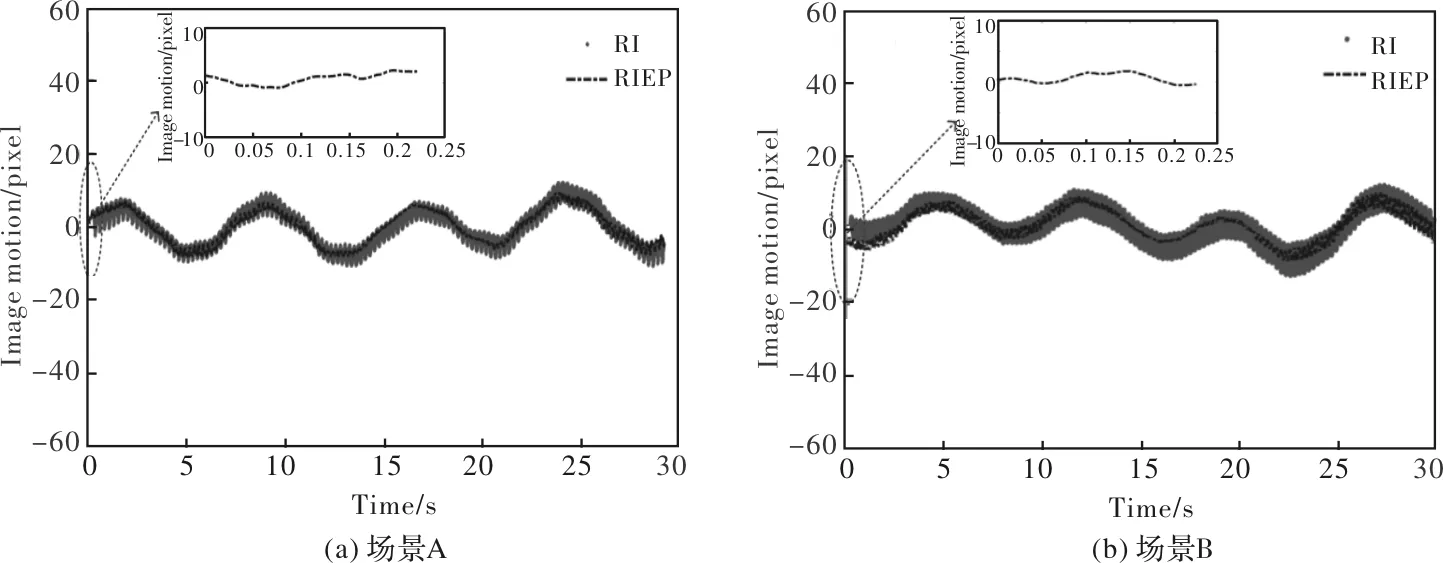
图5 时域像移测量结果(RI:基于遥感图像的像移测量方法;EP:基于工程参数的像移计算方法;RIEP:基于遥感图像和工程参数的像移测量方法)Fig. 5 Results of image motion in time domain(RI: Image motion method based on remote images; EP: Image motion method based on engineering parameters; RIEP: Image motion method based on remote images and engineering parameters)
由于卫星每512 ms更新一次工程参数,意味着单纯地利用工程参数,最高可恢复0.98 Hz的像移(1/512 ms/2=0.98 Hz)。本实验中每40行视差图像提取一个位置偏移量数据,相当于位置偏移量数据的采样频率为384.62 Hz(1/65 μs/40 lines=384.62 Hz),则从遥感图像中最高可提取192.31 Hz的像移。为此,将整个频率分为0~0.98 Hz低频和0.98 Hz~192.31 Hz高频2个区间。
在低频区间,将本文算法与基于工程参数的方法和基于遥感图像的方法进行对比,讨论3种算法在低频区间测量结果的一致性。从图6(a)和图7(a)中的幅频曲线可以看出,3种算法的峰值均出现在0.133 Hz处,虽然幅值存在一定差异,但基本可以确定该光学遥感器在对场景A和场景B成像期间,焦面上存在0.133 Hz、幅值约为7 pixels的像移,3种算法在低频区的像移测量结果基本一致,能够证明本文算法对低频区像移测量的有效性。
在高频区间,将本文算法与单纯基于遥感图像的方法进行对比,如图6(b)和图7(b)所示,两种算法均存在若干峰值点,从局部放大图可以看出,两种算法在峰值及其附近频率点处的振幅差别较大,而距离峰值较远的频率处的振幅基本一致。此外,从表1统计的峰值频率发现,两种算法的峰值频率非常接近,且都位于4.4 Hz的整数倍附近,而4.4 Hz恰恰是本实验中相邻两片TDICCD对同一目标景物的成像时间间隔δ的倒数(1/δ=1/(65 μs/行×3 480行≈4.4 Hz)。这是由于频率等于或接近1/δ的像移经过时间间隔δ之后,正好经历或接近整数倍周期,像移的取值与时间间隔δ之前的取值相差很小,导致同一目标景物在相邻两片TDICCD拼接区所成的两幅视差图像中的位置偏差很小,进而导致频率等于或接近1/δ的整数倍的像移难以准确探测,盲点一直是基于遥感图像的像移探测算法中普遍存在的问题[24]。
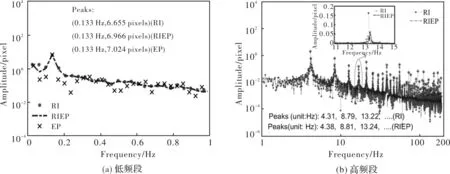
图6 场景A的频域像移测量结果Fig. 6 Results of image motion in frequency domain for Scene A

图7 场景B的频域像移测量结果Fig. 7 Results of image motion in frequency domain for Scene B
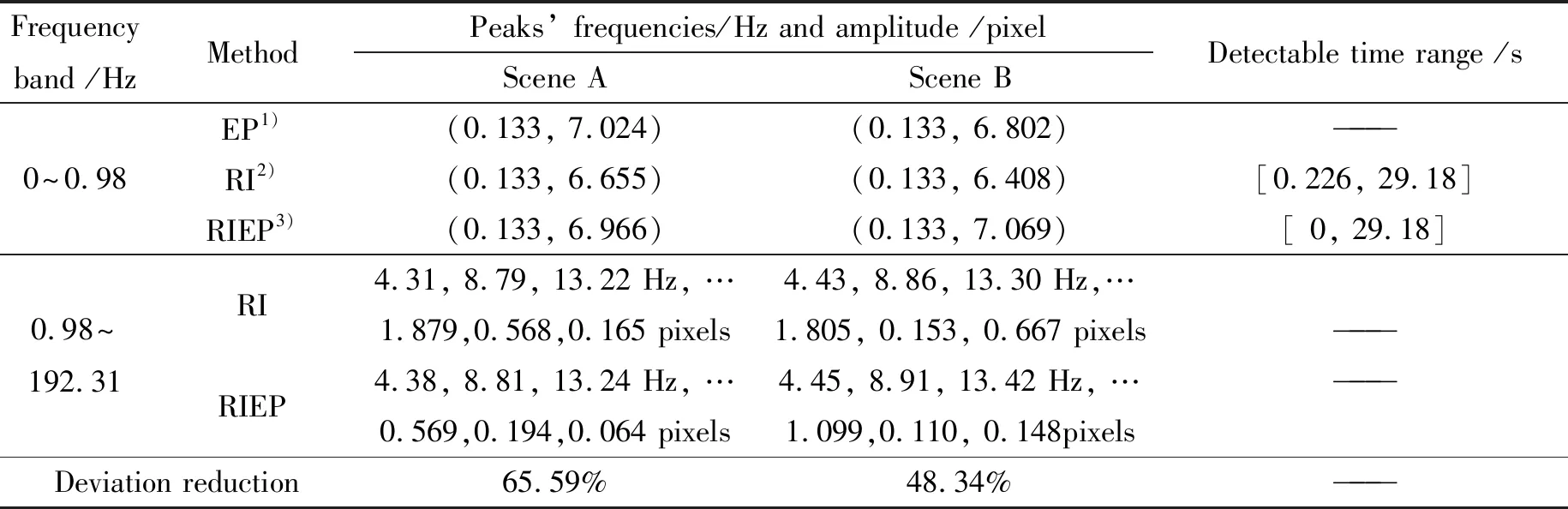
Frequency band /HzMethodPeaks’ frequencies/Hz and amplitude /pixelScene AScene BDetectable time range /s0~0.98EP1)(0.133, 7.024)(0.133, 6.802)———RI2)(0.133, 6.655)(0.133, 6.408)[0.226, 29.18]RIEP3)(0.133, 6.966)(0.133, 7.069)[ 0, 29.18]0.98~192.31RI4.31, 8.79, 13.22 Hz, …4.43, 8.86, 13.30 Hz,…1.879,0.568,0.165 pixels1.805, 0.153, 0.667 pixels———RIEP4.38, 8.81, 13.24 Hz, …4.45, 8.91, 13.42 Hz, …———0.569,0.194,0.064 pixels1.099,0.110, 0.148pixelsDeviation reduction65.59%48.34%———
注:1) 基于工程参数的像移测量方法;2) 基于遥感图像的像移测量方法;3) 基于遥感图像和工程参数的像移测量方法
根据表1的统计结果可知,在场景A和场景B的两组实验中,本文算法在盲点处的测量偏差分别下降了65.59%和48.34%。由此可见,与现有算法单纯地从遥感图像中提取像移信息相比,本文结合了空间相机在轨工作期间实时获取的工程参数,从工程参数中提取低频像移信息,并以最小方差为目标求解像移,显著地削弱了盲点处的像移测量偏差。
4 结论
相邻两片成像传感器的拼接区能够对同一目标景物先后成像2次,从而形成的图像中具有相同的目标景物,这是基于遥感图像方法获取像移信息的关键。然而,在成像初始阶段,相邻两片成像传感器拼接区输出的遥感图像中并无相同的目标景物,单纯地依赖遥感图像难以获取像移信息,为此,本文提出了基于遥感图像和工程参数的全局像移探测算法。利用国内XX-1号空间光学遥感器在轨实时拍摄的遥感图以及工程参数对算法进行了验证,结果表明本文算法的可探测时间范围包含无相同目标景物阶段。此外,在低频区,本文算法与现有算法的像移测量结果基本吻合,证明了本文算法对低频区像移测量的有效性;在高频区,与现有算法相同,依然存在对频率等于或接近1/δ整数倍处的像移难以准确检测的问题,但是,在距离1/δ整数倍较远的频率点处的像移测量结果与现有方法基本一致,证明了本文算法对高频区像移测量的有效性。另外,本文算法显著地削弱了盲点处的像移测量偏差。以上分析表明,除频率等于或接近1/δ整数倍的像移外,本文算法能够对包含无相同目标景物期间的全局像移进行有效测量,这对实现全局像移补偿,进而削弱像移对像质的影响具有重要意义。
