斜交T梁桥受力性能分析

唐 朝 阳

(福建省公路管理局，福建 福州 350002)

1 概述

随着道路建设不断完善，对桥梁的设计提出了更高的要求。在设计中，桥梁的平面布置需考虑线路走向，从而遇到的桥梁结构与常规的正交桥有所差异，最常见的有斜交桥、斜交曲线桥等。尤其是在周围环境限制的条件下，桥梁设计中需采用斜交梁桥以满足线形要求，如何准确掌握斜交桥梁的受力性能，成为设计首先需解决的关键问题。

斜交梁桥的研究主要是以简支斜梁桥为 主。目前在斜交梁桥的研究领域，国外已有相应的设计规范[1]。Kahleel等[2]指出在斜交角φ=60°的情况下，斜交梁桥内梁的最大弯矩相对正交桥减小29%，外梁的最大弯矩相对正交桥减小20%；Bishara等[3]研究表明横梁的数量在一定范围内对结构有益，并且当斜交角小于20°时可以按正交桥的受力特点进行分析。项贻强[4]归纳了斜梁桥截面形式的选择、主梁与横梁的布置形式、斜梁桥的分析方法和施工措施等。杨云芳[5]研究了简支斜梁桥和正梁桥受力的特性，表明斜交梁桥所受弯矩小于同一正交梁桥的弯矩，但尚未对多梁式简支斜交梁桥的受力特性进行分析。黄平明等[6]研究了端横梁的弯曲和支座变形对斜主梁所提供的弹性抗扭支承和竖向弹性支承。黄平明[7,8]研究了斜梁桥横向刚度，得到阶梯中的横梁刚度小于正交中横梁的整体刚度。周冬等[9]采用梁格法研究了恒载和移动荷载两种情况下，横梁内力在不同斜交角度下所受的影响。韩焜焜等[10]采用ANSYS有限元分析软件建立了异形斜交箱梁桥模型，得出斜交桥的边支座反力均小于异形桥的边支座反力。上述虽从许多方面对斜交T梁桥进行了深入的研究，但没有全面地分析斜交角的变化和支反力对斜交T梁内力的影响。

本文研究的斜交角度范围为0°～60°之间的桥梁，跨径均为30 m的简支斜交T梁桥，采用Midas civil 2015有限元软件建立模型，斜交角分别设置为0°，15°，30°，45°和60°五种情况，基于每种斜交角T梁数分别为3片、5片、7片和9片，相应的宽跨比分别为0.24，0.4，0.56和0.72。最后采用Midas civil 2015计算得出五种不同斜交角以及四种宽跨比影响下斜交T梁桥的弯矩和支座反力，进而分析斜交T梁桥的受力性能，其研究成果可用于指导简支斜交T梁桥的设计以及加固。

2 建立有限元模型

2.1 基本资料

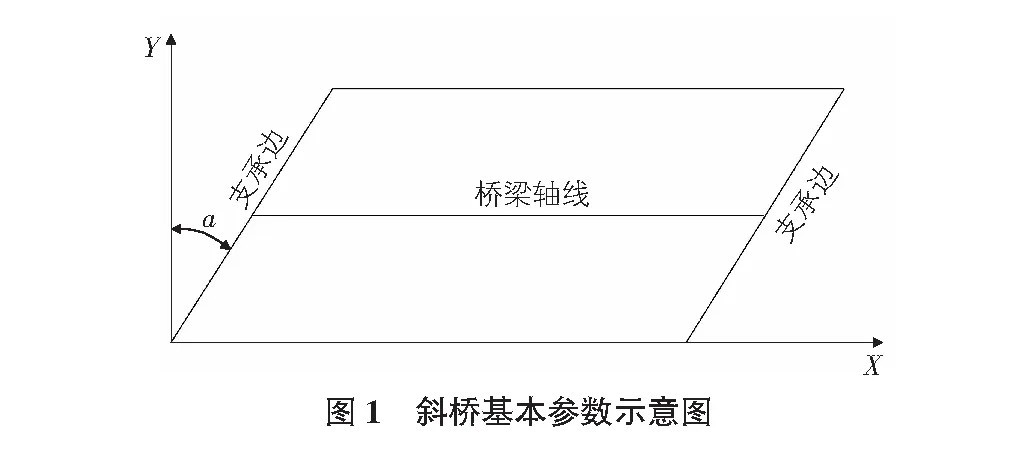
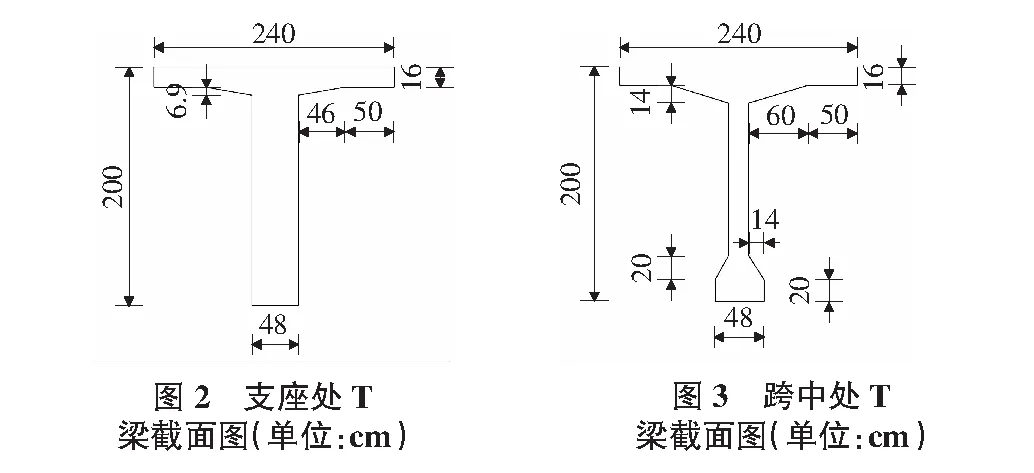
桥梁标准跨径为30 m，采用钢筋混凝土预制T梁，混凝土为C50，梁高为200 cm，翼缘厚度为16 cm，支座截面处肋宽为48 cm，跨中截面处肋宽为20 cm。斜交梁桥基本参数示意图如图1所示，T梁截面如图2和图3所示。

2.2 有限元建模

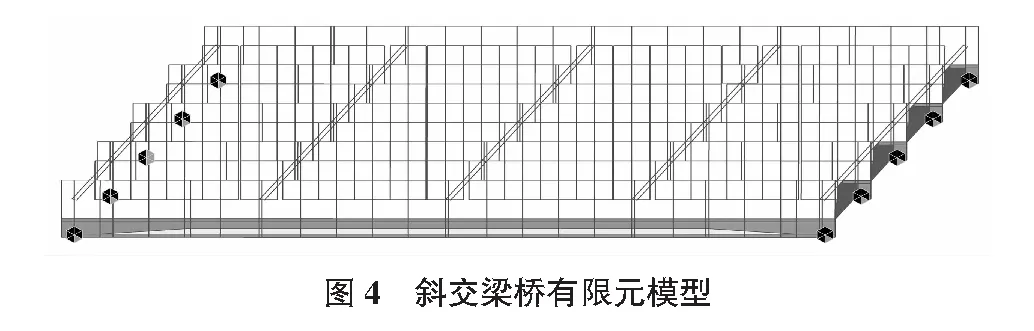
以斜交角φ=30°和宽跨比为0.4(5片)的简支斜交T梁桥为例，全桥共有177个节点和261个单元，其中梁单元有261个。主梁和横梁均采用空间梁单元进行模拟，每个单元包含2个节点，每个节点考虑3个平移自由度和3个转动自由度。

本文所建模型的边界条件为：T梁左边中梁的支座采用一般支撑约束Dx，Dy，Dz和Rx，其余支座和右边支座均约束Dz，T梁和桥墩之间采用弹性连接中的刚性连接。所有模型均考虑以下两个荷载工况：1)自重：C50混凝土重度为γ=26 kN/m3。2)汽车荷载：采用公路—Ⅰ级荷载，均布荷载标准值为q=105kN/m。

图4以φ=30°和宽跨比为0.4(5片)的简支斜交T梁桥为例，采用Midas civil 2015有限元软件建立模型。

3 结果分析

斜交角、扭矩、支承形式、宽跨比以及弯扭耦合作用是影响斜梁桥受力的主要因素，本文主要研究在荷载作用下斜交T梁桥边梁的弯矩变化情况，选取图1中最外侧的边梁作为研究对象，左支座在锐角处，右支座在钝角处[11]。

3.1 斜交角φ=0°时

当斜交角φ=0°时，即为正交梁桥，采用Midas civil 2015有限元软件分别建立宽跨比为0.24,0.40,0.56和0.72的简支斜交T梁模型，对应的T梁数为3片、5片、7片和9片，经运行分析所得数据如图5所示。

由图5可得，在荷载作用以及不同宽跨比情况下，边梁弯矩关于1/2截面基本对称，而且跨中最大弯矩随着宽跨比的增大而减小，而且在1/2截面处各宽跨比所对应的弯矩值相差最大，且左右支座均无负弯矩出现，符合正交梁桥的受力特征。

3.2 斜交角φ=15°时

当斜交角φ=15°时，采用Midas civil 2015有限元软件分别建立宽跨比为0.24,0.40,0.56和0.72的简支斜交T梁模型，对应的T梁数为3片、5片、7片和9片，经运行分析所得数据见图6。

由图6可得，在荷载作用以及不同宽跨比情况下，边梁弯矩关于1/2截面趋于对称，而且跨中最大弯矩随着宽跨比的增大而逐渐减小，在左支座处，即锐角处仅出现正弯矩，但在右支座处，即钝角处表现出正负弯矩；在1/2截面处各宽跨比所对应的弯矩值相差最大，且当宽跨比为0.24时，跨中的弯矩最大，为5 858.6 kN·m。

3.3 斜交角φ=30°时

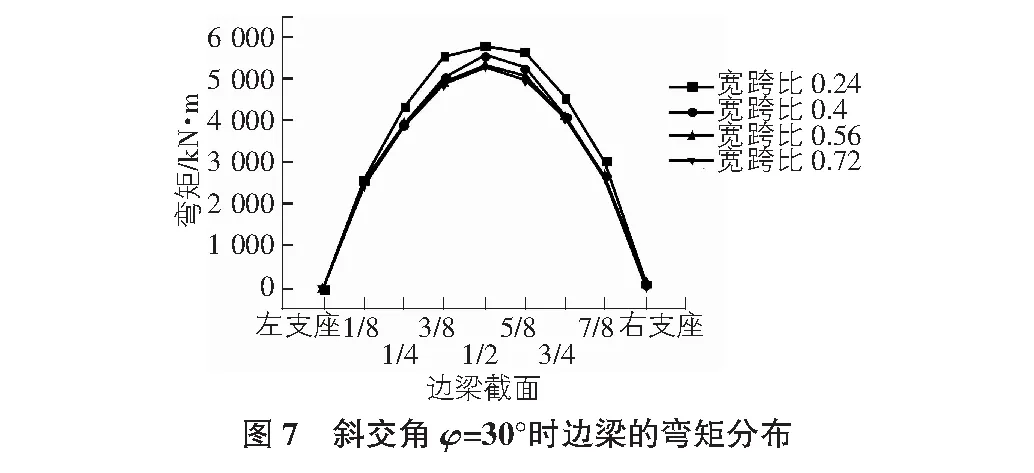
当斜交角φ=30°时，采用Midas civil 2015有限元软件分别建立宽跨比为0.24,0.40,0.56和0.72的简支斜交T梁模型，对应的T梁数为3片、5片、7片和9片，经运行分析所得数据如图7所示。

由图7可得，在荷载作用以及不同宽跨比情况下，边梁弯矩关于1/2截面趋于对称，而且跨中最大弯矩随着宽跨比的增大而逐渐减小，在左支座处，即锐角处仅出现正弯矩，但在右支座处，即钝角处表现出正负弯矩；在1/2截面处各宽跨比所对应的弯矩值相差最大，且当宽跨比为0.24时，跨中的弯矩最大，为5 812.2 kN·m。

3.4 斜交角φ=45°时

当斜交角φ=45°时，采用Midas civil 2015有限元软件分别建立宽跨比为0.24,0.40,0.56和0.72的简支斜交T梁模型，对应的T梁数为3片、5片、7片和9片，经运行分析所得数据见图8。

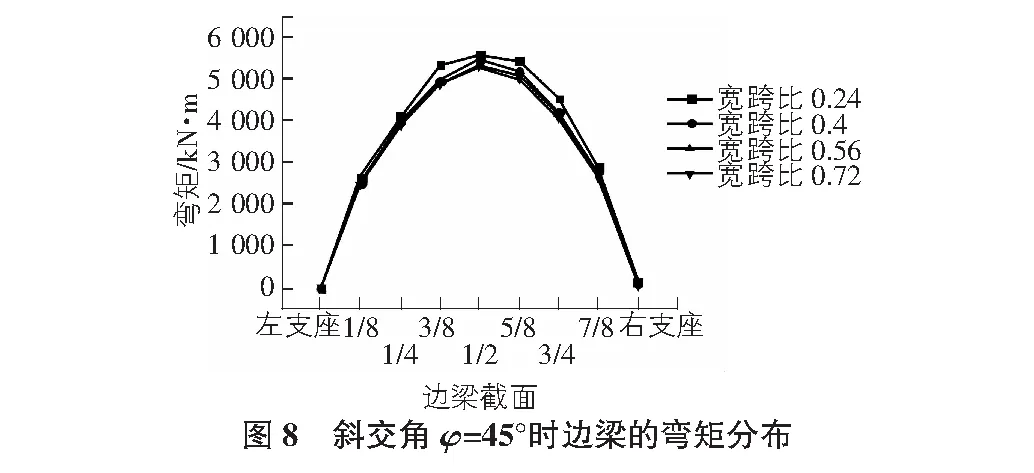
由图8可得，在荷载作用以及不同宽跨比情况下，边梁1/2截面左侧弯矩小于右侧弯矩，即锐角侧弯矩小于钝角侧弯矩，随着从跨中至支座其差值越明显，且相对于斜交角φ=0°最大弯矩有向钝角方向偏移；跨中最大弯矩随着宽跨比的增大而逐渐减小，在左支座处，即锐角处仅出现正弯矩，但在右支座处，即钝角处表现出正负弯矩；在1/2截面处各宽跨比所对应的弯矩值相差最大，且当宽跨比为0.24时，跨中的弯矩最大，为5 577.1 kN·m。

3.5 斜交角φ=60°时

当斜交角φ=60°时，采用Midas civil 2015有限元软件分别建立宽跨比为0.24，0.40，0.56和0.72的简支斜交T梁模型，对应的T梁数为3片、5片、7片和9片，经运行分析所得数据见图9。

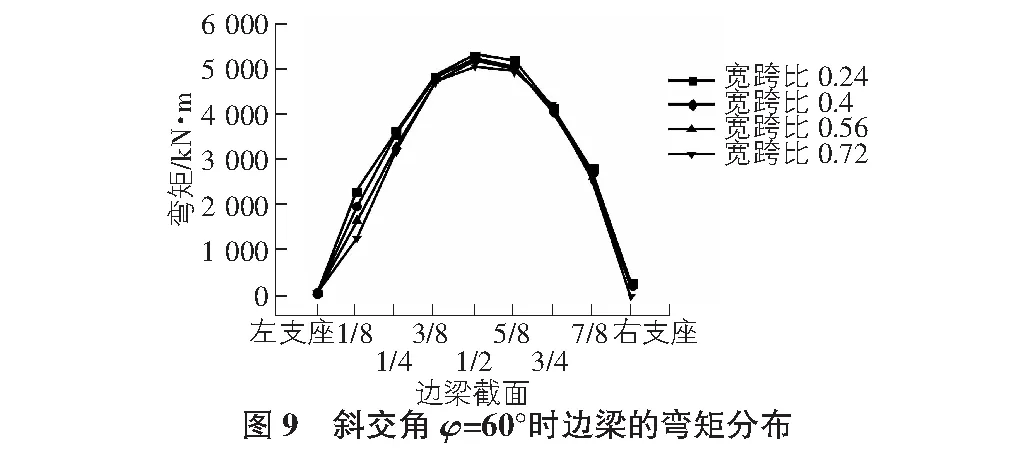
由图9可得，在荷载作用以及不同宽跨比情况下，边梁1/2截面左侧弯矩小于右侧弯矩，即锐角侧弯矩小于钝角侧弯矩，随着从跨中至支座其差值越明显，且相对于斜交角φ=45°最大弯矩向钝角方向偏移更显著；跨中最大弯矩随着宽跨比的增大而逐渐减小，在左支座处，即锐角处仅出现正弯矩，但在右支座处，即钝角处表现出正负弯矩；在1/2截面处各宽跨比所对应的弯矩值相差最大，且宽跨比为0.24时跨中的弯矩最大，为5 296.8 kN·m。

4 讨论

4.1 斜交角度变化与最大弯矩位置移动的关系

取0°,15°,30°,45°和60°中宽跨比为0.4(5片梁)的弯矩进行比较，分析最大弯矩位置的移动与角度变化之间的关系。

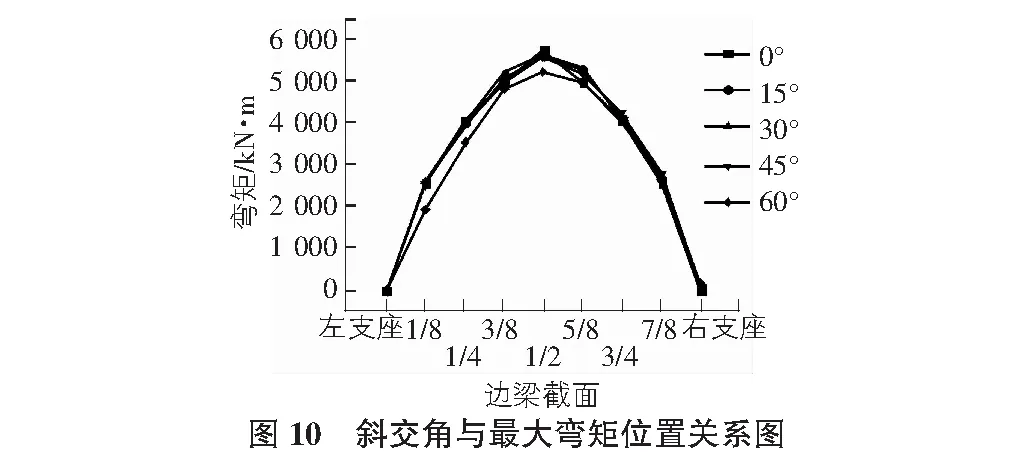
由图10可得，在荷载作用下，边梁1/2截面左侧弯矩小于右侧弯矩，即锐角侧弯矩小于钝角侧弯矩，随着从跨中至支座其差值越明显，斜交角为60°时，弯矩差值最为显著，差值最大为751.2 kN·m，由此表明同一宽跨比条件下，弯矩向钝角方向偏移。

4.2 斜梁桥与正梁桥边梁跨中弯矩比较

分别取斜交角为0°,15°,30°,45°和60°以及中宽跨比为0.24,0.4,0.56和0.72的弯矩进行比较，分析最大弯矩位置的偏移与角度变化、宽跨比之间的关系。

由图11可得，在荷载作用以及同一宽跨比影响下，边梁弯矩随着斜交角的增大而减小，且在宽跨比为0.24时相对于φ=0°最大减小10.6%；在荷载作用以及同一斜交角影响下，边梁弯矩随着宽跨比的增大而减小，且在φ=0°最大减小8.9%。

4.3 斜交角对支座反力的影响分析

取0°,15°,30°,45°和60°中宽跨比为0.4(五片梁)的弯矩进行比较，分析支座反力与角度变化之间的关系。

由图12分析可得，在荷载作用下，梁端钝角附近的支反力随着斜交角度的增大而增大，相对0°时最大增加10%；梁端锐角处产生的支反力随着斜交角度的增大而减小，相对0°时最大减小9%，但总体变化幅度较小。

5 结语

本文研究的斜交角度范围为0°～60°之间的桥梁，跨径为30 m的简支T梁桥，采用Midas civil 2015有限元软件分别建立斜交角为0°,15°,30°,45°和60°以及宽跨比0.24,0.4,0.56和0.72的模型，并对其进行数值模拟，分析斜交T梁桥随着斜交角和宽跨比变化时的受力规律,得到如下结论：1)随着斜交角发生变化，斜交T梁桥的受力特性逐渐发生改变，即斜交T梁的最大弯矩随着斜交角的增大往钝角方逐渐偏移，且当斜交角为60°时弯矩偏移最大。2)在荷载作用以及同一宽跨比影响下，边梁弯矩随着斜交角的增大而减小，且在宽跨比为0.24时相对于φ=0°最大减小10.6%。3)在荷载作用以及同一斜交角影响下，边梁弯矩随着宽跨比的增大而减小，且在φ=0°最大减小8.9%。4)最大负弯矩出现在支承截面处，且当斜交角为60°时负弯矩最大，-100 kN·m。5)梁端钝角附近的支反力随着斜交角度的增大而增大，相对0°时最大增加10%，梁端锐角处的支反力随着斜交角度的增大而减小，相对0°时最大减小9%，但是总体变化幅度较小。

综上所述，在同一荷载作用下，简支斜交T梁桥的钝角部位较锐角处容易破坏，在进行设计时应采取相应的措施予以加固。