借由多种表征,建立小数与十进分数的联系
——《小数的初步认识》教学实践与思考
2019-10-14符玲利章勤琼
□ 符玲利 章勤琼
【课前思考】
三年级学生已经初步认识了分数,知道将一个物体平均分成几份,表示其中的一份或几份可以用分数来表示;他们也具备1元=10角、1米=10分米的生活经验,了解一些简单价格表示的意义,如0.1元是1角。但为什么1角用0.1元来表示呢?1元等分成10份,1份是1角,学生顺向思考好像没有问题,但逆向思考1角是十分之一元却出现障碍,认知出现断层。如何将小数的意义和生活经验建构起来,需要通过十等分来做支撑。故本课选择学生熟悉的人民币、长度单位等素材,试图在学生已有认知基础上建立起十等分的概念,再借助操作提炼出一位小数的意义。
【教学内容】人教版三年级下册第七单元
【教学目标】
1.结合具体情境初步认识小数,会读、写小数,知道一位小数表示的意义。
2.经历观察、操作、辨析等过程,沟通分母为10的分数与一位小数之间的联系,培养学生的数感,渗透一一对应思想。
3.在交流的过程中充分发表自己的想法,培养勇于质疑的精神,形成严谨求学的科学态度。
【教学过程】
一、导入新课,初悟小数
1.谈话导入
师:同学们,一年级小朋友上课时遇到一个问题,他们的书上出现了一些不认识的数(如下图),你认识吗?

生:都有小数点。
生:不是,是小数。
师:是的,这些数叫小数,小圆点叫小数点,小数点左边是整数部分,小数点右边是小数部分。(板书课题:小数)
2.读小数
生:第一个是2元。
师:哦,固体胶的价格是2元,就读作2元吗?
生:二点零零元。
师:一起来读后面几个价格。
生齐读:零点五零元(零点五十元)。
师:我听到两种声音,小数部分的读法和整数部分一样吗?(学生无法肯定)其实小数部分的读法和整数部分不一样,小数部分要一个一个读,再来读一次。
生齐读:零点五零元、五十九点九零元,九点二五元。
3.生活中小数的意义
师:0.50元中的5表示什么意思?9.25元中的5又表示什么意思?
生:0.50元中的5表示5角;9.25元中的5表示5分。
师:59.90元中的两个9分别表示什么意思?
生:59.90元中整数部分的9表示9元,小数部分的9表示9角。
(思考:小数在生活中比较常见,学生并不陌生,结合具体情境学生能表述出各个数位上小数代表的实际意义,挖掘学生的生活经验,为后续深入理解小数做铺垫。)
二、数形结合,理解小数
1.实物表征,初步理解
师:1角=?元。
生:1角就是0.1元。
师:1角是0.1元,你是怎么想的?
生:1元=10角,1角=0.1元。
师:为什么?
生:1元里有10个1角,1角不够1元,它只是这10个1角中的一个。(师课件呈现)

生:1元=10角,相当于把1元平均分成10份,这1角就是10份中的1份,所以用0.1元表示。
师:把1元平均分成10份,取其中的1份,我们好像学过?
师:3角=?元。
生:1元里有10个1角,3角是10份中的3份,是0.3元。
2.线段表征,加深认知
师:(呈现1米线段)这是1米的线段,1分米和1米有什么关系?

生:1米=10分米,把1米平均分成10份,其中的1份是1分米。
师:在1米的线段中你还能找到哪些小数?请你分一分,找一找。
学生尝试后反馈找到的小数:0.3米、0.6米、0.9米。
生:把1米平均分成10份,取1份就是0.1米,取3份就是0.3米,取6份就是0.6米;其中的9份就是9分米,也就是0.9米。

生:把1米平均分成10份,取几份就是零点几米。
(思考:1元=10角,那1角等于多少元?带着疑问学生主动寻找小数产生的原因。慢慢地学生发现,1角不能用整数元来表示,因为1角不足1元,1角是1元的。同理,1分米是1米的,把1元或1米等分成10份,表示其中的一部分时,小数就产生了,继而将与0.1产生联系。只有学生自身开始关注小数产生的过程,他们才能关注到十进制对于小数的意义。)
3.多种表征,理解本质
师:生活中我们找到了很多的小数,如果用一个正方形、长方形或是圆来表示1元钱,你还能找到0.3元吗?
学生操作、反馈:
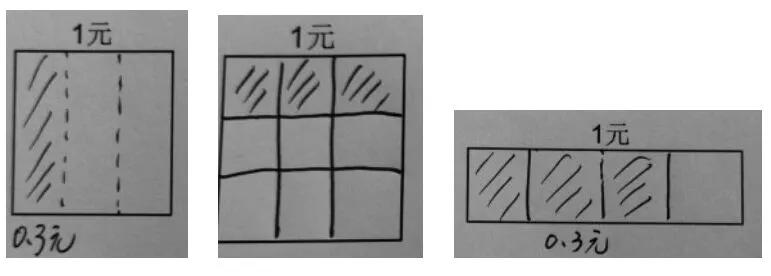
师:这几位同学眼中的0.3元你看懂了吗?你想跟他们说什么?
生:他们没有平均分成10份,0.3是要先平均分成10份,再取其中的3份。

师:这些图中的涂色部分能用0.3元来表示吗?为什么?
生:可以的,因为1元=10角,只要把1元平均分成10份,然后涂出3份,就能表示出0.3元了。
师:刚才我们用1个正方形代表1元,找到0.3元;如果用这个正方形代表1米,那么0.3米该怎么表示?

师:这个正方形还可以代表什么?涂色部分该用哪个数来表示?
生:把这个正方形当作1千克,平均分成10份,涂其中3份就是,也就是0.3千克。
生:把正方形看成1平方米,平均分成10份,10份中的3份就是0.3平方米。
生:只要等分成10份,取3份就是0.3。
师:在这个正方形里你还能找到其他小数吗?
生:0.1 ,0.2,0.4,0.5,0.6,0.7,0.8,0.9。
生:只要把正方形等分成10份,取几份就是十分之几,就是零点几。
师:0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,再取1份呢?
生:就是1。
(思考:结合具体情境,学生容易发现小数的具体意义,但抽象地理解小数是十等分的结果,对学生而言是有难度的。在具体情境中理解十等分可以得到小数后,再安排学生画一画0.3,脱离具体的情境,关注本质,抽象出0.3的意义。安排1和0.3的对比,凸显0.3是1的十分之三,加深对一位小数的理解。)
三、数轴找数,培养数感
1.找相应的数
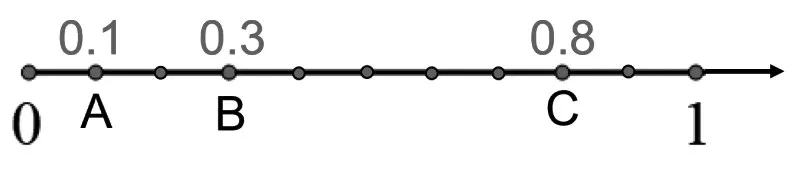
师:如果把米尺变成数轴,在0和1之间有3个点A、B、C,哪个点可能表示的是0.3?

生:B点,因为A离0太近,可能是0.1,C离1很近,可能是0.8。
师:怎么知道B点是不是0.3呢,你有什么好办法?
生:画画看,验证一下。
生:把这条线段平均分成10份,B点正好是3份,所以B点是0.3。A点是0.1,C点是0.8,也就是。
2.找更多的小数
师:把数轴再延长,1和2之间又会有哪些小数,请你找一找。
反馈学生的作品。

作品1

作品2
师:这里有两种不同的答案,你认可哪一种?
生:因为1到2之间又有一个1,把1平均分成10份,1份就是0.1,2份就是0.2,几份就是零点几。
生:不对,1和2之间平均分成10份,1份是0.1,但是它是在1后面再多0.1,所以应该是1.1,再往后数就是1.2,1.3……
师:数轴上还会有哪些小数?
生:2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9……
师:1和1.1之间你觉得还会有小数吗?
生:应该会有的,只要再平均分成10份就会有了,比如1.01。
师:你们太棒了,在数轴上除了有我们学过的整数,今天我们知道这些整数之间还有很多的小数,小数和整数让数轴变得更丰满。
(思考:在0和1之间判断哪个点可能是0.3,可检验学生对0.3的理解情况,也能培养学生的数感。在1和2之间找小数,既能检验学生是否真正理解十等分的概念,又能让学生感悟在相邻两个整数之间还有小数,数轴上除了整数还有小数。在数轴上找数,既能渗透数与点的一一对应性,又能培养学生的数感。)
四、回顾全课,渗透文化
1.这节课你有什么收获
生:把1等分成10份,十分之几就是零点几。
生:数轴上有很多很多的小数和整数。
2.小数的历史
师:你知道古时候人们是怎么表示小数的吗?

生:两竖表示2,横一表示1,竖五表示5,这个数是2.15。
师:为什么1要横着摆?
生:把小数和整数部分分开吧。生:太麻烦了,还是小数点好。师:古代的人还是很聪明的,不过小数点让数学变得更简洁,小数点是了不起的发明。
