让学生拥有完整的解决问题经验

2019-11-05平国强

教学月刊(小学版) 2019年26期

□ 平国强

解决问题能力是学生数学能力的核心，是学生综合运用数学知识和相关经验，展开分析比较、建立联系等一系列思维活动的结果。小学数学解决问题能力的提升过程是指学生通过基本方法、经验和问题的学习逐步提高能力，逐渐丰富方法，最终能够正确合理、自主灵活解决高水平问题的过程。在这个发展过程中，有效经验的支持至关重要。

一、合理的经验积累是解决问题的基础

数学教学的最终目的是提升学生的数学素养，即发展数学思维，提高数学能力，让学生能真正解决数学问题。学生解决问题的过程是一个信息梳理、问题识别、经验调用、联系沟通、关系表征、策略应用、方法确定和回顾反思的过程，这个过程，体现了以“已知”获得“未知”的思维路径。可以用下图来描述：

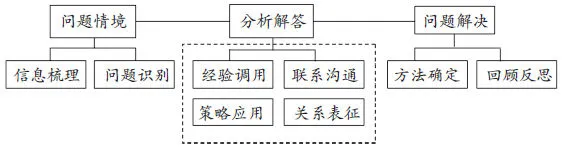
本质上，解决问题的过程就是一个数学推理的过程。要完成这个推理过程，学生需要一些必需的储备经验做基础。如果是一个合情推理过程，学生需要积累与理解一定的类似案例，才能做出合理的猜测与类比；如果是一个演绎推理的过程，学生需要有相应的数学问题的类型、特征、数量关系、解答方法及意义关联等经验积累作为推理的前提，我们不妨把这样的经验称为解决问题的基础性经验。学生解决问题能力的高低，很大程度上取决于学生经验结构中的基础性经验的完整性与合理性，以及策略性经验水平的高低。以人教版数学五年级上册《简易方程》中的例5为例，可以用下图直观地表达这样的观点。

可以发现，学生在解决问题时所要调用的储备经验，不仅仅是简单问题的经验，更重要的是基本与典型问题的特征与模型。因此，在解决问题教学中，我们有必要去研究“学生是否已经具有以上虚线框中的经验结构与储备”“如何让学生更好地拥有这样的经验储备”等问题。

二、学生应具有的储备经验内容分析

我们认为，学生在解决问题时需要调用两方面的经验，一是起着重要支持作用的基础性经验，二是表现为更高效率和更高水平的策略性经验。

（一）基础性经验

基础性经验在学生解决问题经验系统中处于概念与意义之上的层次，是培养更高的解决问题能力不可逾越的层次，是经验结构中不可或缺的部分。它来自于对各种有典型特征和模型的数学问题解决过程的经历与积累，是对各类基本和典型数学问题的特征、思路、结构与解决方法的熟悉和掌握。数学的学科特质决定了数学的典型和基本问题是具有类型与结构特征的，数学解决问题常常是将新问题转化为经验系统中所熟悉的问题来解决的，这正是化归思想是数学的重要思想的原因所在。因此我们认为，学生的基础性经验中应该具有：（1）对基本的、典型的数学问题的类型、特征有较好的领悟与积累，能正确地识别与关联；（2）对这些数学问题的基本结构和关系模型有较好的领悟与积累；（3）对这些数学问题的解题思路、思维关键和解决过程有较好的理解与把握；（4）对基本的画图表征数量关系、列表分析对应关系或提炼概括已知与未知之间的关系式等解决问题的具体方法有较好的掌握与积累。例如，对于以下一组问题：

题1：地球表面陆地的面积大约是1.5亿平方千米，海洋面积是陆地面积的2.4倍，地球表面的面积大约是多少亿平方千米？

题2：小明今年12岁，妈妈的年龄是小明的3倍，妈妈比小明大几岁？

题3：公园里有桃树45棵，柳树的棵数是桃树的1.6倍，两种树共有多少棵？

应该让学生通过对以上问题的解决，发现并领悟一些共性：（1）这些问题虽然情境不同、数据不同，但问题的数学特征和结构关系是类似的：问题信息都涉及一个数量及这个数量的几倍，所求问题是它们的和或它们的差；（2）这些问题隐含的关系和结构可以用以下方式表达出来：一个量+这个量的几倍=“问题”（注：“问题”是指回答题目中问题时的相应数量，下同）或一个量的几倍-这个量=“问题”，如果用▲表示一个数量，用★表示它的几倍，以上关系可以简化为：▲+▲×★=“问题”或▲×★-▲=“问题”，还可以表示为：▲×（1+★）=“问题”或▲×（★-1）=“问题”，这是和倍问题的基本模型。如果学生对这些问题的特征、结构关系等有较好的理解和识别能力，那么他们在解决以下问题时便有了很好的经验基础与数量关系模型储备，问题便能更顺利、更有效地解决。

题4：地球的表面积为5.1亿平方千米，其中海洋面积为陆地面积的2.4倍，地球上的海洋面积和陆地面积分别是多少亿平方千米？

题5：小明妈妈比小明大24岁，今年小明妈妈的年龄是小明的3倍。今年小明和妈妈各几岁？

题6：苹果和梨一共168千克，梨的数量是苹果的1.8倍，梨比苹果多多少千克？

……

（二）策略性经验

策略性经验是学生解决问题经验体系中重要的组成部分，一方面，它是与基础性经验并列并且在解决基本的、典型的数学问题过程中起着重要的支持作用的经验；另一方面，学生在运用高阶思维解决更高水平、更具挑战性的数学问题时，策略性经验将发挥更大的作用，它能使解决问题的方法更加多样，思维更加简洁、巧妙与直观，过程更具有效性和创造性。如果说扎实的基础性经验保证了学生解决问题能力的底气的话，那么，丰富的策略性经验则使得学生在解决问题时更具有灵气，更拥有智慧，它能有效地促进解决问题能力与水平的提升。因此，我们认为，策略性经验至少应该包括以下几个方面：（1）多样化、多手段分析表征数量关系的经验；（2）正确确定标准，将较复杂或较隐蔽的数量关系转化为标准统一、关系清晰、利于表征的经验；（3）运用类比解决问题、建立联系、深化理解的经验；（4）创造性解决问题的经验等。例如，四年级的学生解决以下问题：

张师傅要加工一些零件，如果每小时加工12个，完成任务需要6小时。但张师傅离下班还有4小时，如果他要在下班前完成加工任务，那每小时要加工多少个零件？

如果能够用一维的线段图分析表征数量关系，这自然很好，如下图：

加工的零件数：

但如果同时又能够把加工零件的总数看作是一个固定的长方形面积数，将每小时加工零件数和时间分别看成是这个长方形的长和宽，用二维的视角来表征问题中的数量关系，那么分析问题的思路与策略就变得丰富了，长方形从一个学习内容、计算对象变成了解决问题的手段，知识的应用性得到了凸显。如下图：

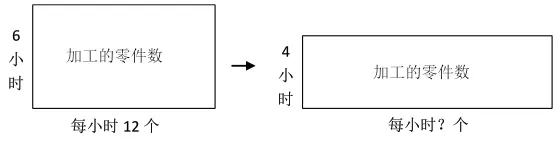
以上两种分析策略，并非仅仅是一种并列的、数量上的增加，后者与前者相比，反映出解决问题的思维水平从一维累计、比较直观的状态向更加数学化和模型化的方向发展，这无疑是学生解决问题经验结构中的高水平经验，对后续的数学能力与素养的发展非常重要。当然，如果学生能够通过思考推理提炼出以下数量关系表达式，同样是极为重要的经验和能力。

因为加工零件的数量是不变的，即“每小时加工12个×6小时=每小时加工（）个×4小时”，所以“每小时加工（）个=12×6÷4”。

所以，要让学生拥有这样丰富的分析问题、解决问题的策略经验积累，平时的教学应立足于策略、手段的多样化而非仅仅按部就班地复制教材。再比如六年级上册百分数的例5：

某种商品4月份的价格比3月份降了20%，5月份的价格比4月又涨了20%。5月份的价格和3月份比是涨了还是降了？变化幅度是多少？

事实上，无论是先降后涨还是先涨后降，只要涨和降的百分数相同，结果总比原价要低。这个问题看起来似乎是一个孤立的问题，但事实上，知识间的联系是客观与普遍的，如果我们用类比的策略思考，就可以发现：如果每次上涨和下降的百分数是a%，则最终的价格必定是原价的（1+a%）×（1-a%），这个算式与三年级研究过的“长方形的周长不变，长与宽怎样变化，它的面积最大”这个问题有类似性，如果把原价看作是一个边长为1的正方形，那么两次变化以后的价格相当于把正方形变成了周长相等的长方形，在这种情况下，正方形的面积总是最大的。如下图：

这样的一种联系思考，显然有助于学生更好地理解与把握六年级这类问题的特征与规律，使经验结构更优化，这既是一种类比的策略，也是一种重要的模型化联系与思考的经验。

三、教材内容的分析与实践

一般来说，学生解决问题的学习是一个从基本、典型问题到发展、变式问题的过程，从特征、模型的正向运用到逆向运用的过程，分析问题的策略方法也是从单一到多样的。如果学生能够完整经历以上的学习和能力发展过程，那么解决问题的经验结构就会比较完整，比较丰实，为更高水平的能力发展提供扎实的基础。我们以小学数学解决问题中的两类典型问题即“和倍问题”与“两积之和问题”为例，理想的经验积累过程应该是：

第一阶段学习理解问题的基本特征、数量关系和基本模型，能够分析数量关系，运用模型解决问题，为解决逆向或变式问题积累经验和倍问题两积之和问题例：小明的书柜里有36本书，爸爸书柜里书的本数是小明的3倍，两个书柜里一共有多少本书？模型：用■表示问题□+□×☆=■或□×（1+☆）=■例：星期天上午9:00，小林和小云同时从家里骑自行车出发，小林的速度是250米/分，小云的速度是 200米/分，9:10两人在公园相遇。他们一共骑了多少千米？模型：用■表示问题□×☆+△×☆=■或（□+△）×☆=■第二阶段学习判断与识别问题的特征和数量关系，能调用经验和模型结构建构相等关系，或逆用模型解决问题例：地球的表面积为5.1亿平方千米，其中海洋面积为陆地面积的2.4倍，地球上的海洋面积和陆地面积分别是多少亿平方千米？模型：用■表示问题（用方程解）■+■×☆=□或■×（1+☆）=□例：小林家和小云家相距4.5千米，周日早上9：00两人分别从家骑自行车相向而行，小林每分钟骑250米，小云每分钟骑200米。两人何时相遇？模型：用■表示问题☆×■+△×■=○或（☆+△）×■=○（用方程解）

对于逆用模型解决问题，目前课程标准的基本要求是列方程解，因此学生解决问题时完全以第一阶段的数量关系和基本模型经验为支持，顺着信息之间的关系和原来解决问题的思路去构造相等关系和方程，这样既突出了代数思想，又降低了学习的难度。

但是，仔细分析一下教材解决问题的例题与内容编排，可以发现：类似第二阶段学习内容教材有较多的编排，主要在五、六年级，但类似第一阶段学习内容教材基本没有编排，并且四年级整一年几乎没有学习上述基本的解决问题内容（笔者查阅了台湾翰林出版社和康轩文教事业两个版本的小学数学教材，或多或少都有类似内容的编排）。这在一定程度上使学生的解决问题经验结构存在某些薄弱环节，同时也提醒我们，在解决问题教学中，对教材的分析、补充和完善还有很大的空间。因此，我们认为，为促进学生解决问题经验体系更加完整合理，可以利用三、四年级的阶段，特别是四年级的空当，补充、丰富基本的、典型的解决问题内容学习，以加强基础性经验的积累。

第一，要丰富学生运用多种策略理解、分析信息与关系的经验。

例1：周六，奇奇和红红约好去看电影。9：30他俩同时从家里出发，相对而行，5分钟后两人在电影院相遇，9:40开始看电影。看完电影，奇奇去奶奶家吃饭。奇奇先走了2分钟，奶奶也出发来接奇奇。又过了3分钟，奶奶和奇奇相遇。

（1）奇奇和红红两家相距多少米？

（2）电影院离奶奶家有多少米？

这是一个有丰富信息和多个问题的情境，教学中教师要引导学生用多种方法理解题目的信息，分析关系。例如，如果要解决第（1）个问题，怎样在题目中用“圈”“画”等方法找到对解决问题有效的信息？如何用摘录的方法正确、完整地摘录有效信息和问题，并把它们清晰地呈现出来？如何用画图的方式把数量关系表征出来，让人一看就明白已知的信息和所求的问题？……这些都是应该要让学生拥有的方法与经验。

第二，要增加学生对基础的、典型的数学问题的特征、数量关系、表征方法和模型的积累。

例2：公主裙每件178元，老师买了2件公主裙和3箱牛奶，一共付了551元。牛奶每箱多少元？

教学中教师要求学生用自己的方式把问题的数量关系表示出来，下面是几位学生的分析表征：

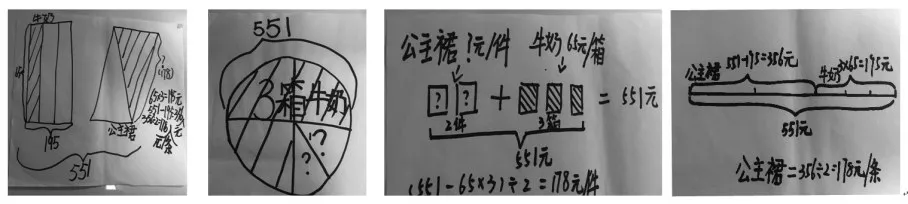
这是一个典型的两积之和问题的数量关系，如果学生能用如此多元的方式表征这种关系，表明学生对问题特征和数量关系的理解已非常清楚，并成为有效的经验与能力。

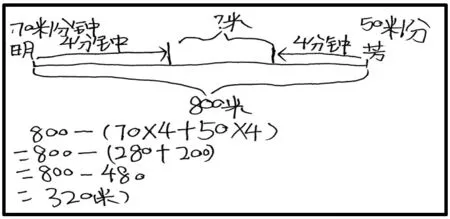
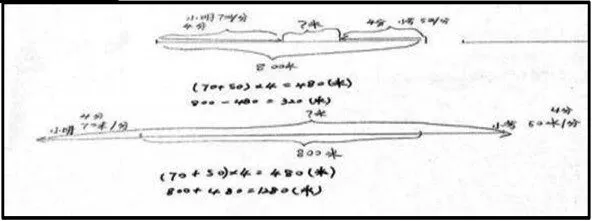
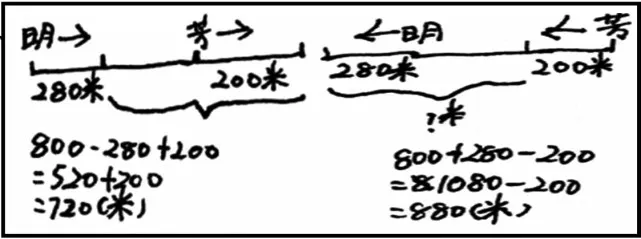
例3：小明和小芳两家相距800米。他们两人同时从家里出发，沿一条直路行走，小明每分钟走70米，小芳每分钟走50米，4分钟后他们相距多少米？

在这个问题中，两人的运动方式可能有哪些情况？每种情况是怎样的关系？有什么特征？如何把它们表征出来？……这些都涉及学生对信息、问题的认识、理解与把握。下面是学生的分析，表明他们已能较好地把握这类问题。

第三，要丰富学生分析问题、解决问题的策略积累。

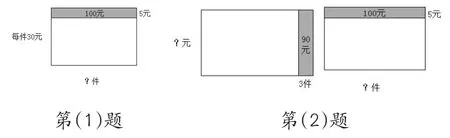
除了常用的直观图、线段图等方法以外，应让学生拥有更多的方法体验，例如用画长方形来分析数量关系、解决问题就是很重要的方法。比如：（1）合唱队计划买一批上衣，每件30元。如果每件降价5元，就可以节省100元。合唱队员计划买上衣要用多少钱？（2）合唱队计划买一批上衣，如果多买3件，就要多付90元，如果每件降价5元，就可以节省100元。合唱队员计划买上衣要用多少钱？这两个问题的关键都是上衣的件数，当然可以用多种策略来分析解决，但如果用画长方形来分析问题、解决问题，就更能体会到数学问题的模型化特征。如下图所示：