在归纳猜想中完成建模——记“找次品”内容的拓展教学

□ 朱海锋

“找次品”是人教版五年级下册数学广角的内容，教师都会用从特殊到一般的归纳推理方法进行教学。下面是笔者利用数学拓展课，对在不知次品轻重的前提下“找次品”教学的尝试。

一、第一次归纳猜想，尝试建模

在不知次品轻重的前提下“找次品”的课堂探索，相对知道次品轻重“找次品”来说，推理过程更加烦琐，所以拓展课上，笔者尝试分步带领学生进行猜测、讨论和尝试，从而让探究过程一步步走向深入。

（一）“三分法”是否还适用

在知道次品轻重的前提下，“三分法”是“找次品”问题解决的核心方法，因为当总量n=3时，称1次，或是，都能找出次品。在此基础上，有总量n=3a时的最少称的次数找出次品的推论，并进一步建立解决该问题的数学模型。

那么在不知次品轻重的前提下，“三分法”是否还适用呢？我们用总量n=6进行了对比讨论。

当n=6时，用“两分法”可分为6（3，3），称第1次时必然不平衡，但是由于不知次品是轻还是重，所以不能确定次品在哪一堆里，所以这一次称的过程没有起到应有的作用。而用“三分法”分为6（2，2，2）的话，称第1次会出现两种情况：如果天平平衡，则说明①②③④都是正品，次品在天平外面的⑤和⑥中，次品的范围已经从6个缩小到2个；如果天平不平衡，则说明外面的⑤⑥是正品，次品的范围从6个缩小到4个。

由此可见，在不知次品轻重的前提下，也需要把总量“三分”，从而找到其中一堆正品，当成标准量来进行比较。可见，用无砝码的天平找次品，关键是“三分”。

（二）选择哪些总量进行研究

由于推理过程比较复杂，所以拓展课中没有按人教版教材中已知次品轻重的前提下“找次品”的总量n=3，n=8，n=9这样进行探究，而是选用了“找次品”复习整理中的结论，从关键的总量n=3，9，27，81……也就是3的乘方数开始研究。

当 n=3 时，3（1，1，1）第 1 次称如果天平平衡，则次品是③，但不知③的轻重；如果天平不平衡，则证明③是正品，次品在①或②中，需要用正品③作为标准量，再与其中的①或②称1次，如果平衡，说明次品是外面的②，并且次品②轻，如果天平不平衡，则次品是①，并且次品①重。由此可见，在不知轻重的前提下，当n=3时，需要称2次。

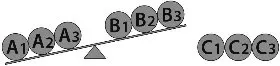
当n=9时，9（3A，3B，3C）称第1次，如果天平平衡，则3个A和3个B都是正品，次品在外面一堆的3个C中，并且不知道次品C的轻重，需要用“3A”作标准量，与“3C”再称第2次，就能知道次品是轻还是重了，然后再称第3次即可找出次品；如果天平不平衡（比如“3A”重于“3B”），则证明外面的“3C”是正品，需要用“3C”作为标准量，再与“3A”称第2次，若平衡则次品在“3B”中，并且次品轻，再称1次即可找到次品；若不平衡，则次品在“3A”中，并且次品重于正品，再称1次也可找到次品。所以，当n=9时，称3次能够找到次品。

同理，当n=27时，27（9A，9B，9C）称第1次，若平衡，次品在“9C”中，并且不知轻重，由上面推论可得：称3次能找到次品；若不平衡，用“9C”作为标准量与“9A”称第2次，就能找到次品是在“9A”中还是在“9B”中，再称2次即可找到次品。所以，当n=27时，称4次能够找到次品。

（三）学生的第一次猜想

根据以上分析，学生能很快地整理出一组相对应的数据（如下表）。

待测总量n 知道轻重的前提下需要称的次数不知轻重的前提下需要称的次数3 9 2 7 81……1 2 3 4……2 3 4 5……

第一节拓展课，学生就有了一个猜想：在不知次品轻重的前提下，保证找出次品所需称的次数，正好是知道次品轻重的前提下所需称的次数+1。再次对上面的数据进行验证，发现总量n=3，9，27，81时全都正确，经推理总量为243或者更大时，发现猜想也是正确的。

二、第二次归纳猜想，丰富模型

第二节拓展课，在特殊总量3，9，27等3的乘方数基础上，对其他总量进行进一步研究。

（一）发现猜想错误

在对别的总量如n=4、5、6等数进行研究，以验证我们上一节课的推论时，意外发生了。

当n=4时，4（1A，1B，2C）称第1次，如果天平平衡，则次品在外面的2个C中，然后A与C1称第2次，若平衡，则次品是C2；若不平，则次品是C1。称第1次，如果天平不平衡，则外面的C1、C2是正品，然后用正品C1与A称第2次，若平衡，则次品是B；若不平衡，则次品是A。

这个时候，学生开始茫然了，按照上一节课的推论，不知次品轻重时，所要称的次数比知道次品轻重时要多1次。在知道次品轻重总量n=4时，要称2次，这就意味着在不知次品轻重时，按猜想需要称3次，现在称2次就能找出次品。

（二）新的猜想

是原来的推论错误，还是不知次品轻重时，首次增加称的次数的总量与原来的不一样？接下来的这节拓展课，我们调整方向，再次展开了猜测与验证。当总量n=4时，不增加称的次数，那么当总量n=10，28，82……即n=3a+1时，是不是也不增加称的次数呢？

当n=9+1时，10（3A，3B，4C）称第1次，如果天平平衡，则次品在4个C中，4个待测物上面已经证明加称2次能找到次品；如果天平不平衡（假设3A重于3B），则证明外面的4个C是正品，可作为参考量，用（3A，3C）称第2次，若天平平衡，说明次品在“3B”中，并且次品是轻于正品的，所以再加称1次就能找到次品，若天平不平衡，则次品在“3A”中，并且次品重于正品，也只要加称1次就能找到次品。所以，当n=10时，与n=9所需称的次数一样都是3次，也不增加称的次数。

如果n=28，82，244……这些数都不增加称的次数，那么只要修改一下上一节课的推论，就可形成新的猜想。于是学生进行了新一轮的验证。果然，当总量n=3a+1时，都没有增加称的次数。

例如n=27+1时，28（9A，9B，10C）称第1次，如果天平平衡，则次品在“10C”中，上面已经证明10个的待测数量中找次品需要加称3次；如果天平不平衡（假设9A重于9B），则外面的10个C为正品，可用（9A，9C）称第2次，若平衡，则次品在“9B”中，并且次品轻于正品，需要加称2次就能找到正品，若不平衡，则次品在“9A”中，并且次品重于正品，也只需要加称2次就能找到正品。所以n=28时也不增加称的次数。接下来n=82，244等数都一一得到了验证。

（三）完善模型

于是，笔者又提出一个思考：总量n=3a+2，找次品时会不会也不增加称的次数？

当n=3+2时，不再是称2次，而需要称3次，也就是说要增加称的次数了。如，5（2A，2B，1C）称第1次，如果天平平衡，次品是C；如果天平不平衡（假设2A重于2B），则C是正品，次品在“2A”或者“2B”中，由于正品只有C一个，作为标准量嫌少，所以在4个次品中要找出正品，还需要称2次。

而n=9+2时，居然不需要增加称的次数。11（3A，3B，5C）称 第 1 次 ，如 果 天 平 平 衡，次品在“5C”中。这时再用（3A，3C）称第2次，如果平衡，则次品在外面的C4或C5中，这时只要用1个正品与之再称1次就能找到次品。即（A，C4）若平衡，次品是C5，若不平衡，次品是C4；若称第2次不平衡，则次品在“3C”中，并且已经知道了次品到底是重于3A还是轻于3A，所以也只要加称1次就能找到次品。

接着，n=27+2，n=81+2，n=243+2一一得到了证实，都没有增加称的次数，于是学生将n=3+2需要增加称的次数作为一个特例，允许出现这一点小“瑕疵”，并由此推导出：在不知次品轻重总量为3的乘方数时，找出次品的次数，正好比知次品轻重时加称1次，并且当总量为3的乘方数+1、+2的情况下，此“公式”也成立（特殊情况：n=3+1称的次数不变，但n=3+2就会增加称的次数）。

那么，最后一步，只要证明总量n=3a+3时，找出次品称的次数也会增加，我们的“找次品新模型”就能建立起来了。这一点大家还是有信心的，因为根据“三分法”，当出现+3时，三分后的每一份都增加了1。

三、第三次归纳猜想，重新构模

第三节数学拓展课，大部分学生都想要证明n=12时，确实增加了称的次数，需要称4次才能找出次品的时候，一位学生却拿出了n=12时不增加称的次数，也只要称3次的称法。

（一）第二次猜想也不对

当n=9+3时，12（4A，4B，4C）称第1次，如果天平平衡，则次品在“4C”里，还需要加称2次就能找到正品。因此只需要称3次就能找到次品。

如果A1B1C轻于A2B2B3，则次品有可能是B1（轻）或者是A2（重），然后第3次只要找一个正品来称一下（A2，C），也能称3次就找到次品。

这样一来，学生辛苦建立起来的模型又被打破了。因为接下来需要猜想和验证的可能性就更多了，比如27+3，81+3这些3的乘方数+3，是不是都不增加称的次数？然后+4呢？会不会也不增加称的次数？

（二）埋下一颗归纳探究的种子

研究到这一步，已经很难带领学生在课堂上以一课一个专题的模式进行探究了。笔者认为这样的尝试已经完成了课堂预期的目的：我们从一个不知次品轻重的题目进行探究，猜想出它的解答模型，随着探究的深入，发现模型有误，再重新调整我们的猜想并且通过数据去完善我们的新猜想。虽然最后我们臆想中的模型没有得到证实，再研究下去，对于小学生来说过于烦琐，但我们最后又有了更多新的猜想：

会不会关键总量在4，12，36……因为n=4的时候，跟3相比不增加称的次数，而12的时候，与9相比也不增加称的次数，而4和12正好是12（4，4，4）的关系。由此可不可以推论出 36（12，12，12）跟27相比，也不增加称的次数？

会不会是3+1，9+3，27+6，81+9……会不会是3+1，9+3，27+9，81+27……

笔者认为，真正的模型是什么并不重要，重要的是能在学生的心里埋下一颗种子，一颗敢于猜想、勇于试错的创新的种子。这才是比发现一个已知的数学模型更宝贵的财富。