学生解决鸡兔同笼问题的协变思维

□ 郜舒竹

如今的课堂教学倡导以学习活动为中心，当学生主动性充分发挥的时候，就会产生诸多教师难以预料的生成。如何面对并应对学生多样的生成，就成为教师现实的挑战。一个基本观点是：向学生学习，读懂学生做法中隐藏着的想法，将其提升为有价值的课程资源，应用于学生学习活动的设计。

一、协变思维

协变思维也可以叫作协变推理（Covariational Reasoning），指的是针对两个或多个协同变化的变量，进行协调或转化的思维形式。[1]比如“人多力量大”这一说法，针对“人数”和“力量”两个量，认为二者协同变化的规律是“人数越多，力量越大”，是一种“越多—越大（More—More）”的协变思维。

数学学习中，协变思维的应用非常普遍。比如，在问题情境中出现若干只鸡，对于鸡头数和鸡脚数两个量，其协变关系可以表述为“鸡头数的2倍等于鸡脚数”；同样，如果有若干只兔，那么兔头数和兔脚数的协变关系就是“兔头数的4倍等于兔脚数”。

更为复杂的情况是情境中出现更多的变量。比如鸡兔同笼，若干只鸡和若干只兔在一起，这时就出现兔头数、兔脚数、总头数、总脚数四个变量。某变量的变化或转换，会引起多个变量的变与不变。如果增加3只鸡，那么总头数增加3，同时总脚数增加6。将1只鸡换为1只兔，总头数不变，总脚数增加2。如果将2只鸡换为1只兔，那么总脚数不变，总头数减少1。

我国小学和初中数学课程中的鸡兔同笼问题，是我国历史上流传至今的名题。概括地说，解决问题的做法主要是《孙子算经》中的“半足术”，明代《算法统宗》中的“倍头法”，以及现在初中阶段的方程。

如果将鸡兔同笼问题叙述为：若干只鸡和若干只兔在同一个笼子中，总头数为35，总脚数为94。求鸡和兔各有多少只？

“半足术”做法的第一步是94÷2=47，相当于把鸡变为“独脚鸡”，兔变为“双足兔”，使得每只鸡的脚数和头数相同。这样47－35=12，就得到兔的只数。“倍头法”做法的第一步是35×2=70或35×4=140，就是将每只动物的头数变为2或4，与鸡或兔的脚数相同，便于进一步解决问题。[2]

下面介绍三种在四年级和五年级课堂中发现的学生做法，这些做法中蕴含着丰富的与协变思维相关的“大想法（Big Idea）”。

二、盈亏互补

课堂观察中发现学生的一种做法的第一步是，用总头数35去平均分配总脚数94（见图1）。

图1学生做法1

其中第一步算式为：94÷35=2……24，可以理解为，用35个头平均分配94只脚，也就是如果每只动物2只脚，就会多余24只脚。换言之，如果35只动物都是鸡，就多余24只脚。因此需要在总头数不变的情况下，总脚数增加24。

因为1只鸡变为1只兔，头数不变，脚数增加2。因此图1做法中的第二步24÷2=12，就是将12只鸡换为12只兔，使得头数不变，脚数增加24。因此共有12只兔。第三步35-12=23（图1中学生笔误：34应为35），求得鸡只数为23。类似于此的做法还有写为分数形式（见图2）。

图2学生做法2

这种做法背后隐藏的想法，既不同于《孙子算经》中的半足术，也不同于《算法统宗》中的倍头法。半足术与倍头法都是意图将动物的头数与脚数变为相同，也就是“变异为同”。而学生这样的做法首先是“平均分配”，分配之后，再对剩余部分进行调整。其中调整的过程所运用的，就是协调鸡只数与兔只数相互转换中变与不变的协变思维。

协调变量协变过程中的变与不变，也可以叫作“盈亏互补（Compensation）”，是一种应用广泛、具有一般意义的思维形式。比如下面的几何问题：

图3的大正方形内部有三个形状、大小完全一样而颜色不同的小正方形，露在外面部分的面积如图所示。求大正方形的面积。

图3 正方形问题示意图

初看题目，似乎无从下手。可以运用协变思维，将黄色正方形向左侧平移，移动过程中，黄色正方形露出面积越来越小，而绿色正方形露出面积越来越大，减少部分与增加部分保持相等，二者盈亏互补。移到尽头后成为图4形状。

图4正方形问题变形示意图

这时黄色和绿色两个正方形露出面积相等，由于移动过程中两个正方形露出部分面积相互之间盈亏互补，其总和是不变的。所以图4中黄色和绿色正方形露出部分面积均为(14+10)÷2=12。在此基础上，问题就不难解决了。

像这样从解题的具体做法中提取出具有一般意义的想法，西方文献中通常叫作“大想法（Big Idea）”。大想法的一个特征就是可迁移，可以应用于更广泛的其他问题。

三、配对分组

课堂观察中发现的第二种做法是将1只鸡和1只兔绑定为一组，使得每一组中包含1只鸡和1只兔，因此头数为2，脚数为6（见图5）。

图5 学生做法3

第一步94÷6=15……4，是用总脚数94除以每组脚数6，说明一共有15组，多余4只脚。也就是如果鸡和兔各有15只，这时就会多出4只脚。

第二步4÷2=2，是将剩余的4只脚分配给2只鸡，此时就有15只兔、17只鸡，总头数是30+2=32。

第三步35-(30+2)=3，表明总头数少了3。如果用1只兔换为2只鸡，能够使得头数增加1，脚数不变。

第四步15－3=12和第五步3×2+15+2=23，就是将15只兔中的3只，变为3×2=6只鸡。因此得到兔有12只，鸡有23只。图5最后一步23+12=35，是对结果的检验。

这一做法运用配对分组（Grouping）的想法，将1只鸡和1只兔视为一个整体，而后再对剩余部分进行调整，调整的过程同样用到盈亏互补的大想法。

配对分组不仅是一种解决问题的做法，也是可以迁移到其他问题，具有一般意义的大想法。比如下面著名的“百僧问题”。

100个和尚吃100个馒头，大和尚1人吃3个，小和尚3人吃1个。问大和尚和小和尚各有多少人？

运用分组的想法，将1个大和尚和3个小和尚视为一组，这样每一组中大和尚1人，小和尚3人，一共4人，吃馒头4个。这样就将100个和尚和100个馒头分为25组。因此得到答案：大和尚25人，小和尚75人。

配对分组作为一种思维形式，实质是将不同对象关联起来，视为整体。运用不同对象之间的异同、因果关系进行思考。比如美国20世纪著名的数学科普作家马丁·加德纳（Martin Gardner:1914-2010），曾经发表过一个命名为“Corner to Corner（点对点）”的几何问题。

圆内一个长方形，求长方形对角线l的长度。[3]

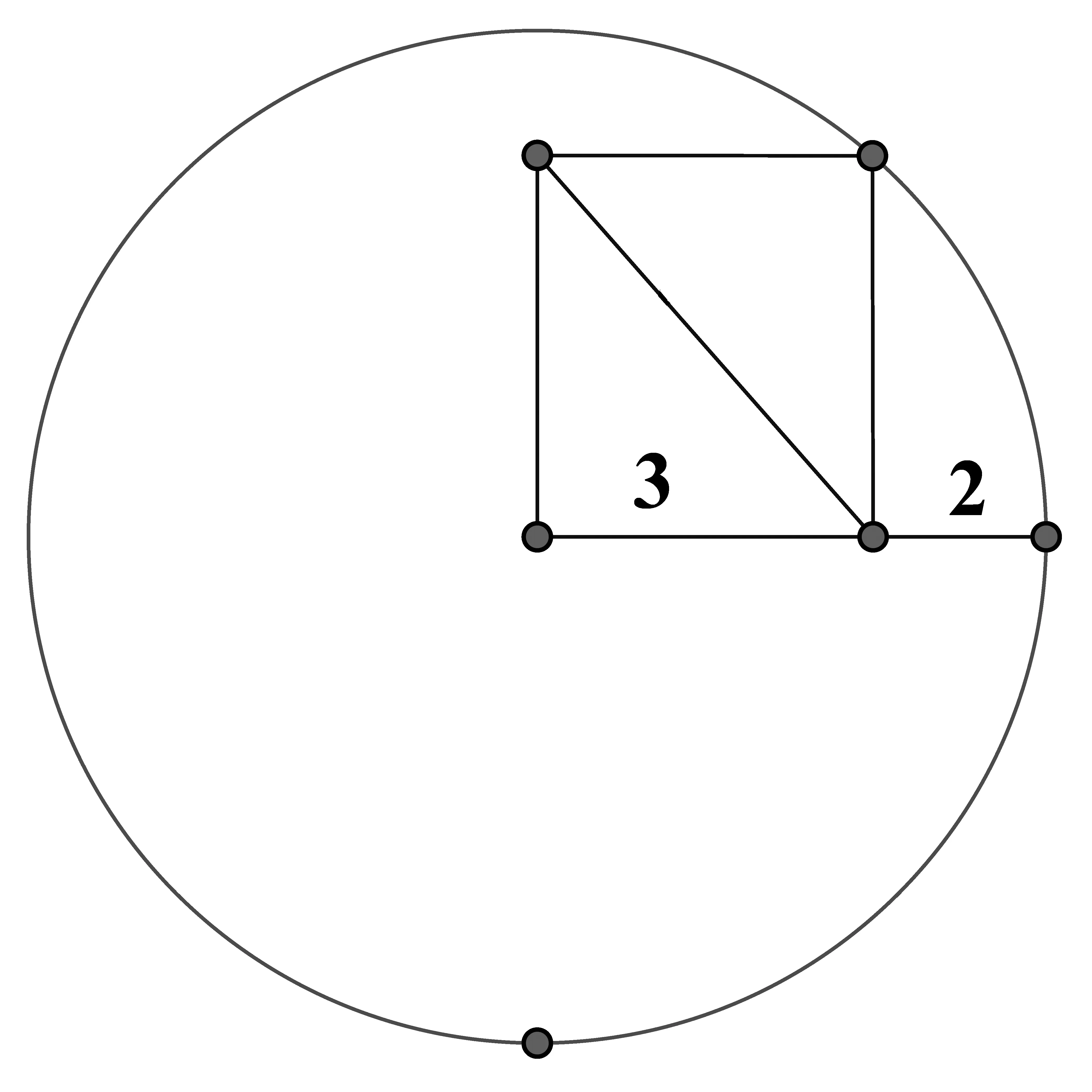
图6 圆内长方形示意图

如果眼睛只盯着图中对角线l，就无法将其与已知数据3和2建立联系。运用配对的想法，长方形有两条对角线，而且长度相等，可以发现另外一条对角线其实就是圆的半径，因此立刻知道对角线l的长度其实就是圆的半径长度：3＋2＝5。

四、先取半，再调整

观察中还发现，有学生做法的第一步是用总头数35除以2（见图7），相当于先假定鸡只数为17，兔只数为18；或者反过来鸡只数为18，兔只数为17。

图7 学生做法4

这样的做法可以概括为“先取半，再调整”。同样运用了鸡和兔相互转换的协变思维。如果鸡只数是17，兔只数为18，那么总脚数为17×2+18×4=106，比实际总脚数多了106－94=12。只需要将6只兔换为6只鸡，使得总头数不变，总脚数减少12。因此鸡只数为17+6=23，兔只数为18－6=12。这种“先取半，再调整”的做法也蕴含着可迁移、具有一般意义的大想法。比如下面的“和差问题”。

全班共有35名学生，男生比女生多3人。男、女生各有多少人？

通常的做法是通过“和加差”或者“和减差”解决问题。如果按照“先取半，再调整”的想法，第一步可以先将全班35人取半，具体做法为：35÷2=17.5。相当于假定男女学生各有17.5人。这种不符合实际的情境并不真实，因为不可能出现“0.5人”的情况。

心理学中有一个叫作“意象（Mental Imagery）”的概念，指的是“心眼所见（Seeing in the mind’s eye）”的情境[4]，这样的情境往往有悖于亲眼所见的“真相”。在和差问题的思考过程中，“0.5人”的意象，作为思考过程中的一个环节，虽然违背真实，但对于问题解决的思考仍然是有效的。

接下来，将意象中的“17.5个女生”中的“1.5个女生”改变为“1.5个男生”，这时总人数守恒不变，男生人数增加为17.5＋1.5＝19（人），女生人数减少为17.5－1.5＝16（人），符合题目中男生比女生多3人的要求，也就得到了问题的答案。

“取半（Halving）”作为一种分配活动中的大观念，其应用十分广泛。《孙子算经》中对鸡兔同笼问题解决所采用的半足术，就是对总脚数94取半。与其相关的大想法还有“加倍（Doubling）”和“等分（Equivalence Grouping）”等，比如《算法统宗》中的“倍头法”就用到了“加倍”。前面谈及的“配对分组”实际上也是等分想法的体现。

日常的数学教学中，解题是必不可少的教学活动，教师多多留意并积累学生异样的做法，从中挖掘具有一般意义的大想法，将之应用于其他问题的解决，应当成为教师自身专业发展的有效途径。

如今的数学教学倡导“变教为学”，期望以教师“讲为主”的教学，改变为以学生“学为主”的教学。对于教师的一个挑战是如何面对学生不同于预设的生成。这样的生成可能是正确的，可能是错误的，也可能是合理但不完善的。所有应对策略的前提是：耐心地听，努力地读，广泛地用。