经历“具体”到“抽象”，理解“确定”至“可变”——“用字母表示数”教学实践与思考

□ 金秀叶

【课前思考】

“用字母表示数”是人教版五年级上册第五单元“简易方程”的起始课，它是学生后续学习代数知识的基础。第一学段中，学生接触过用“图形符号表示特定量”的内容，如（）、□、○等，初步积累了用符号表示数的经验；第二学段开始学习用含有字母的式子表示数量关系。本课是“用字母表示数”的第一课时，让学生经历用字母表示数的过程，学会用字母表示一个量和数量关系，体会用字母表示数的必要性和简洁性。如何帮助学生从“具体”到“抽象”，理解从“确定”到“可变”，是本节课要重点思考并着力解决的关键问题。初学用字母表示数，学生会因不习惯而感到困难，应让学生体会到位，因而本节课主要体现以下几条主线：（1）抓住学生起点，从“记数”到用字母表示“未知数”。整个教学过程，从具体、确定的数到未知、不确定的数，理解用字母表示数的意义，体会用字母表示数的优越性。（2）在同一情境中，不同的字母表示不同的数。（3）在同一情境中，明确两个量之间存在相差或倍比关系时，在用一个字母表示某个量的前提下，可以用字母关系式来表示另一个量。（4）引发学生冲突，从“量”到“数量关系”，用含有字母的式子表示关系。本课中让学生对“b”和“a＋5”进行思辨，根据两个量之间的关系，初步理解用含有字母的式子能表示数的含义，让学生经历“引发冲突、修正概念、完善概念”的过程。（5）用三个红包的钱数，分别为a元、（a＋5）元、2a元，让学生提出问题，将学生提出的问题转化成教学资源，以突破教学难点。

【教学目标】

1.在具体情境中理解用字母表示数的意义，初步认识用字母表示数的作用，能够根据具体情境用含有字母的式子表示数量关系和一个量。

2.经历将实际问题用含有字母的式子进行表达的必要性和过程，体会用字母表示数的概括性与简洁性，提高抽象概括能力。

3.发展符号意识，感悟用字母表示数的思想，培养创新意识。

【教学重难点】

1.理解并掌握用字母表示数的方法，体会用字母表示数的优越性。

2.用含有字母的式子表示数量关系和一个量。

【教学过程】

一、直接解读，探究发现

图1

1.尝试表示，引入字母（1）体会确定数

师：生活中我们经常会收发红包，前几天我就发过一个红包，看懂了吗？（出示微信红包图，如图1）请你把它记录在练习纸上。

（生独立记录，师板书：18元）

（2）体会用字母表示数的意义

师：（笑）红包一发出去啊，我也会收到红包。这是我收到的第1个红包（如图2）。多少元？会写吗？

（生皱眉、摇头）

师：碰到什么困难了？还没点开哦！那你们猜猜看是多少元。

生：12元、18元……师：能再大点吗？

图2

生：150元、200元、500元……

生：我觉得不可能是500元，因为我知道现在发微信红包一次不能超过200元。

师：微信红包一次最大多少元？最小呢？生：最少发0.01元，最多不能超过200元。

问题驱动：0.01～200元只是一个范围，这里面有许多数，你能用什么方法来表示这个范围里面的任意一个数吗？自己在练习纸上试一试！

（设计意图：刚开始学生容易纠结于红包的范围，大部分都用0.01～200元表示，后来改变提问，告诉学生0.01～200元是一个范围，里面有许多的数，引导学生想办法表示出这个范围内的任意一个数，学生想到了用“？”、图形以及字母来表示这个数。）

生：1～18。

师：表示出所有的可能了吗？

生：用？、△。

师：你是怎么想的？哦，你认为它是未知的。生：x元。生：a元。

师：有同学用符号或图形来表示，也有同学用字母表示。同学们，对于一个未知的数量，数学家们也想表示，你们猜最后用的是什么方法？

（课件出示资料：韦达（1540—1603），法国数学家，是第一个系统使用字母来表示数的人，被誉为“代数学之父”。）

师：同学们，你们真是太厉害了，知道用字母来表示一个数，今天这节课我们就一起来学习“用字母表示数”。

（设计意图：使学生深刻理解未知的量，体会用字母可以表示不确定的、未知的数，这是本节课的首要目标，即一元认知水平。）

师：好，刚才的x、a……用这些字母代表未知的数，都是可以的。那现在我们统一用a元来表示第一个红包的钱数。你表示好了吗？（板书：a元）

（3）思辨已知与未知

师：刚刚我们分别用“18”和“a”表示红包的钱数，有什么不同呢？

生：18是一个已知的数（板书：已知），a是一个未知的数（板书：未知）。

（4）感受多元性

师：收到的第2个红包，还没点开，多少元呢，能把它表示出来吗？a元？b元？……

师：可以吗？这些字母都表示了未知的数，你觉得哪个更好？

师：是啊，字母不同，代表的数也不同，那第2个红包我们就用b元来表示吧。

2.走进代数，感受思想

（1）关注联系，引发思辨

师：第2个红包比第1个红包多5元，可以怎么表示呢？

师：（a+5）元，都这么表示的吗？怎么想的？（呈现b和a+5）

师：之前我们用b元表示了第2个红包的钱数，增加一个信息后用了（a+5）元来表示，你觉得哪个更好呢？

生：（a+5）元更好，因为它比b元更具体。

师：什么叫更具体？

生：（a+5）元表明和第1个红包是有关系的。

生：（a+5）元还能表示第2个红包比第1个红包多5元。

师：是啊，b元是可以的，但（a+5）元不仅可以表示出第2个红包的钱数，而且可以看出第2个红包比第1个多5元的关系。好，现在我们已经很清楚了，第2个红包的钱数就可以用（a＋5）元来表示。

（设计意图：通过对“b”和“a＋5”进行思辨，关注两个量之间的关系，让学生经历用含有字母的式子表示数的抽象过程，这是本节课的难点——字母可以参与运算。）

师：第3个红包是第1个红包的2倍，怎么表示第3个红包呢？

（生在黑板上写下a×2）

师：怎么想的？

生：a的2倍，就用a×2表示。

师：原来它和第1个红包也是有关系的。在写含有字母的式子时，数和字母相乘的时候，一般要把数写在字母前面，乘号可以省略，如n×6＝6n，所以a×2=2a，你们也可以写写看。

（2）提出问题，解决问题

师：现在根据这3个红包的信息，你能提出什么数学问题吗？

（同桌讨论，反馈交流）

①第1个红包和第2个红包一共多少元？

生：a＋a＋5＝（2a＋5）元。

②第2个红包和第3个红包一共多少元？

生：a＋5＋2a=（3a＋5）元。

③那这3个红包一共多少元？

（师投影学生作业：a＋a＋5＋2a）

师：一共是多少呢？

生：（4a＋5）元。

师：要知道3个红包一共多少元，只要知道第几个红包就可以了？

师板书：当a＝10时，

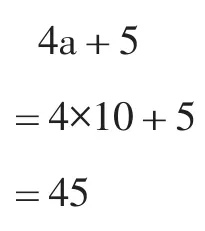
④第3个红包比第2个红包多几元？

师：相差多少我们以前是用什么方法解决的？

生：减法。

师：现在你会列式吗？

生：2a－（a+5）。

⑤哪个红包最大？

师：那到底哪个红包最大呢？

生：我觉得第3个红包最大，比如a=6元，第2个红包是11元，第3个红包是12元。

生：也可能是第2个红包最大，a=1元，第2个红包是6元，第3个红包是2元。

师：居然被你反转了，太不可思议了！

生：我觉得也可能是相等的。

师：什么意思？

生：如果a=5元，第2个红包是10元，第3个红包也是10元。

（掌声响起，学生脸上表现出不可思议的表情）

师：用字母表示数也是可以比大小的，看来这是一个好问题，学数学就应该学会问问题。

（设计意图：根据学生提出的问题组织教学，学生在交流活动中，呈现自己的想法，用字母表示数时要比较大小，在碰撞中课堂不断反转，实现了从“算术思维”到“代数思维”的转变。）

（3）课堂小结

师：今天我们学了“用字母表示数”，学了这节课后你有什么想法？

生：用字母可以表示未知的数。

生：我感觉字母很神奇……

二、巩固练习，加深理解

1.创设情境，加深理解

根据剪下的长方形纸条的长度计算面积，完成下表。

长度/cm面积/cm2 5 6 9 15 ……

（1）体会简洁性

师：求面积你们是怎样列式的？

生：长×宽。

思考：“……”在这里表示什么呢？你能把所有的情况都表示出来吗？

（2）联想意义

师：在这里，“4a”表示这个长方形的面积。“4a”在不同的情境中可以表示不同的含义。比如：一辆汽车每小时行a千米，4小时行的路程就用“4a”千米来表示。你觉得“4a”在生活中还可以表示什么呢？把你的想法在四人小组里交流一下。

生：每千克苹果a元，4千克苹果4a元。

生：每分钟写a个字，4分钟写4a个字。

生：如果正方形的边长为a，周长就表示为4a。

……

师：你们都很会思考，看来4a在生活中可以表示很多实际含义。

（设计意图：对“4a”这一式子可以表示的实际含义进行多样化的解读，让学生经历从一般到特殊的过程，体验字母表示数的价值，理解含有字母的式子所表示的数量关系。）

2.独立探究，感悟关系

师：请你在纸上写出三个连续的自然数。

（生独立完成后教师组织交流反馈）

生：4，5，6。

生：100，101，102。

师：检查相邻两数相差多少。你能用字母表示出来吗？

生：a，b，c。

生：x，x+1，x+2。

生：a，b，c是不可以的，因为a，b，c不一定相差1，这只是英文字母中的顺序。

生：x，x+1，x+2，这个可以，因为相邻两个数都相差1。

师：刚才我们是把第1个数表示为x，那如果我们把第2个数表示为x，那另外两个数怎么表示呢？（板书：x－1，x，x+1）想一想：这两种方法不变的是什么？

（设计意图：进一步体会用字母表示数的简洁性，加深对数量关系的理解，感悟代数的神奇。）

师：同学们，无论字母是表示第1个数还是第2个数，只要能表示出这三个数之间的关系都是可以的。看来字母真的很神奇，它能以不变应万变，相信大家在以后的学习中会有更多的发现。

【课后思考】

好学的天性促使学生在本节课中不断地根据信息发现问题、提出问题。课始，以问题引领，引发学生思辨：“0.01～200元只是一个范围，这里面有许多个数，你能用什么方法来表示这个范围里面任意的一个数？”学生想到用“？”或符号来表示，再想到用字母表示数，层层深入，感悟符号表示的思想。接着，学生根据数量关系用含有字母的式子表示第2个红包和第3个红包的钱数，又根据这三个红包之间的联系，积极思考提出问题，并产生解决它的欲望，形成了“问题意识”，特别是“第3个红包比第2个红包多几元”“哪个红包最大”这两个问题，让学生的思维向着纵向和横向不断延伸，学生在交流中很自然地想到用“代入求值”，从而感受到随着a取值的变化，a+5和2a的值也会发生变化。学生觉得用字母表示数真的很神奇。张奠宙先生说过“数学的价值在于运算”，对于用字母表示数，功夫要花在“字母参与运算”上，这一点在本节课中得到了落实。