夹逼法则解题例说
2019-10-14浙江省金华市第六中学321000
浙江省金华市第六中学 (321000)
虞 懿


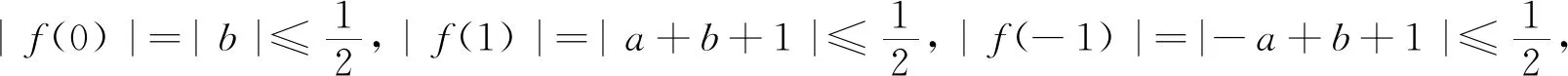

例2 定义在R上的函数f(x),均有
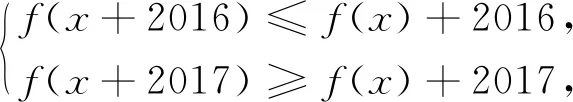
解析:由f(x)+2017≤f(x+2017)=f(x+1+2016)≤f(x+1)+2016,所以f(x+1)≥f(x)+1①,又利用①式得f(x)+2016≥f(x+2016)=f(x+2015+1)≥f(x+2015)+1=f(x+2014+1)+1≥f(x+2014)+2≥…≥f(x+1)+2015,所以f(x+1)≤f(x)+1②,由①、②得f(x+1)=f(x)+1,从而an+1-an=1,所以a2018=a1+(2018-1)×1=2019.
评注:本题由递推关系,通过迭代得到f(x+1)≥f(x)+1且f(x+1)≤f(x)+1,再利用“夹逼法则”将不等式转化为等式.
例3 若实数x,y满足2x-3≤ln(x+y+1)+ln(x-y-2),则xy=.

评注:借助不等式lnx≤x-1(x>0)是顺利求解本题的关键.




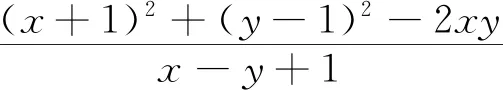
例5a,b为实数,不等式|x2+ax+b|≤|x2-7x+12|对一切实数x都成立,则a+b=.
解析:因为x2-7x+12=(x-3)(x-4),所以在|x2+ax+b|≤|x2-7x+12|中,令x=3与x=4得9+3a+b=0和16+4a+b=0,解得a=-7,b=12,所以a+b=5.
评注:题中有两个参数,但只有一个绝对值不等式,要求我们求出参数的值,这似乎有点“山重水复疑无路”.但通过合理赋值可得不等式|9+3a+b|≤0与|16+4a+b|≤0,这样就夹出了两个方程9+3a+b=0和16+4a+b=0,真可谓“柳暗花明又一村”.

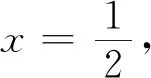
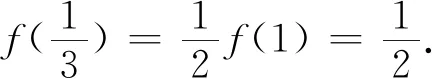
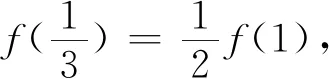

“夹逼法则”体现了数学的对称美,借助夹逼法则解题,方法精巧,思路独特.不等与相等是既对立又统一的两个概念,“夹逼法则”有力地将它们统一起来,从而有效地将不等关系转化为相等关系,使一些看似复杂的问题迎刃而解.
