一道高考题的多角度研究
2019-10-14江苏省扬州中学225009
中学数学研究(江西) 2019年10期
江苏省扬州中学 (225009)
王 晨 戚有建
很多高考题看起来很平常,实际上却丰富多彩,都是专家经过精心思考编制出来的,所以有很大的教学价值和研究空间.本文从一道高考解几题出发,首先对问题进行了推广研究、类比研究,然后研究问题的背景,最后研究背景的应用.
一、考题展示
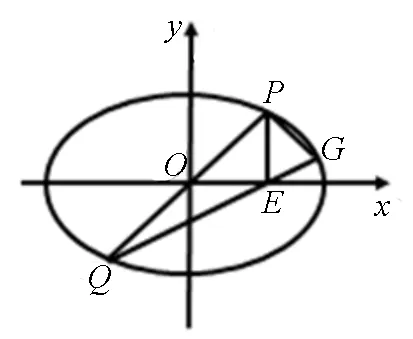
图1
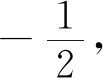
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交曲线C于点G,证明:ΔPQG是直角三角形.
点评:本题是2019年全国卷Ⅱ理科数学的21题、是选拔题,与2011年江苏卷18题相似度很高.第(1)问考查轨迹方程,用直译法处理即可,注意椭圆不含左右顶点;第(2)问考查用方程来研究曲线的性质,即用代数方法(坐标法)来研究几何问题(垂直问题).本题看起来很平凡,实际上却平而不凡,有很大的研究价值,我们重点研究第(2)问.
二、解法研究
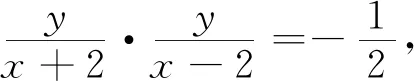




解法2以点P,G的坐标x1,y1,x2,y2为参数,通过代数运算(坐标运算)来解决几何问题(垂直问题),借助点差法、设而不求,充分体现了解析几何的基本思想,但由于解题过程中涉及四个参数x1,y1,x2,y2,所以消参时有一定困难,对代数变形的要求较高.
三、推广研究

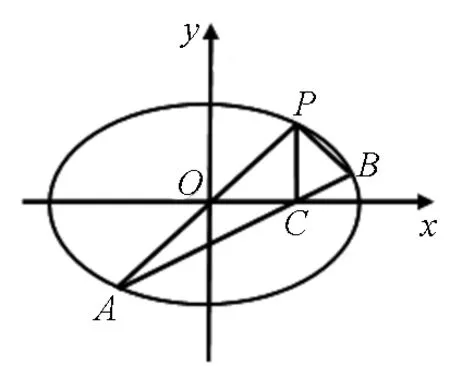
图2

四、类比研究
将命题1类比到双曲线中,可得下面命题:

五、背景研究

图3

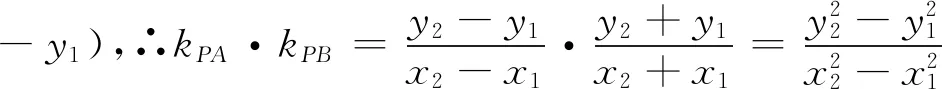



六、相关推论
实际上从命题3出发可以得到很多推论:

图4

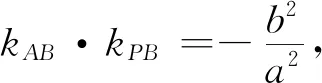

七、背景应用




图5