基于核心素养理念下的新授课教学初探——以《平面向量的概念及表示》的几个教学片段为例

江苏省溧水高级中学 (211200)

李国林

1.问题提出

《普通高中数学课程标准》修订组认为，数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算与数据分析六个维度.可见“核心素养”是新一轮基础教育课程改革的基础，教学是让核心素养落在实处的关键，思维又是教学的核心.在课堂中如何既实现的教学目标，又让核心素养潜移默化的植根在学生心里，成为我们教师新的学习方向.近阶段，本人受邀在一所四星级高中上一节示范课，笔者在课堂上作了一些变化，既完成了教学目标，也尝试将数学的核心素养融入课堂中.不当之处，请批评指正.

2.学情分析

平面向量作为三角函数与三角恒等变换之间的一个章节，显然对三角函数的研究起着非常重要的作用，它是证明两角和差公式的最有效的工具，也是后期研究三角形等相关问题的重要工具，同时作为独立的章节，又有其独特性，它本身既具备“形”的特征——方向，又具备“数”的体征——长度，所以本节课作为该章节的起始课应让学生体验概念的产生的过程，让学生理解概念的本质，构建概念的体系.进而从不同的维度认知新概念，潜移默化的渗透核心素养.

3.设计与教学

片段一:创设情境，引入新概念，提高学生的数学抽象能力.

问题1：大家都出去旅游过，从景点A到景点B的路程和位移是一样的吗？

生(众)：不一样，路程只有大小，位移既有大小还有方向.

问题2：很好，我们接触到了一个新“概念”，那么大家在生活中还有这样的例子吗？

生1：有，物理中学习的力，速度，加速度.

问题3：我们数学是一个巨人，物理是站在我们数学的肩膀上的伟人，今天我们要在数学的内部研究这个新“概念”.请大家告诉我这个新“概念”必须具有哪些属性呢？

生(众)：大小和方向.

设计意图：对于新授课，很多老师会直接给出概念，让学生死记硬背，再加以大量练习，让学生熟练，这样的熟练效果是暂时的；概念教学首先要解决的问题是为什么要学习这个内容，皮亚杰提出认知冲突理论：即学生在具备一定水平的认知结构上，常常对输入新的信息采取同化的方式，而当不能同化时，已经同化与企图同化的信息之间就有了矛盾，导致认知结构内部的不平衡，从而能使学生的求知欲由潜伏状态转化为激活状态，从而开启学生的思维大门，这样也就找到了新旧知识的衔接点.

本课借助学生已有的物理知识，让学生知道在我们的生活中是有这样“量”包含了“大小与方向”，但在这个时候我没有直接给出概念，而是学生发现这样的“量”在我们数学中还没有过，我们需要一个新的知识来解决这个“量”，进而让学生先总结它们的属性，这样既让学生明白新概念应确实需要具备哪些属性，更让学生经历了概念发现的过程，培育了学生的理性精神.

片段二：激发兴趣，小组合作，探究问题，完成学生数学建模的过程，发挥学生的直观想象.

问题4：我们在数学中把这个概念称为“向量”，下面请大家小组讨论，知道了向量的概念后，我们该研究它的什么属性呢？

(有的小组讨论很多，有的小组比较模糊，我又作了引导，我们在中小学阶段学习线段、射线、直线概念之后研究它的属性是怎么作图表示，怎么数学符号表述)

生2：它在代数上及在图形上的表示.

问题5：请大家在网格纸中画一些向量，并先在小组中说说它们的属性？

生3：我们组画出了一些特殊向量：单位向量、零向量.

生4：我们组还发现两个向量之间有大小相同的和不同的，方向相同和相反的.

设计意图：章建跃博士曾说过，教什么比怎么教更重要.授人以鱼，不如授人以渔，很多老师新概念出来之后就直接给出其特征，这样就让学生失去了自主构建的机会，学生在之前是有过这样的建构经验的，那么我们老师能不能在这里等一等，尝试唤醒学生的记忆，这样才能让学生“觉悟”.同时本节课知识有些零碎，很容易变成学生背诵，我们能否将“冰冷”的知识转化成“火热的发现”.通过让学生自己自由的画图，并总结出两向量间的关系，最后引导学生把相关的结论书写下来，引导学生经历观察、尝试、猜测、交流、推理、反思等思维过程，让学生学到知识的同时，亦培养了学生逻辑推理、数学抽象、直观想象等数学素养.

片段三：小组活动，让学生阅读课本，进行数据分析，完善已经学过的，查找新问题.

问题6：大家总结的很好，那么大家都发现完了吗？请大家阅读课本，明确我们刚刚所得到的概念，同时谈谈有什么疑惑，请提出问题？

(学生积极性再次高涨，纷纷想看看自己的总结是否完整)

生5：老师说向量表示应有箭头，但书上的小写字母表示却没有箭头.

生6：什么是自由向量？

生7：单位向量、零向量是什么方向呢？

生8：两个向量能不能相加？

师：非常好，这说明同学们是认真阅读，并用自己刚刚掌握的知识来进行辨别.有没有其他同学代替老师解答呢？

问题7：刚才提到单位向量和自由向量，如果我们平面中所有单位向量的起点都移到一起，那么它们的终点所形成的轨迹是什么呢？

生(众)：单位圆.

设计意图：明朝陈献章曾说过，前辈学贵有疑，小疑则小进，大疑则大进.疑者，觉悟之机也，一番觉悟，一番长进.在学生完成数学发现之后，他们已经初步具备了平面向量的基本概念，基本知识，让学生这时进行数据分析，更有利于学生利用所学知识来发现问题，学生此时对课本中文字语言、图形语言及符号语言进行相互转化就需要直观想象、数学建模、逻辑推理等核心素养相互作用，进而提高了学生的综合能力.让学生的知识储备得以螺旋式上升.

片段四：典型例题，巩固概念，提高学生逻辑推理能力.

例1 判断下列说法的真假，并说明理由

(1)平行向量的方向一定相同；

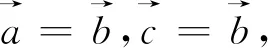
设计意图：逻辑推理与数学运算是数学教学活动的核心，也是培养科学素养的重要途径，有利于学生理解结论的来龙去脉，通过对例题的分析，加深学生对定义本质的理解，培养学生的反思习惯，有利于学生形成有论据、有条理、合乎逻辑的思维习惯和交流能力.

4.教学反思

4.1 着眼于新概念的形成过程，在学生参与知识建构过程中培养学生的核心素养.

《课标》指出：“高中数学课程应该返璞归真，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程.”因此在新授课的问题情景中，我们要在学生已有的知识基础上，充分调动学生的积极性和挖掘学生的潜能，老师仅仅作为引导者，给学生发现问题，提出问题的机会，让这样才能有利于学生的知识建构，并在建构过程中提高学生的数学抽象、逻辑推理、数学建模、直观想象、数学运算与数据分析等方面的核心素养.

4.2 着眼于数学问题的探究过程，让学生在自主探究中提高核心素养.

近年来，老师对核心素养总觉得“高大上”，不是自己能理解的，其实它是很平易近人的，随着课堂的进一步深入，它正在潜移默化的进村(课堂教学改革之村)入户(课堂实践之户)，只要我们老师能理解核心素养的特点，它随时都可以在我们的课堂中呈现.本课中通过向量的概念的研究让学生分阶段的自主的学习到了新知识，并对向量的“数”、“形”的特征都有了更深的认识，更让学生在探究中运用了观察、分析、归纳、推理、运算等技能，提升了学生的数学核心素养.

4.3 着眼于数学思想方法的渗透，让学生能潜移默化的接受方法，提升核心素养.

核心素养的培养是为了提高学生相应的能力，以适应个体发展和社会发展，所以它不是一个题，由老师直接给学生答案，它是一种习惯，要让学生在不知不觉中使用它.我们老师应根据本节课的特点，有目的的培养学生相应的核心素养，可以多也可以少，但不能没有，所以老师要在教学中给学生数据让其分析，给学生时间让其讨论，给学生学生问题让学生去解决，这样才能唤起学生的求知欲，提高学生的能力，提升了学生的数学核心素养.