探究性学习的问题设计与探究过程——以一次试卷讲评中的圆锥曲线探究性问题为例

湖北省恩施州教育科学研究院 (445000)

周 威

《普通高中数学课程标准(2017)》说到，数学探究活动是围绕某个具体的数学问题，开展自主探究、合作探究并最终解决问题的过程,重点提升学生数学抽象、数学运算、数据分析、逻辑推理和直观想象等核心素养，那么从历年高考对圆锥曲线中椭圆问题的考查来看，基本上就是一个自主探究过程，在解决问题过程中考查学生的数学核心素养，它融入了解析几何方面所有的数学基本思想、方法、技能，而且考查面基本稳定.因此本文中笔者以一道圆锥曲线高考模拟题为例，通过采用“问题—探究—结论”的探究过程，引导学生进行一系列的探究活动，最终得到此类圆锥曲线的一般性质.

(1)求椭圆C的标准方程；

(2)过P(1,0)作动直线l交椭圆C于A、B两点，Q为平面上一动点，直线QA,QB,QP的斜率分别为k1,k2,k0，且满足k1+k2=2k0，问Q是否在某定直线上运动，若存在求出该直线方程；若不存在，请说明理由.

本题第(1)问这是常规的封闭题型，历年高考考查稳定，主要考查基础知识、基本方法，体现对数学运算、逻辑推理等核心素养的考查.第(2)问属于开放题型，难度适中，它蕴含的内涵也是十分有趣的.需要选择合适的运算方法，强化探究运算思路.

1.纵向探究：由特殊到一般

问题1 从此题的解答过程和结果中的直线方程为x=4的来看与椭圆的要素a2,b2有关吗？

生1：在此题中a2=4,b2=2，应该与a2有关.

问题2 那么直线方程是不是就是x=a2呢，如果不是那么还与什么有关呢？

生2：从第(2)问中运算过程直线l方程：y=k(x-2))代入椭圆的计算过程来看，应该不是，应该与P(1,0)点有关.

生3：确切的说应该是与P(1,0)点中的横坐标有关！

生4：应该是a2乘以或者除以P点的横坐标。

师：很好！那么具体是怎么一种关系呢？

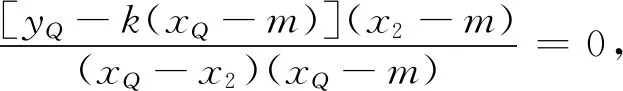
(2)当直线斜率不存在时，直线l垂直x轴，由对称关系知也符合题意.所以有如下性质：

师：通过刚刚的探究过程，对m的范围有什么限制吗？

生5：当m=0时，显然并不存在这样的定直线.另外，m的取值范围只要保证Δ=(2k2a2m)2-4a2(k2m2-b2)(a2k2+b2)=4a2b2[(a2-m2)k2+b2]>0即可，也就是说只要保证直线l与椭圆有两个交点，上面性质1是成立的.

师：是的！如果m取一些特殊值m=c,会是什么结论？

生6：若m=c时，P(c，0)就为椭圆右焦点，那么可以推出:

2.横向探究：迁移到其他圆锥曲线

探究过程2:(1)当直线斜率存在时，设直线l为：y=k(x-m)与双曲线交于A(x1,y1)、B(x2,y2).Q为(xQ,yQ),将直线代入双曲线方程得(b2-a2k2)x2+2k2a2mx-a2(k2m2+b2)=0，x1+x2=

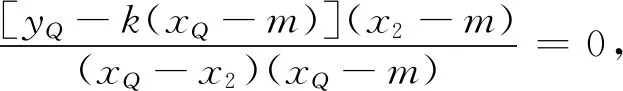
(2)当直线斜率不存在时，直线l垂直x轴，由对称关系知也符合题意.因此可以有如下性质：

师：很不错！刚刚探究速度快了不少，你们发现了什么规律吗？

生7：(得意洋洋)这和前面探究过程1的思路和步骤是一样的，我只是在上面改动了数据和符号！

问题5 若将一般双曲线改为一般抛物线的条件下，P点是x轴上除原点的任意动点，是否存在定直线方程？

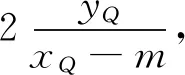
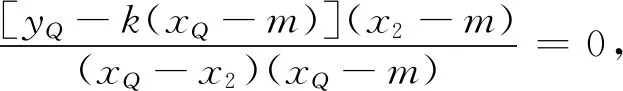
(2)当直线斜率不存在时，直线l垂直x轴，由对称关系知也符合题意.所以有:

性质3 已知抛物线y2=2px(p>0)，过动点P(m,0)(m≠0)作动直线l交抛物线C于A、B两点，Q为平面上一动点，直线QA,QB,QP的斜率分别为k1,k2,k0，且满足k1+k2=2k0，那么Q点横坐标为xQ=-m.

从探究结果来看，问题3、4、5都得到了很好的回答.值得一提的是，上述性质1、2、3，对焦点在y轴上的椭圆、双曲线、抛物线依然可以类比得到，这时我们可以采取先结论后证明的方法，这里不再赘述.

3.逆向探究：由结果推条件

(2)当直线斜率不存在时，直线l垂直x轴，由对称关系知也符合题意.所以有:

师：通过探究过程4，是否可以猜测对于双曲线，抛物线也有类似结论？

生8：是的，这是一个充要条件！

师：很好！请同学们自己完成相应性质5、性质6的表述，并证明.

至此，通过这些问题设计与探究过程，我们完成了篇首题目的探究与推广.通过对圆锥曲线一般性质的探究性学习，不仅仅是熟练技巧和方法，从证明过程中可以发现，对于研究圆锥曲线往往有“套路”，这种“套路”不是通过题海战术或者说多做几道题就能发现的，需要方法类比，需要知识迁移，学生才能从具体的数学情境中抽象出数学概念、命题、方法和体系，积累从具体到抽象的活动经验，才真正领悟这种“套路”当中的内涵，也只有这样才能把握事物的本质，才能有知识的生成，就如本文中得到的准线关于椭圆、抛物线、双曲线的性质，它对圆锥线具有相同的呈现方式，这也更让学生体会到圆锥曲线的神奇.这对激发学生学习数学的兴趣是大有裨益的，这样的探究活动在教学中也应必不可少.