高考数学解题“隐性失分”举隅与教学对策

□周如俊

（江苏省灌南中等专业学校，江苏灌南 222500）

数学考试中，考生失分的原因是多种多样的，但是一部分失分具有鲜明的共性——“隐性失分”，在平时学生学习与教师教学中却往往被忽视.所谓“隐性失分”是指解题策略上失误、思维定式、心理定式等非知识性因素造成的主要失分[1]，而且解题者有时难以自我诊断与发现.“隐性失分”在高考解题失分中所占的比例相当大，是影响高考数学成绩大范围提高的一个不可轻视的因素.本文以2019年江苏省高考数学试题为例，对考生常见“隐性失分”的原因加以分析，并提出相应的教学对策.

一、“会而不对”——“无”果的隐性失分

所谓“会而不对”，是指考生解答考题时，常受平时教学“巧解”（如“定义法”“特例法”等）刷题训练影响，先入为主，企图借助“巧法”“直捣黄龙”得分，结果陷入命题者设计的“解不出来”的“陷阱”之中，造成“会而不对”的“隐性”失分后果.

例1（2019年江苏高考第17题）如图1，在平面直角坐标系XOY中，椭圆1(a＞b＞0)的焦点为F1（-1，0），F2（1，0）．过F2作x轴的垂线l，在x轴的上方，l与圆F2:(x-1)2+y2=4a2交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1．已知

（1）求椭圆C的标准方程；

（2）求点E的坐标.

图1

【解析】本题主要考查考生推理论证能力、分析问题能力和运算求解能力.

（1）本题部分考生考完后说很“悲伤”，究其原因是“先入为主”造成的，试图想通过椭圆定义的“巧法”，结果陷入“会而不对”无法求解的误区.

设椭圆C的焦距为2c，则F1F2=2c=2，c=1.

可求得D点的坐标为即

因a2=b2+c2，即b2=a2-1，代入上式（*），化简整理得：

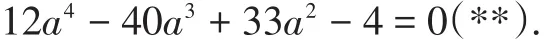
对于方程（**），部分考生因心理紧张，结果解不出来，导致第（2）解题也直接失败，还有部分考生说，将方程（**）左边因式分解，得：12a4-24a3-16a3+32a2+a2-4=0，即有：(a-2)(12a3-16a2+a+2)=0,a-2=0,a=2，但因纠缠于12a3-16a2+a+2=0（***）求解，花费大量时间却求不出（***）解来，又陷入后文所述“对而失时”——“繁”解的隐性失分误区.上述解法可能正是命题者设计的“请君入瓮”——定义法求解的“会而不对”的命题“陷阱”.

事实上，换个思路，解题“干净利落”，有“直捣黄龙”得分之效.

由b2=a2-c2，得b2=3.

因此，椭圆C的标准方程为

（2）解略

【教学对策】教学中（学习中）一味追求“巧解”，必然缺乏对数学基本思想方法的挖掘和相应的训练，从而冲淡和掩盖了对基本方法的渗透.一种严重影响就是当学生对于一类题目一旦了解或掌握了某一个巧解后，就对较为复杂的基本方法产生厌倦心理，也就从根本上阻碍了数学基本思想方法的渗透．综观近几年高考数学命题，考查考生数学综合运用能力，主要体现在数学思想与“通法”运用上，学生解答高考试题的问题还是出在对常规方法的掌握上．因此解题教学中要辩证地看待“通法”与“巧法”[2]，充分发挥通法和巧法各自的教学功能，不能“顾彼失此”：首先追求解题通法运用，然后通过“巧思妙想”渗透，寻求一种最美和最简捷的证明（解法），激发学生学好数学的兴趣，培养创新精神和创造能力．

二、“对而失时”——“繁”解的隐性失分

所谓“对而失时”，是指考生解答考题时，常因思维封闭、方法单一，只知道从命题条件顺水推舟，一“推”（算）到底，不善于改变思维角度，修正解题方向，以求得“最佳”方法，节省时间和精力，结果造成“小题大做，小题繁做”，浪费了其他大题解题时间，导致“全而不巧”费时式的隐性失分后果.

例2（2019年江苏高考第12题）如图2，在△ABC中，D是BC的中点，E在边AB上，BE=2EA，AD与CE交于点O.若，则的值是_________.

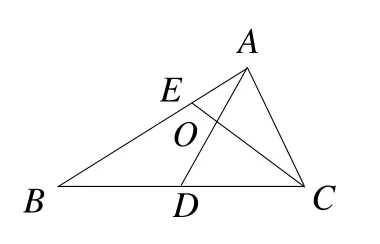
图2

【解析】本题考查在三角形中平面向量的数量积运算，渗透了直观想象、逻辑推理和数学运算素养.考生习惯运用“坐标运算法”求解，通过坐标法的处理，结合点的坐标、向量的坐标的转化，解决向量问题.

图3

解题第一步：坐标转化.如图3，建立直角坐标系，将几何问题转化为学生熟悉的有明确关系的距离公式运算：

解题第二步：关系探寻.探寻m，n关系，然后代入（*）求解.探寻向量与向量关系：通过向量加减运算，将向量转化为向量来表达．

由定比分点公式求得E点坐标为，则直线AD方程为，直线EC方程为联立直线AD，EC两方程，求得E点坐标为，即O是线段AD中点．

证明结论“O是线段AD中点”，除了上述“求直线交点法”外，考生有时还通过“向量法”小题大做证明：

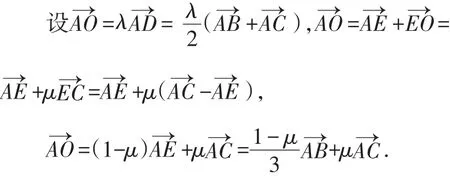
解题第三步：参数转换.探究m，n关系．由知：(-1-m，0-n)·(1-)，化简，整理得：n2=-m2+4m-1（**）．

上述解题第二步“关系探寻”中两种方法证明“O是线段AD中点”的结论，有点“小题大做，小题繁做”，陷入命题者设计的“对而失时”解题误区，耽误了其他试题解答的宝贵时间，导致“全而不巧”费时式的隐性失分.当然，部分考生“看不出”或证明不出“O是线段AD中点”的隐含结论，此题也就变成了学生解答的“拦路虎”，甚至学生花费了大量时间进行向量线性变换或坐标转换，也得不出正确答案，此时解题陷入了后文所述“隐而不发”——“难”解的隐性失分的误区.

其实，解题第二步“关系探寻”，还可以采用三角形中位线性质简证“O是线段AD中点”的结论（如图4），具有“一眼望穿”求解之效．

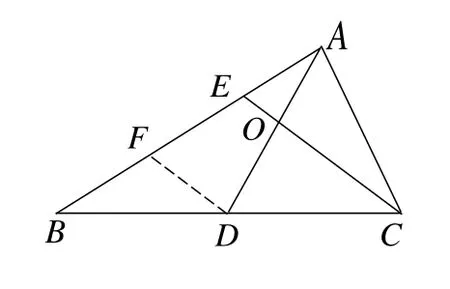
图4

【教学对策】高考数学选择题、填空题，主要以能力立意命题，从相当难度的角度区分学生思维能力的不同层次.一些考生解题方法或策略运用不当，反映选择题、填空题难算、耗时.其实，这都是考生思维层次不高、解题能力不强的表现.因此在做选择题、填空题时要注重解题方法和解题策略，处理好解题关系（小题大做，即使做对了也是隐性失分），优化解题认知结构，要把数、形结合起来作直观判断，要以数学知识及方法的系统化结构为基础作整体思维，要对数、式、形的结构和关系进行深刻洞察，纵横联系，大胆尝试、假设、特殊化，体现为解题过程简捷、迅速.

三、“隐而不发”——“难”解的隐性失分

所谓“隐而不发”，是指考生解答考题时，常因思维定式或思维缺乏严谨性，忽视数学试题存在隐含条件（隐含条件是一种在题目中未明确表达出来而又客观存在的条件，是命题者隐藏设计在试题中、不太容易发现的条件，在数学试题中具有一定的迷惑性），虽然解题过程可能完美无缺，但往往会产生“条件不足”的感觉而导致束手无策，解题难以解答下去，导致“隐而不发”——“难”解的隐性失分后果.

例3（2019年江苏高考第14题）设f(x)，g(x)是定义在R上的两个周期函数，f(x)的周期为 4，g(x)的周期为2，且f(x)是奇函数 .当x∈(0，2]时其中k＞0.若在区间（0，9]上，关于x的方程f(x)=g(x)有8个不同的实数根，则k的取值范围是_______.

【解析】本题考点为参数的取值范围，侧重函数方程的多个实根，如果不借助“数形结合”思想解题，难度较大.不少考生不能利用函数图象交点与周期性平移图象的“两个”隐念条件，找出两个函数图象相切或相交的临界交点个数情况（无法确定参数的取值范围），结果导致“隐而不发”——“难”解的隐性失分误区.同时，如果忽视函数定义域空心问题的隐念条件，解题就会出现“一失足成千古恨”错解的懊恼.

解题思维简析如下：

又f(x)为奇函数，其图象关于原点对称，其周期为4，如图5为函数f(x)与g(x)的图象，要使f(x)=g(x)在（0，9]上有8个实根，只需二者图象有8个交点即可.

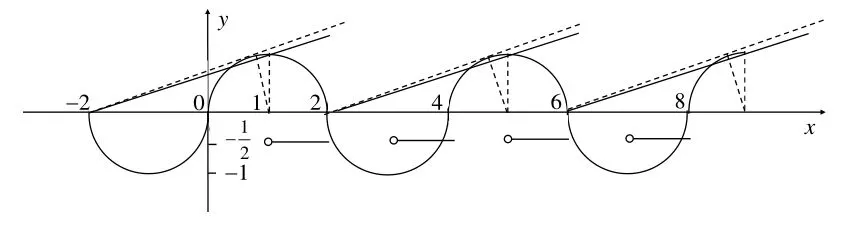
图5

【教学对策】隐含条件的挖掘能有效检验学生分析问题、解决问题的能力，高考试题中隐含条件可能隐藏在几何图形中（如试题中的字母、变量或关系式所隐含的几何图形的特征和位置关系），也可能隐藏在数学概念定义中（如试题所涉及的基本概念所属对象的性质，适合的数学模型或公式、定理、法则等），还可能隐藏在已知条件的相互联系中（如试题题设中的字母、变量或关系式所隐含的制约条件和取值范围）.因此，在平时数学解题教学中，要引导学生善于从数学概念之中，从公式的使用条件中，从变量的取值范围中，从题目的结构特征中，从题设条件的相互制约中，从题设的不变因素中，从式子的特殊结构中，从数形结合中挖掘隐含条件[3]，找到解题突破关键，发现解题契机，找到解题所缺的元素，从而使问题迎刃而解.

四、“对而不全”——“漏”解的隐性失分

所谓“对而不全”，是指考生解答考题时，面对有些数学试题题设或结论多种可能的情形，常因缺乏分类意识或思维的片面性，没有充分运用“化整为零”“积零为整”的思想与归类整理的方法，解答时只解出其中一种情形，而忽视了其他可能的情况，导致“对而不全”，造成“漏”解的隐性失分后果.

例4（2019年江苏高考第18题）如图6，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P，Q，并修建两段直线型道路PB，QA．规划要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A，B到直线l的距离分别为AC和BD（C，D为垂足），测得AB=10，AC=6，BD=12（单位：百米）．

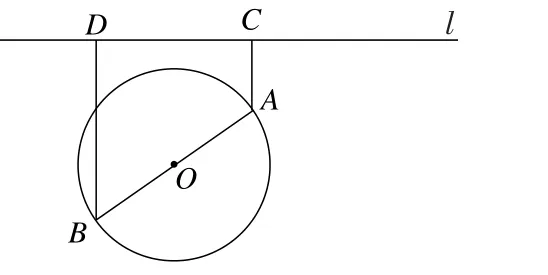
图6

（1）若道路PB与桥AB垂直，求道路PB的长；

（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；

（3）在规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P，Q两点间的距离．

【解析】本题主要考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.第（2）（3）题均需要分类讨论求解.不少考生缺乏分类意识，解答时分类不完全，导致“对而不全”，造成“漏”解的隐性失分后果.

解题思维简析如下（限于篇幅，解题过程略）：

（1）建立如图7所示空间直角坐标系，分别确定点P和点B的坐标，然后利用两点之间距离公式可得道路PB的长；PB=15.

图7

（2）分类讨论P和Q中能否有一个点选在D处即可.

参考答案：P和Q均不能选在D处.

（3）先讨论点P的位置，然后再讨论点Q的位置即可确定当d最小时，P，Q两点间的距离

【教学对策】分类讨论是一种重要的数学逻辑方法，也是高考数学的一种解题思想.分类讨论是历年数学高考命题的重点与热点，而且也是高考的一个难点.平时教学要加强分类讨论的解题思想训练，培养学生思维的严谨性和周密性，以及认识问题的全面性和深刻性.一是坚持分类讨论的“三原则”：分类的“全面性”（全域要确定，分类要“既不重复，也不遗漏”）、分类的“标准性”（在同一次分类中只能按所确定的一个标准进行）、分类的“逐级性”（对多级讨论，应逐级进行，不能越级）.二是熟习分类讨论的常见情形.由概念引起的分类讨论；由运算要求引起的分类讨论；由性质、定理、公式引起的分类讨论；由图形类型、位置引起的分类讨论；由参数变化引起的分类讨论[4].三是明确分类讨论的步骤.掌握分类标准，进行合理分类，做到不重不漏；逐类讨论，获得阶段性结果；归纳总结，得出结论.四是分类讨论的关注点.直接回避（如运用反证法、求补法、消参法等有时可以避开烦琐讨论）；按主元分类的结果应求并集；按参数分类的结果分类讨论 .