破解“重复运算”问题的若干策略

□吴志鹏

（福建省德化第一中学，福建德化 362500）

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等.通过高中数学课程的学习，学生能进一步发展数学运算能力，有效借助运算方法解决实际问题，通过运算促进数学思维发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神．数学问题的设计过程中，也经常会出现“在同一道题中，有多个同类型的运算对象，运算方法也相同的‘重复运算'”问题，那么在解题的过程中，就要经过两次或者更多次用同一种方法进行解答问题，浪费了时间，解题效率也会大大降低.那么怎样才能有效解决这类问题呢？笔者针对“重复运算”问题进行研究，发现可以利用以下几种策略减少运算次数，节约运算时间．

一、先求后补 提高运算效率

例1（2011年天津高考文科数学第8题）对实数a和b，定义运算“设函数f(x)=(x2-2)Ⓧ（x-1），x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点，则实数c的取值范围是（ ）

解：由题意得：

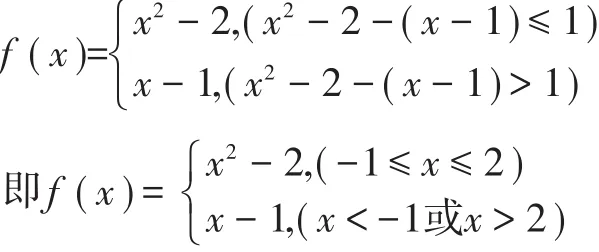
则f(x)的图象如图1所示：

图1

∵函数y=f(x)-c的图象与x轴恰有两个公共点，

即函数y=f(x)与y=c的图象有两个交点，由图象可得-2＜c≤ -1，或1＜c≤ 2.

变式（2019年全国卷Ⅲ理科数学第20题节选）已知函数f(x)=2x3-ax2+b.讨论f(x)的单调性.

解析：f′(x)=6x2-2ax=2x(3x-a)．

令f′(x)=0，得x=0或

若a＞0，则当时，；当时．故f(x)在单调递增，在单调递减；

若a=0，f(x)在(-∞，+∞)单调递增；

若a＜0，则当时，；当时．故f(x)在单调递增，在单调递减．

评析例1在分段函数“段”的处理过程中通过计算获得x2-2-(x-1)≤1得-1≤x≤2，此时若再求解x2-2-(x-1)＞1得结论：x＜-1或x＞2，必然浪费了时间.此时只需根据分段函数的定义域为R，分段函数在分段时各段的范围既不重复也不遗漏，可知各段的范围互为补集关系，由此分段时我们只需求解不等式x2-2-(x-1)≤1得-1≤x≤2，再求其补集得另一段的范围x＜-1或x＞2.这类例题比较多见，常出现在分类讨论时，如2019年全国卷Ⅲ理科数学第20题，讨论函数的单调区间也是如此，通过某个分类标准所确定的参数范围通常具有在某个区间内具有互补的特征，这样我们就可以利用补集的思想求解参数的讨论范围，而不必多次求解，提高运算效率，也减少了运算所需的时间.

二、正难则反 降低思维难度

例2男运动员6名，女运动员4名，其中男女队长各1人.选派5人外出比赛，队长中至少有1人参加，有多少种选派方法？

解：方法一（直接法）

方法二（间接法）

变式（2019年江苏高考第6题）从3名男同学和2名女同学中任选2名同学参加志愿者服务，则选出的2名同学中至少有1名女同学的概率是__．（答案）A，B两点，直线l2与C交于D，E两点，则的最小值为（ ）

评析有些排列组合问题，由于利用直接法需要分多种情况（这些情况相类似）进行讨论、解决与运算，不仅思维量增加了，计算量也同步增加，计算的失误率变得更高，有时如能进行反向思考、求解，则所求问题的情况减少了，这样不仅减少解题过程的思维量，更减少了计算量，对于获得正确的解题结果是很有帮助的．

三、整体替换 减少运算次数

例3（2017年课标卷Ⅰ理科数学第10题）已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于

A.16 B.14 C.12 D.10

解 析 ：设A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4),直线l1的方程为：y=k1(x-1)，联立方程得k12x2-2k12x-

根据题意，直线l1与直线l2互相垂直且斜率存在，所以有

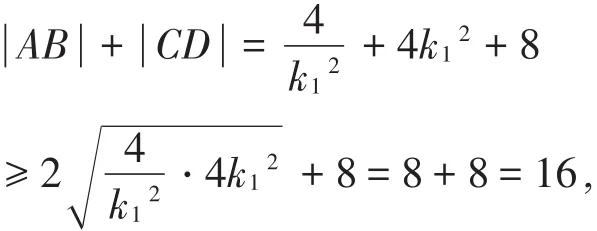
当且仅当k1=±1时取等号．

评析由于求弦长与|的方法同一，所以在解题过程中不要再一次进行求解，只需迁移求弦长| |AB的结论，将斜率用代入即可求得弦长| |CD，这样就能减少求解弦长运算次数，节约计算的时间.对于这类两条斜率相关或倾斜角相关的直线与圆锥曲线相交的问题，我们常常可先弄清其中一条直线与圆锥曲线的数量关系，再利用两直线的斜率关系进行代换，这样就能大大减少解题过程的运算量．

例4（2019年全国理科Ⅰ卷第19题）已知抛物线C：y2=3x的焦点为F，斜率为的直线l与C的交点为A，B，与x轴的交点为P．

所以l的方程为

所以y1+y2=2.从而-3y2+y2=2，故y2=-1，y1=3．

代入C的方程得

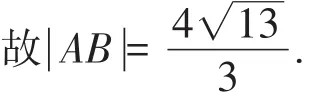
评析本题第（2）小题解法一为再次联立直线与抛物线方程进行消元获得根与系数的关系，用同一方法算两次，计算量增加了，此时若能根据直线x，y的联系，即，把y用含有x的整体进行代换，即可轻而易举地求得交点坐标，得到结论.显然第二种解法，解方程组运算的次数减少了，运算量也降低了．

四、先找后算 规范运算顺序

例5求直线l1:2x+y-4=0关于直线l:3x+4y-1=0的对称直线l2的方程？

解：直线l1:2x+y-4=0与直线l:3x+4y-1=0的交点为B(3，-2)，

在直线l1:2x+y-4=0取一点A(2，0)，设点A关于直线l:3x+4y-1=0的对称点为A′(x0，y0)，则有

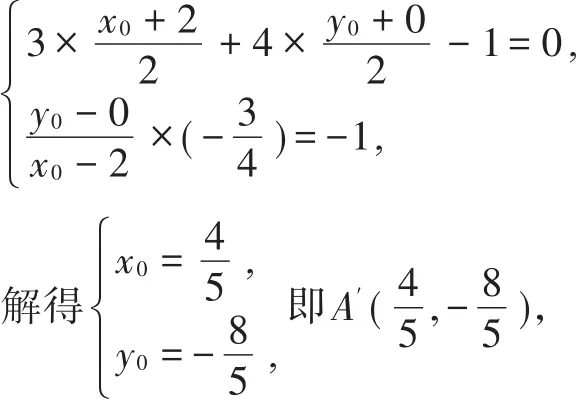
则直线l1:2x+y-4=0关于l:3x+4y-1=0 的 对 称 直 线 为即

评析本题求直线l1关于直线l的对称直线，只需在直线l1上任意找到两个点，并求其关于直线l的对称点，连接两个对称点求其直线方程即可，如果两次去求l1的点关于直线l的对称点，计算的方法是一样的，但计算量明显加大了，这时如能找到l1与l的交点，这一点同样也是对称直线与l的交点，这样求对称直线的方程也就简便了许多，计算量也减少了，因此规范运算顺序也能节约运算的时间．

例6（2019年北京高考理科数学第16题）如图2，在四棱锥P-ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且

（Ⅰ）求证：CD⊥平面PAD；

（Ⅱ）求二面角F-AE-P的余弦值；

（Ⅲ）设点G在PB上，且．判断直线AG是否在平面AEF内，说明理由．

图2

解析：（Ⅰ）由于PA⊥平面ABCD，CD⊂平面ABCD，则PA⊥CD，

由题意可知AD⊥CD，且PA∩AD=A，

由线面垂直的判定定理可得CD⊥平面PAD.

（Ⅱ）以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD，AP方向为y轴，z轴，建立如图3所示的空间直角坐标系A-xyz，

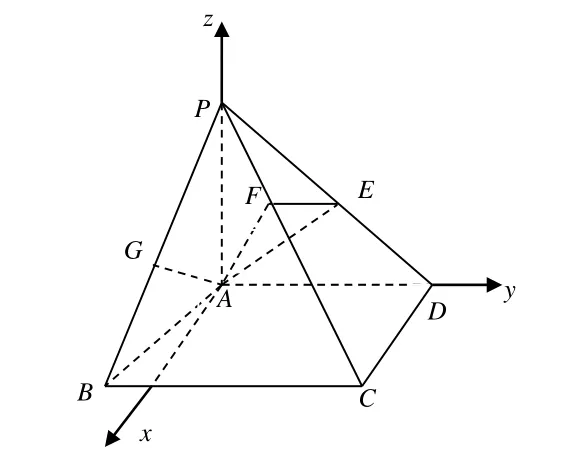
图3

由于平面AEP与平面YOZ重合，可得到平面AEP的一个法向量n=(1，0，0 )，

易知：

设平面AEF的法向量为：m=(x，y，z) ，则

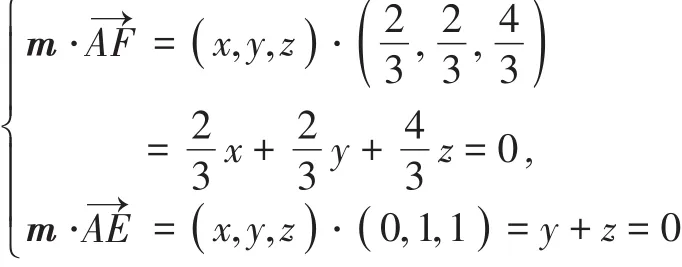
据此可得平面AEF的一个法向量为：m=(1，1，-1 )，

二面角F-AE-P的平面角为锐角，故二面角FAE-P的余弦值为

注意到平面AEF的一个法向量为：m=(1，1，-1) ，

m·且点A在平面AEF内，故直线AG在平面AEF内.

评析本题第（Ⅱ）小题要求两个平面的法向量，如果两次去求平面的法向量，虽然可行，但运算量却增加了，所以在解题时，我们应先观察，判断是否有与平面垂直的直线，如有则其方向向量为平面的一个法向量，这样我们就可以省去求一个平面法向量的时间，有效减少运算量，因此在运算过程中，如能规范运算的顺序则能节约运算时间，免除算两次的不必要．

五、简化结构 优化运算环境

例7已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点，求椭圆的方程．

解析：（1）若焦点在x轴上，设方程为

（2）若焦点在y轴上，设方程为

此时若能设椭圆方程为mx2+ny2=1(m＞ 0，n＞ 0，m≠n)．

变式（2019年浙江高考第2题）渐近线方程为x±y=0的双曲线的离心率是（ ）（答案C）

评析由于例7不清楚椭圆的焦点在x轴或y轴上，而要进行分类讨论，这样在运算的过程中就要计算两次才能获得结论，造成运算效率低下，如能利用圆锥曲线的统一形式对椭圆进行假设，就能简化方程的结构，优化运算的环境，减少运算次数，也有利于计算.变式问题如若设双曲线的方程为mx2-ny2=1(mn＞0)，再利用其渐近线方程为x±y=0，可避开对焦点在x轴和焦点在y轴两类双曲线情况的讨论，同样也能优化运算的环境，减少运算次数，便于计算．

总之，数学运算量的控制是与运算的思路、运算方法、运算途径的选择等密切相关的，教师只有在教学中不断帮助学生树立运算量控制的意识，降低运算难度，减少运算次数，使得学生自信于数学的运算，才能更好地提升学生的运算素养 .