数学“童画”，让思维的轨迹更清晰

李艳梅

[摘 要]数学“童画”是一种可视化的学习方式，它主张学生学会用数学的眼光把握、抽象事物的本质，用图式的方式表达思维过程。通过数学“童画”表示、说明、示意、猜测，让内涵“显出来”，让发现“说得清”，让思路“看得见”，让推理“说得通”，让特征“说得准”，从而让学生思维的轨迹更清晰。

[关键词]数学“童画”;思维轨迹;看得见

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2019）26-0033-03

数学“童画”是一种可视化的学习方式，是用感性的方式表达理性的思维。数学“童画”主张学生用数学的眼光把握、抽象事物的本质，用图式的方式表达思维的过程。现结合教学实际，谈谈如何通过数学“童画”，让学生思维的轨迹更清晰。

一、“童画”表示让内涵“显出来”

在核心素养下，数学教学要注重数学思想的渗透，特别是在小学阶段，数形结合思想的渗透更为重要。形是一种直观形式，学生能看得见，并能借助图形把一些概念和定律的内涵挖掘出来，有助于对一些概念和定律的理解。在理解中记忆和在理解中应用是进一步对知识的内化和深化，特别在“复习与整理”这一环节，让学生把对知识的理解用显性的图画表示出来，是对所学知识进行整合的过程，更是进一步建构知识的过程。

例如，教学苏教版教材四年级下册“运算定律”整理与练习第一课时时，我先让学生对所学的运算定律进行分类整理，然后提问：“你能用‘童画表示出每个运算定律吗？”学生纷纷表示“能够用‘童画表示”，并认真绘画。在学生的“童画”中，多数是画成交换两条长度不等的线段的位置，而用长度不变来表示加法交换律，用三条长度不同的线段表示加法结合律。从“童画”中可看出，对于三个数相加，可以先把前两个数相加再和第三数相加，还可以先把后两个数相加再和第一个数相加，它们的结果不变。学生在画图的过程中体会到加法结合律的内涵是运算顺序变了，而结果不变。用图表示乘法交换律时，多数学生画一个长方形，既可用长乘以宽求出这个长方形的面积，也可以用宽乘以长求出这个长方形的面积，因为面积是相等的，从而凸显了乘法交换律的本质：交换了两个乘数的位置，而结果不变。同样的一个长方形，可以用两种不同的方法求出它的周长，从而得出（a+b）×2=a×2+b×2，促进学生进一步理解乘法分配律的意义和模式。

二、“童画”说明，让发现“说得清”

学习数学一定要多问“为什么”，解释“为什么”就是对知识的来龙去脉的梳理，打通新旧知识的联系。依托数学“童画”的可视性，有助于学生分析问题，把握问题的关键，从而使问题迎刃而解。

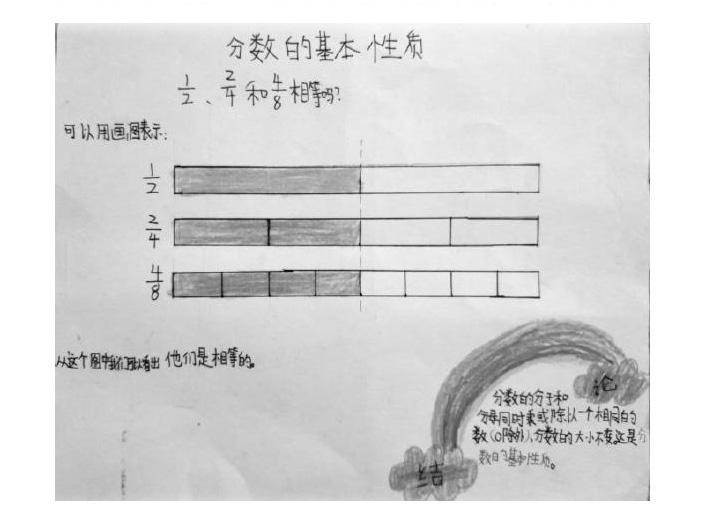
例如，在教学苏教版教材五年级下册“分数的基本性质”时，课始我讓学生在同样长的纸条上表示1/2、2/4和4/8，出示问题：1/2、2/4和4/8相等吗？学生在同样长的纸条上分别画出它的1/2、2/4和4/8，他们在画图的过程中对分数的意义有了进一步的理解和深化。从图中一眼就可看出1/2、2/4、4/8表示的长度是一样的，都是表示这个纸条长度的1/2，所以很容易得出结论：1/2=2/4=4/8。接着我追问：“它们的分子、分母都不相同，为什么它们的大小却相等呢？从中你又有什么发现？”学生对照图示分析分数中分子和分母的变化情况，很容易发现：从左往右看，分数的分子和分母同时扩大2倍，分数的大小不变;从右往左看，分数的分子和分母同时缩小2倍，分数的大小不变， 从而抽象概括出分数的基本性质。我继续追问：“我们都知道分数和除法有密切的关系，那么分数的基本性质和以前学过的什么性质是一样的呢？”学生对照图示想到了商不变的性质，从而理解了分数的基本性质为什么要强调“0除外”的道理。借助“童画” ，学生能发现规律并解释规律，找到新知和旧知的内在联系，从而打通知识间的联系，梳理知识，掌握规律，达到利用“童画”说明，让发现“说得清”的效果。

三、“童画”示意，让思路“看得见”

数学“童画”具有直观性，能够帮助学生理解抽象的语言所描述的复杂问题，利用“童画”进行直观示意，把抽象出的典型特征用特定的示意图表示出来，可以清晰地得出指向问题解决的“思维地图”，让思路“看得见”，利于学生用自己的语言把思维过程表达出来，从而解决了学生对抽象的语言描述、符号意义理解上的困难。

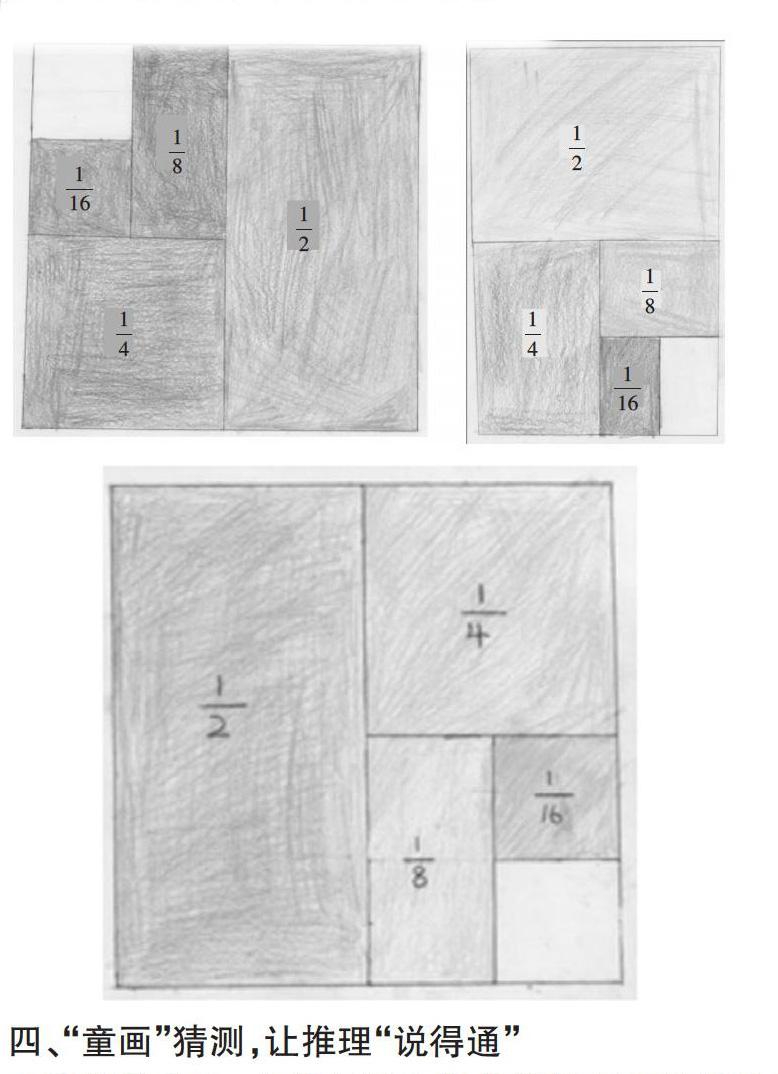
例如，在教学苏教版教材五年级下册“解决问题的策略——转化”第二课时时，我首先出示“[12+14+18+116+…+1256]”，然后提问：“你准备怎样解决这个问题？”多数学生都在沉思，没有一个学生说先通分再计算，说明他们意识到这种类型的题目不是用常规的方法就能解决的。于是我提示：“我们解决复杂问题时要从简单的问题着手，若要求[12+14+18+116]的值是多少该怎么做？现在请在一个图形上表示出每个加数，从图上你会有什么发现呢？”学生动手绘图（如下图），并根据图示发现：[12+14+18+116]的和是从单位“1”去掉[116]的部分，就是[1516]。 这时我引导学生观察这个加法算式中的加数 ，思考它们有什么特征，从而总结概括出解决这类问题的方法，即转化策略。这一过程是学生自主动手探索的过程，也是体会转化策略价值的过程。学生借助“童画”，把思考过程说得有条有理，很容易就能找到用转化策略解决实际问题的路径及价值所在，达到用数学“童画”表示，让思路“看得见”的效果。

四、“童画”猜测，让推理“说得通”

在数学教学中，应培养学生的合情推理和演绎推理能力，鼓励学生大胆猜测，并根据猜测进行推理和验证，激发学生参与探索知识的兴趣，鼓励学生再造数学知识生成的过程，从而让学生能有条理且清晰地表达自己的想法和看法。

例如，教学苏教版教材五年级下册“圆的面积公式”时，我设计了以下几个教学环节：

（1）猜测。你认为圆的面积与什么有关？圆的面积单位是平方厘米、平方分米、平方米，你认为圆的面积与什么有直接的关系？学生都认为圆的面积与半径有关，而根据圆的面积单位，部分学生推测出圆的面积与半径的平方有直接的关系。我接着追问：“圆的面积会与圆的半径的平方有什么样的关系呢？你能在圆上画一画、找一找吗？”

（2）尝试。学生在自己所画的圆上找它的面积与半径的平方的关系。有的学生在半圆上画出一个最大的三角形，三角形的底是圆的直径，高是圆的半径，于是得出三角形的面积是半径的平方，半圆的面积小于这样的三角形的2倍，大于一个三角形面积，从而推导出圆的面积是半径的平方的3倍多一些。还有的学生在圆心角90[°]的扇形上画一个边长和半径长度一样的正方形，则半径的平方表示一个边长和半径长度一样的正方形的面积，正方形的面积大于扇形的面积，从而推导出圆的面积比半径的平方的4倍要小一些。

（3）验证。“刚才仅仅是我们的猜测，还需进行验证，能不能把圆转化成我们学过的图形呢？”学生首先想到把圆转化成长方形，于是他们根据书上的提示动手画一画，小组内合作完成。在大家的共同努力下，学生用“童画”表示出从圆转化成长方形的过程。

（4）找联系。“我们把圆转化成长方形，在这过程中什么没变，什么变了？圆和长方形有什么内在联系？”学生对照图示，在小组内合作完成，找出它们之间内在的联系。不难发现，在转化的过程中，面积没变，长方形的长是圆周长的一半，长方形的宽是圆的半径，从而推导出圆的面积是它半径的平方的π 倍，从而验证刚才的猜测是正确的。

（5）总结概括。让学生再一次对照图示回顾刚才推测、验证的过程，在回顾的过程中，学生再一次体会把圆转化成长方形，面积没变，周长变，长方形的面积等于长×宽，长是πr，宽是r，从而得出圆的面积公式是S=πr2。

在上述教学中，教师引导学生直观画图，独立思考，并要求学生把自己的新想法和新体会在组内进行讨论交流，逐步构建起知识结构，形成知识模型，在积累数学活动经验的过程中领悟数学思想，从而达到“童画”猜测，让推理“说得通”的效果。

五、“童画”表达，让特征“说得准”

数学学习不光要让学生知道是什么，还要让学生经历探索认知的过程，并且用自己喜欢的方式表达获得知识的过程。学会用数学的方式去探索和思考是学习数学的关键，而将抽象的知识进行可视化的表达，可以降低学生学习的难度。数学“童画”能将抽象的知识用可视化的形式表达出来，具有直观性和生动性，非常有利于学生的思考和表达。因此，为学生营造一定的探索氛围和提供一定的现实背景是十分重要的。

例如，在教学苏教版教材五年级下册“3的倍数特征”时，我只让学生猜测3的倍数特征，多数学生都说个位上的数是3的倍数，那么这个数就是3的倍数;接着我让学生画图验证自己的猜测，学生画计数器表示数，很多学生列举了个位是3、6、9的数来验证自己的猜测，他们先举了13、16、19这三个数，很显然这三个数都不是3的倍数，然后他们在计数器上画出了是3的倍数的数字。从中可以发现，3的倍数特征与这个数的个位数字没有关系，而与这个数各个数位上数的和有关;各个数位上数字的和是3的倍数，那么这个数就是3的倍数。学生借助“童画”，很顺利地发现了3的倍数特征，并用自己的语言准确地总结概括出来。

总之，数学“童画”體现“以生为本”的理念，用儿童的表达方式构建和整合知识结构，促进新知从感性到理性的有效转化，让儿童的思维轨迹更清晰。

【本文系徐州市教育科学“十三五”规划课题“数学‘童画，让儿童的思维过程看得见”的实践研究（立项号：GH-13-18-L227）阶段性成果。】

（责编 黄春香）