齿轮箱断齿特征识别的S变换-SVD降噪组合方法

2019-10-10潘高元李舜酩杜华蓉朱彦祺

振动与冲击 2019年18期

潘高元，李舜酩，杜华蓉，朱彦祺

(南京航空航天大学能源与动力学院，南京 210016)

汽车的齿轮箱是传动系统中的重要组成部分，而齿轮箱中有60%的失效形式与齿轮有关[1]。齿轮常见的故障有齿面磨损、齿根裂纹、断齿等，其中断齿是最严重的损伤形式，直接影响机构的正常运转。齿轮元件在工作中发生局部故障，相应的特征将会表现在振动信号中。因此，通过对齿轮箱振动信号的采集和分析，找出故障源及其可能产生的原因，对确保齿轮箱及时、准确的维修和调试，具有重要的意义。在理想情况下，齿轮箱断齿故障信号中的冲击特征出现频率即为断齿旋转的频率。但是齿轮的故障信号往往是周期啮合振动、调幅、调频及附加脉冲的综合表现[2]，是典型的非平稳信号。这导致了故障源振动信号的冲击特征通常淹没在背景信号与噪声中，比较难以直接识别。因此，如何从带有噪声背景的信号中准确提取故障特征，进而进行齿轮箱的故障诊断是目前研究的热点问题。

S变换是最近发展起来的一种时频分析方法，在地球物理学领域已经证明了S变换的有效性，如分析内在的大气波包、大气研究、地震信号的鉴定、全球海洋表面温度分析、电气工程、机械工程、数字信号处理等。它和连续小波变换相同的是渐进分辨率，但和小波变换不同的是，S变换保留了绝对参考相位信息，且S变换不但可以估计局部的功率谱，还可以估计局部的相位谱，这也适用一般的复值时间序列。并且S变换克服了短时Fourier变换窗函数以及连续小波变换基函数固定不变的缺点，是一种高效的自适应信号时频分析方法，适合处理与分析非平稳信号，尤其是包含冲击特征的信号，其逆变换完全无损[3]。

奇异值分解(Singular Value Decomposition,SVD)降噪方法是一种非线性滤波方法，可以有效抑制信号中的宽带随机噪声。利用选取奇异值阈值的方式，可以减少信号中的噪声，提高信号识别的准确性[4]。而利用SVD对一维时域信号进行处理与分析，关键问题之一是构造合适的数据矩阵[5-6]。显然，需要得到能够明显识别冲击信号的矩阵，而S变换作为对冲击信号敏感的时频变换方法，在提取齿轮箱断齿特征方面非常合适于SVD的构造矩阵。

因此，基于S变换时频谱SVD降噪的冲击特征提取方法，能够很好的提取出信号中的冲击特征。而奇异值阈值的选择，则是此方法的关键之一。朱怡等[7-8]利用奇异值差分谱，选取奇异值差分谱最前面峰值群最后一个峰值的方式确定阈值位置，有效地提取轴承故障振动信号中的冲击特征频率。但是利用差分谱选取阈值的方法在一定条件下具有试探性，有时不能直观的挑选出阈值位置。此外，利用时域特征的进行冲击特征的识别，对轴承的某些故障特征频率识别已经足够，而行星齿轮箱行星轮断齿冲击特征比轴承的冲击特征更复杂，单独分析时域信息会导致特征识别不全。因此本文提出使用奇异值比值谱的方法，结合奇异值差分谱与奇异值比值谱选取阈值，能够在识别出冲击特征的情况下，直观的选择出奇异值阈值。并且在识别齿轮断齿冲击特征时，同时考虑时域特征和S变换的时频谱图，从而能够正确地识别出齿轮箱断齿故障。

1 S变换时频谱SVD降噪理论

1.1 齿轮断齿时域频域特征

齿轮断齿时的时域表现为幅值很大的冲击型振动，冲击频率理论上等于存在断齿轴的转频。在频域上表现为在啮合频率及其高次谐波附近出现间隔为断齿轴转频的边频带；边频带一般数量多、幅值较大、分布较宽[9]。

齿轮断齿的主要特征为：①以齿轮啮合频率及其高次谐波为载波频率，齿轮所在轴转频及其倍频为调制频率的啮合频率调制，调制边频带宽而高；②以齿轮各阶固有频率为载波频率，齿轮所在轴转频及其倍频为调制频率的齿轮共振频率调制，调制边频带宽而高；③振动能量(包括有效值、峰值等)有较大幅度的增加；④时域图中冲击频率等于有断齿轴的转频。

1.2 S变换

S变换是地球物理学家Stockwell提出的一种将信号从一维时域信号变换到二维时频的一种信号处理方法，其具有可逆性。其基本思想是对短时F变换和以Morlet小波为基本小波的连续小波变换的组合和延伸。可以将S变换认为是一种加了高斯窗函数且窗宽度与信号频率成反比的特殊的短时傅里叶变换STFT(Short-Time Fourier Transform)，因此在低频段具有较高的频率分辨率，在高频段具有较高的时间分辨率，并且对非平稳信号例如冲击信号十分敏感，满足线性叠加原理，不存在交叉项的干扰，是一种无损的且可逆的时频变换。

信号x(t)的S变换为

(1)

式中：f为频率；t为时间；b为时间轴上的位移参数。

1.3 SVD降噪理论

设矩阵A为m×n的矩阵，矩阵的秩为r，则必存在m×n的正交矩阵U和正交矩阵V，使得

A=USVT

(2)

(3)

即除了前r阶对角线元素外，矩阵S其他元素都为0，并且称σi(i=1,2,…，r)为矩阵A的奇异值。奇异值跟特征值类似，在矩阵中也是从大到小排列，奇异值大小其主要反映各元素的能量集中情况。而且奇异值减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。一般使用Hankel矩阵作为SVD的构造矩阵。由于冲击特征的幅值通常都呈指数衰减形式，此情况下Hankel矩阵不适合作为构造矩阵。而冲击信号在S变换的时频谱中比较集中，噪声信号则比较分散，因此S变换更适合作为SVD的构造矩阵。这样，奇异值中较大奇异值就主要反映信号的冲击成分，而较小的奇异值则反映信号的噪声与小的冲击部分。因此选择一定的奇异值设置阈值，将值较小的奇异值置零就可以消除部分噪声，使得冲击成分凸显出来。

2 奇异值阈值降噪方法与步骤

2.1 奇异值比值谱阈值降噪方法

奇异值阈值的选取决定了SVD降噪的效果，阈值数值过大会丢失重要的冲击信号，阈值数值过小则会使得降噪效果不明显。因此选择合适的阈值，在噪声降低的情况下不丢失冲击特征，是准确提取出冲击特征的关键之一。一种方法是利用奇异值差分谱的奇异值阈值确定方法来寻找合适的奇异值阈值[10]。定义奇异值差分谱为

P=(σ1-σ2,σ2-σ3,σ3-σ4,…,σr-1-σi)

(4)

由于奇异值按照降序排列，因此差分谱全部为正数。若仅选择奇异值差分谱最大峰值点对应的奇异值进行信号重构，会丢失一些弱冲击信号特征。为更好地保留信号的冲击特征成分，最大限度地抑制噪声成分，将奇异值差分谱中峰值群中最后一个峰值点序号对应的奇异值作为奇异值阈值[11]，能够很好地确定阈值的位置。所谓的峰值群，即为奇异值差分谱最前面部分较为集中的一组峰值点，并且其幅值显著大于后续峰值点的幅值。

但是这种方法确定阈值时在某些情况下具有试探性[12]，且有一定的人为选择的差异性，即在某些情况下峰值群的幅值无法显著大于后续峰值点的峰值，不能够直观的选取合适的位置。

结合Kanjilal等[13-14]仅使用前两个奇异值σ1/σ2的奇异值比谱(Singular Value Ratio,SVR)的方法，为了考虑全部奇异值，本文提出奇异值比值谱的方法对奇异值阈值进行选择。定义奇异值比值谱为

Q=(σ1/σ2,σ2/σ3,σ3/σ4,…,σi-1/σ1)

(5)

由于奇异值按照降序排列，因此比值谱全部大于一。同样的，选取奇异值比值谱中最前面峰值群的最后一个峰值点序号作为奇异值阈值。由于奇异值代表的是信号的能量集中情况，相邻的奇异值之间比值能够反映出变化趋势，在识别冲击特征上，和差分谱方法相比有异曲同工之妙。但是由于冲击特征的幅值通常都呈指数衰减形式，而且奇异值的前几个数都特别大，而后面的数值比较小，而S变换时频谱冲击特征更为集中，因此对于衰减较快的冲击特征，奇异值比值变化相比较差值变化更为明显，更容易选取出奇异值阈值。

此外，由于使用SVD降噪的方法对信号进行重构，使用信号的时域信息进行冲击信号分析，对冲击周期的倒数作为冲击信号的频率特征，因此实验数据的时间分辨率需要有足够的精度才能够准确获取冲击特征。如果信号的时间分辨率较差，当冲击信号时间间隔比较小时，一个时间分辨率误差就能引起较大的频率误差。因此若分析完信号发现特征的频率比较高，则需要考虑是否对信号重采样，重新计算以获取更准确的频率。若频率比较低，则对故障特征识别已经有足够的精度。

2.2 信号冲击特征提取的步骤

按照上述思路，为了从包含噪声的冲击信号x(t)中提取出冲击特征，对其进行S变换时频谱SVD降噪处理，其主要步骤如下：

步骤1对信号x(t)进行S变换，得到S变换时频谱系数矩阵A。

步骤2对S变换得到的时频谱矩阵A进行奇异值分解，得到矩阵A的奇异值，并将奇异值按照递减的顺序排列，即σ1≥σ2≥…≥σr。

步骤3求解其奇异值差分谱和比值谱并比较，选取奇异值比值谱中最前面峰值群的最后一个峰值点序号作为奇异值阈值，并设置为阈值σh，将奇异值序列中σh后的奇异值置为零，即对信号x(t)的S变换时频谱进行SVD降噪处理，然后重建S变换时频谱系数矩阵。

步骤4对重建后的时频谱矩阵进行S逆变换，得到x(t)降噪后的时域冲击特征，根据冲击特征的时间差值得到冲击的周期，从而得到冲击信号的特征频率。

步骤5结合判断S变换后的二维时频矩阵，判断x(t)时域特征的信息是否正确完整，并根据采样的时间分辨率以及得到冲击特征频率值大小判断是否需要重新采样。

3 仿真信号分析

3.1 较高信噪比信号仿真分析

仿真设计的冲击信号x(t)的冲击成分由以下的指数衰减形成

P(t)=e-ξωnπt×cos(2πft)

(6)

图1 冲击信号p(t)Fig.1 Impact signal p(t)

首先，对信号x(t)进行S变换，得到其时频矩阵，其云图如图2所示。从图2中可以看出，在相对频率为8 Hz左右出现十分明显的冲击信号，说明S变换识别冲击特征的效果还是十分明显的。

图2 信号x(t)的S变换时频谱图Fig.2 S-transform time-frequency spectrum of the signal x(t)

其次，对信号x(t)的S变换时频矩阵进行SVD奇异值分解，求得其奇异值，并将奇异值按照降序排列。由于奇异值主要信息存储在前面较大的奇异值之中，因此只显示其前一百个奇异值，如图3所示。从图3可以看出在第75个奇异值之后趋势变化已经非常缓慢，基本接近于零。

然后，对奇异值进行差分谱和比值谱的求解，分别按照式(4)、式(5)所定义的公式进行计算，得到的奇异值差分谱和比值谱的曲线如图4和图5所示。

图3 S变换时频谱矩阵的奇异值谱Fig.3 Singular value spectrum of S-transform spectrum time-frequency matrix

图4 S变换时频矩阵的奇异值谱的差分谱Fig.4 Singular value difference spectrum of S-transform spectrum time-frequency matrix

图5 S变换时频矩阵的奇异值谱的比值谱Fig.5 Singular value ratio spectrum of S-transform spectrum time-frequency matrix

最后，对信号进行降噪，重构时域信号。由于信号信噪比高，因此奇异值应该保留的多而置零的少。可以看出，奇异值最前面的峰值群上的最后一个峰值点，根据差分谱的结果，由于峰值一直衰减，在选取阈值时选第26个还是第31个还是第46个，存在人为选择的差异，具有不确定性，很难直接按照峰值群进行判断。而奇异值比值谱则明显能看出，在第46个奇异值位置，比值谱的峰值就已经都能够明显的与后面的峰值分辨开。

因此，根据奇异值差分谱的结果，本次选则将第31个奇异值之后的奇异值置零，重建S变换时频矩阵，然后进行S逆变换得到降噪后的信号时域图如图6(a)所示。根据比值谱的结果，将第46个奇异值之后的奇异值置零，重建S变换时频矩阵，然后进行S逆变换得到降噪后的信号时域图如图6(b)所示。可以看出根据奇异值比值谱的方法选取阈值。尽管保留的奇异值比差分谱方法多，但是已经能够提取出信号的冲击特征，噪声在时域特征上已经很少，相比较差分谱选择阈值的方式，比值谱方法在提取冲击特征的同时保留了更多的冲击特征，并且比值谱方法更容易判断出阈值的位置。

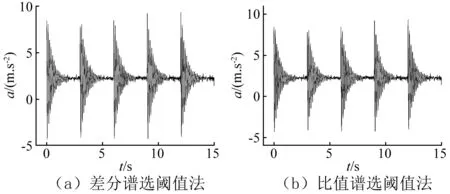
图6 x(t)选取不同阈值降噪后的冲击信号Fig.6 The denoised impact signal using different thresholds

3.2 低信噪比信号仿真分析

仿真冲击信号x(t)的冲击成分p(t)与不含噪声的冲击信号相同，在信号中添加的幅值序列均值为1，标准差为0.3的高斯随机序列噪声。含噪声的冲击信号x(t)的时域图如图7所示。

图7 含高斯噪声的x(t)冲击信号Fig.7 Impact signal x(t) with Gaussian noise

同样按照前面所述的信号分析步骤，首先对信号x(t)其进行S变换，得到的S变换时频图如图8所示，可以看出在8 Hz左右仍然能看到冲击特征，但是冲击特征很不明显，说明冲击信号淹没在噪声中。其次对S变换的时频矩阵进行SVD奇异值分解，并将奇异值按照降序排列，选取其中前100个奇异值如图9所示。然后同样的计算出奇异值差分谱和比值谱曲线，如图10和图11所示。

图8 信号x(t)的S变换时频谱图Fig.8 S-transform time-frequency spectrum of the signal x(t)

图9 S变换时频谱矩阵的奇异值谱Fig.9 Singular value spectrum of S-transform spectrum time-frequency matrix

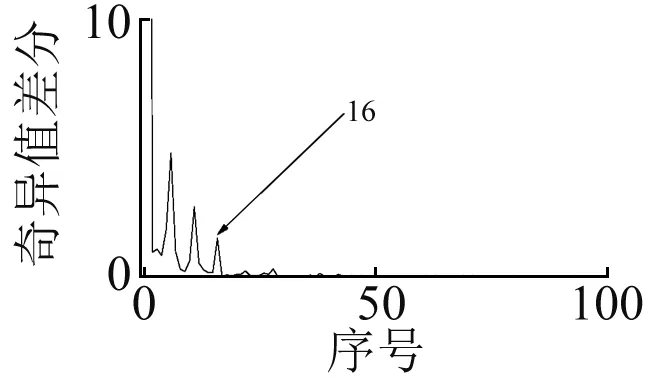
图10 S变换时频矩阵的奇异值谱的差分谱Fig.10 Singular value difference spectrum of S-transform spectrum time-frequency matrix

图11 S变换时频矩阵的奇异值谱的比值谱Fig.11 Singular value ratio spectrum of S-transform spectrum time-frequency matrix

从图10和图11可以看出，差分谱和比值谱中最前面部分出现峰值群，都以峰值群中最后一个峰值点的序号16作为奇异值阈值的位置坐标，即选择阈值σh=16，对后面的奇异值进行置零。但是比值谱曲线的最后一个峰值变化显然比差分谱曲线更明显。然后重建S变换降噪后的时频矩阵，对其进行S逆变换，从而得到SVD降噪处理后的时域信号，如图12所示。

图12 x(t)降噪后冲击信号Fig.12 The denoised impact signal of x(t)

由图12结果可以看出，利用奇异值差分谱和比值谱，都可以保留源信号的主要冲击成分，将其从噪声中提取出来，而且两者选择阈值是一致的。而奇异值比值谱的方式，第16个位置处的幅值比后面差别更大，选取阈值时候更直观。

综上，当信噪比较低时，比值谱和差分谱都能够筛选出接近一致的阈值，提取出信号中的冲击信号；而当信噪比较高时，比值谱能够保留更多的冲击信息。相比较之下，使用奇异值比值谱选取阈值的方式，其峰值群的变化更大，更容易直接选取合适的阈值。

4 齿轮箱断齿振动信号分析

4.1 实验设备与基本参数

为验证奇异值比值谱选取阈值的方法在齿轮箱断齿故障信号中提取冲击特征的有效性与实用性，下面采用实验进行方法的验证。

实验采用电机-齿轮箱-负载转盘的形式进行连接，断开转盘与发动机的连接，部件之间用联轴器连接，设备的连接图如图13所示。电机型号为WF2-180L-4，运行工况电机恒定转速。齿轮箱采用降速的形式进行连接，即输入轴太阳轮转速等于电机转速n=1 500 r/min。传感器采用振动加速度传感器，连接如图14所示。齿轮箱为一级行星齿轮箱，为3个行星轮，1个太阳轮，1个固定内齿圈，行星架为输出，主要参数参见表1。齿轮故障类型为其中一个行星轮断一个齿，如图15所示。

图13 齿轮箱设备连接图Fig.13 Gearbox equipment connection

图14 齿轮箱加速度传感器位置Fig.14 Position of gearbox acceleration sensor

图15 齿轮箱行星轮故障齿轮Fig.15 Fault gear of gearbox planetary gear

表1 测试齿轮箱参数Tab.1 Parameters of the test gearbox

为了获得完整的冲击信号频率特征，需要获取至少两个周期的时间序列；为了提高计算效率，则时间序列长度不能过大。实验设置采样频率为fs=12.8 kHz，时间分辨率为t=7.812 5×10-5s，根据电机的转速可知，截取采样点数N=4 096就已经达到了分析的要求。

4.2 实验信号分析

选取输入端太阳轮处的加速度传感器的进行分析，加速度信号沿齿轮轴的径向方向。实验所测得的故障齿轮箱的振动加速度时域信号y(t),如图16所示。

图16 故障齿轮的原振动加速度信号y(t)Fig.16 The original vibration acceleration signal y(t) of the fault gear

对时域信号进行自相关处理，然后进行FFT(Fast Fourier Transformation)计算得到频谱图，可以得到主要信号的基频为fn=25 Hz。由实验参数可知太阳轮基频为1 500/60=25 Hz，与实验参数电机转速相符。根据齿轮的传动比以及齿轮齿数可知，其太阳轮基频为25 Hz，输出端行星架基频为8.33 Hz。

首先对所得信号进行FFT，得到信号的自功率谱图，如图17所示。从自功率谱图可以看出，齿轮的整个信号主要集中在基频25 Hz以及其倍频段和500～850 Hz的频段。因此取0～1 000 Hz的自功率谱图的局部放大图,如图18所示。

图17 信号y(t)的自功率图Fig.17 Autopower of the signal y(t)

图18 信号y(t)自功率图的局部放大图Fig.18 Partial enlargement of the autopower diagram of the signal y(t)

在500 Hz以下的频率，除了太阳轮自转的基频25 Hz外，主要由50 Hz，75 Hz，200 Hz，300 Hz，400 Hz等基频的倍频组成，加速度振动幅值较小。而在600.13 Hz等处能量比较集中，在583.50 Hz，591.75 Hz，608.38 Hz，616.75 Hz，625.13 Hz，633.50 Hz，641.75 Hz，650.13 Hz，691.75 Hz，716.75 Hz等频率，相邻的幅值的差值基本上在8.25～8.38 Hz，在误差范围内基本为输出轴的转动的基频。使用FFT主要获取以上频率信息。

按照S变换SVD降噪的方法，首先对时域数据进行S变换，得到的S变换的时频图如图19所示。可以看出，在信号的相对频率700 Hz左右出现比较明显的冲击特征，在相对频率1 500 Hz以上基本没有冲击信号。

图19 信号y(t)的S变换时频谱图Fig.19 S-transform time-frequency spectrum of the signal y(t)

然后对S变换后的时频矩阵进行SVD奇异值分解。根据奇异值的特点，选取其前一百个奇异值进行分析，其差分谱和比值谱，分别如图20和图21所示。

由奇异值差分谱与比值谱可以判断，两者总趋势是一致的，但是每个图在不同的局部(例如第10个峰值)却是不一样的。综合考虑两个曲线，选择第23个奇异值处作为奇异值置零的阈值，对此奇异值后面的奇异值进行归零处理，重建S变换时频矩阵，然后对其进行SVD逆运算，得到降噪后的S变换的时频矩阵。最后对时频矩阵进行S变换逆变换，得到降噪后的时域的冲击信号如图22所示。

图20 S变换时频矩阵的奇异值谱的差分谱Fig.20 Singular value difference spectrum of S-transform spectrum time-frequency matrix

图21 S变换时频矩阵的奇异值谱的比值谱Fig.21 Singular value ratio spectrum of S-transform spectrum time-frequency matrix

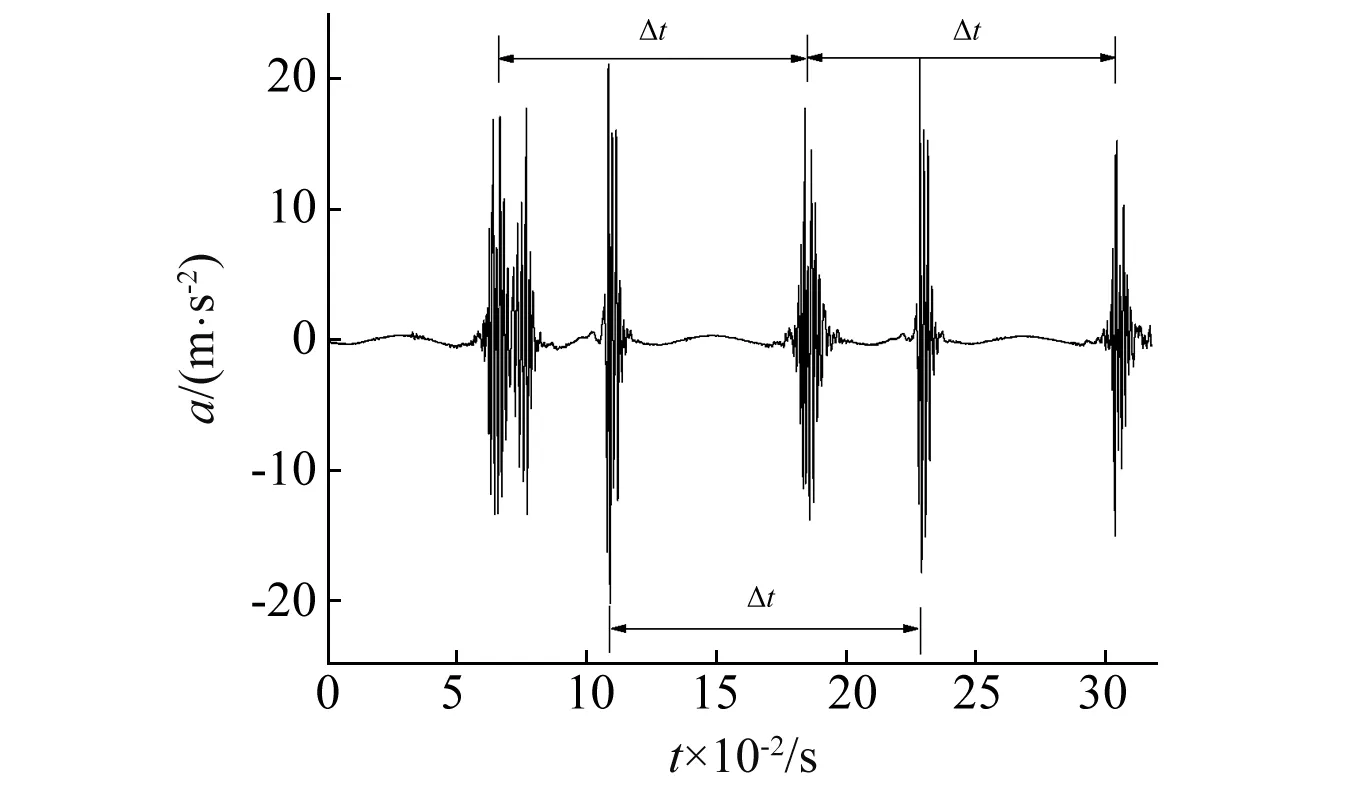
图22 y(t)降噪后时域信号Fig.22 The denoised impact signal of y(t)

从降噪后的时域图可以得到冲击信号的几个时刻点，分别在0.064 3 s，0.076 95 s，0.108 7 s，0.184 2 s，0.228 4 s，0.304 3 s处，相邻的两个时间差值的倒数从13.17～98.5 Hz不等，与齿轮断齿的信号频率完全不符。究其原因，与滚动轴承内圈、外圈故障不同，对于行星齿轮箱而言，行星齿轮和保持架内圈齿以及太阳轮齿轮同时啮合，因此单个的行星齿轮断齿会在不同的时间冲击太阳轮和保持架内齿圈，因此两个信号的周期是相互重叠的，对太阳轮的两个冲击信号时域间会带有对保持架内齿圈的冲击信号，对保持架同理。因此，单纯的判断降噪后的时域信息，对行星齿轮而言是不能得到正确的冲击信号。因此结合S变换的时频矩阵进行分析，舍去基本无冲击信号的频率部分，得到S变换的二维时频云图的局部放大图，如图23所示。