基于通用选择性分数重复控制的磁悬浮转子谐波电流抑制
2019-10-10崔培玲张国玺刘志远韩邦成
崔培玲, 张国玺, 刘志远, 许 涵, 韩邦成
(北京航空航天大学 仪器科学与光电工程学院,北京 100191)
磁悬浮控制力矩陀螺是超静卫星平台姿态控制的理想惯性执行机构[1-3],而磁悬浮转子(Magnetically Suspended Rotor, MSR)系统则是磁悬浮控制力矩陀螺的主要组成部分。在磁悬浮转子系统中,转子的质量不平衡[4]和传感器误差[5]会在磁轴承励磁线圈中产生谐波电流,从而造成谐波振动[6-7]。这种振动会通过陀螺基座传递到卫星平台,进而对平台上高精度的成像装置产生不利影响[8]。因此,对磁悬浮转子系统中谐波电流的抑制具有重要意义。
基于内模原理的重复控制(Repetitive Control, RC)[9],是一种能有效地消除周期性干扰信号,实现零稳态误差的控制方法。通过将干扰信号的内部模型嵌入到一个稳定的反馈系统中,在基波和高次谐波频率处产生无穷增益,从而达到抑制谐波的目的。目前RC已被应用于多个领域,如电力电子变换器[10],电机驱动器[11]以及各种类型的磁悬浮转子系统[12-14]。为抑制磁悬浮电机主轴由于自身不平衡力和电机不平衡磁力产生的振动,Zhang等提出了一种复合重复控制方法,既可以抑制掉主轴本身由于不平衡力产生的振动,又可以消除电机控制电流中的谐波成分,取得了很好的实验效果。
然而,RC在实际应用中存在一定的局限性。一方面,重复控制器长度N由系统采样频率和外界周期性干扰信号基频的比值确定,在数字域中实现时,其物理意义为寄存器延时单元的个数。因此离散RC控制器的长度必须保证为整数。然而在实际应用中,系统采样频率往往固定不变,周期性干扰信号的基频却可能处于任意频率段,这样采样频率和基频的比值就会出现分数。当该比值为分数时,现有的传统重复控制器(Conventional RC, CRC)往往会对分数就近取整近似作为控制器长度,但这样会导致控制器对干扰信号的抑制性能严重下降[15]。为了解决这个问题,文献[16]根据基波频率实时改变采样率以保证两者的比值为整数。然而这种方法大大增加了控制系统的复杂度和计算负担,特别是当谐波频率在较大频带范围内变化时,此问题更加突出。文献[17-18]则通过将控制器延时的分数部分用拉格朗日插值多项式组成的有限脉冲响应滤波器(Finite-Impulse-Response, FIR)近似代替,取得了良好的近似效果。这种方法对控制器计算能力要求不高,适用于大多数的控制系统。
另一方面,在系统带宽范围内,CRC均等地抑制所有谐波频率点处的谐波分量。然而在实际系统中,谐波通常只集中在一些特定的谐波频率点处而非整个频带。例如,在磁悬浮转子系统中,谐波分量通常并不均匀分布,低频谐波分量往往表现为主导谐波。因此仅抑制特定频率处的谐波分量,或者仅针对某些频率处的主导谐波分量,就能达到预期的控制目的。同时,由于控制系统采样频率一般很高,干扰信号基频相对较低,导致CRC控制器长度一般很长,其输出更新所需要的时间就会很长,导致其动态响应相对很慢,不能很好地满足控制系统快响应的要求。
谐振控制[19],以及基于离散傅里叶变换的RC[20]等控制方法可以对主导谐波进行选择性抑制,从而加速收敛过程。然而,这些控制器的设计比较复杂,计算负担也相对很大。文献[21-22]提出了一种并行结构的重复控制策略,以实现选择性谐波抑制,加速动态收敛过程,同时其计算量相较于CRC没有增加。但是以电力电子系统中为应用背景提出的这种控制策略,不能直接应用于磁悬浮转子系统。首先,转子系统的精确模型未知,并且由于系统的不确定性和强未知干扰,使系统绝对稳定的相位补偿器不能参考Lu等研究中的电力电子系统一般取作逆系统。其次,当重复控制器插入到原闭环系统时,由于转子系统固有的不稳定性,控制系统易失稳甚至陷入崩溃。因此,需要设计合适的系统补偿器保持整个系统的绝对稳定。同时,Lu等仅通过在频域内进行极点配置给出了并行结构重复控制的传递函数,继而通过极点位置说明这种结构在相应的频率处可以产生无穷增益,由此消除对应频率处的谐波分量,而并没有对时域周期信号进行理论分析,从而给出其信号内模。
基于上述分析,本文提出了一种通用选择性分数阶重复控制器(Universal Selective Fractional Repetitive Controller, USFRC),对磁悬浮转子系统的谐波电流进行选择性抑制。相较于传统重复控制器,这种控制器的动态响应明显加快,同时没有增加额外的设计和实现复杂性,并且可以根据实际控制需求灵活变换为现有各种形式的RC控制器。
本文首先建立了kn+i阶离散周期序列的信号发生器,它能补偿kn+i阶周期谐波信号;其次,给出了USFRC控制器一般形式及其在MSR系统中的稳定判据;然后,针对MSR系统和稳定性判据,给出了一种相位补偿策略;最后,对该方法的有效性进行了验证。
本文中所用的符号均是标准符号。为了简化,H(z)的频率响应函数H(ejωTs用H(ω)代替。
1 通用选择性分数阶重复控制器
1.1 kn+i阶序列的内模
对于一个周期为N∈的离散时间序列x(m)∈,如果它只包含kn+i次谐波分量,其中N=T0/Ts,T0为其基波周期,Ts为系统采样周期;k,n和i∈,0≤i 定理1周期序列x(m)是一个kn+i阶谐波序列的充要条件是等式e±j2πi/nx(m)=x(m±N/n)成立。证明: 1) 充分性。对于只包含kn+i次谐波分量的离散周期序列x(m),可表示为如下的傅里叶级数形式 (1) 式中:cl为傅里叶级数系数,进一步可表示为 (2) 由于x(m)只包含kn+i次谐波分量,则当l=kn+i时,cl≠0;l≠kn+i时,cl=0。则有 (3) 2) 必要性。假设离散周期序列x(m)满足 (4) 证毕。 假设有一周期序列x1(m)满足 (5) 令σi=ej2πi/n,根据定理1,有 (6) 则x(m)可以重写为 (7) 式(7)经z变换得 (8) 如果x1(m)只包含kn+i次谐波分量,根据定理1,可以得到x1(m)=σix1(m-N/n),经z变换可得 X1(z)=σiz-N/nX1(z) (9) 因此 (10) 式中:Gkn+i(z)为kn+i阶谐波序列内模的脉冲传递函数,其极点位于j(kn+i)ω0,ω0=2πT0为基波角频率。 注意到,当n和i取不同值时,Gkn+i(z)可以得到不同的内模。例如,当n=1,i=0时,Gkn+i(z)为传统RC内模;当n=2,i=1时,为奇次RC内模[23];当n=2,i=0时,为偶次RC内模[24];当n=6,i=1时,为6k+1 RC内模;以此类推。很明显,本文提出的kn+i阶RC内模Gkn+i(z)是各种现有RC内模的一种通用形式。 图1为kn+i阶谐波信号内模结构框图。 图1 kn+i阶谐波序列内模Gkn+i(z)结构图Fig.1 The diagram of the internal model Gkn+i(z) of the kn+i order harmonic sequence 值得注意的是,如图1所示,数字控制器Gkn+i(z)是由N/n个寄存器延时单元来实现的。当N/n是整数,也即一个信号周期内的采样点数N可由n整除时,控制器Gkn+i(z)可以完全抑制kn+i次谐波分量。然而在实际MSR系统中,采样频率往往固定不变,若使得N/n为整数,和谐波周期密切相关的转子转速就会被限制在某些特定区域。否则,N/n就会出现分数,进而导致其抑制精度降低。同时,在这种情况下,系统原有的稳定性有可能会被破坏。 在实际工程应用中,由于转速会在较大范围内变化,N/n通常都会出现分数情况。为保证控制器的抑制性能不发生严重下降,需要对分数部分做出适当处理。目前主要有两类方法:一类方法,如Kimura等所述,通过实时改变系统采样周期使得N/n为整数,但是该方法实现的复杂程度和计算成本都会显著增加,尤其当转速在大范围内变化时;另一类方法,通过利用拉格朗日插值多项式构成的FIR滤波器来近似分数部分,这种方法计算成本有限,近似程度较高,可很好的解决分数部分带来的系统性能下降的问题,适用于有限计算能力情况下的工程应用。 一般地,本文中N/n看作分数,采用由拉格朗日插值多项式构成的FIR滤波器实现分数部分的近似。 图1为一种理想状况下的kn+i阶重复控制器内模,由于Gkn+i(z)在单位圆上产生的无穷极点,导致控制器本身具有潜在的不稳定性。同时系统模型和参数的不确定性以及高频扰动分量等诸多因素可能导致系统失稳。因此,通常采用滤波器来提高整个系统在实际应用中的稳定性。此外,还引入内模控制增益调节系统鲁棒性和瞬态响应。 图2中从i(z)~ic(z)的USFRC控制器的传递函数可以表示为 CUSFRC(z)=[k0G0(z)+…+kiGi(z)+…+krGr(z)]C(z) (11) 分数阶部分z-A可由拉格朗日插值多项式构成的FIR滤波器H(z)近似。具体地 (12) 图2 通用选择性分数阶重复控制器结构框图Fig.2 The block diagram of the proposed USFRC 本文所研究的MSR系统的控制框图如图3所示,USFRC控制器通过插入方式连接到磁悬浮转子系统的反馈回路中。图中,Gc(z)为反馈控制器,保证了初始闭环MSR系统的稳定性,一般为PID控制器;Gw(z)和Gp(z)分别为功率放大器和转子系统的传递函数;ks为位移传感器的增益;r(z)为给定的转子位置参考信号;xd(z)为等效的转子质量不平衡和传感器谐波干扰信号;i(z)为功率放大器输出的控制电流信号,其中包含不必要的谐波成分;ic(z)为经过USFRC控制器处理后的电流信号。 如图3所示,系统函数可以定义为 (13) 定义C(z)的频率特性为C(ω)=Ac(ω)ejθc(ω),其中Ac(ω)为幅值,θc(ω)为相角。同样地,F(ω)=Af(ω)ejθf(ω),其中Af(ω)为幅值,θf(ω)为相角;Q(ω)=Aq(ω)ejθq(ω),其中Aq(ω)为幅值,θq(ω)为相角。根据上述定义,记M(ω)=Ac(ω)Af(ω)Aq(ω)和θ(ω)=θc(ω)+θf(ω)+LωTs,可以得到 图3 USFRC-MSR控制系统结构框图Fig.3 Plug-in USFRC-controlled MSR system (14) 基于上述变量定义,可以得到如下稳定性判据: (15) 以及 90°<θ(ω)<270° (16) 证明: 图3所示的闭环控制系统的传递函数为 (17) 其中, (18) FIR滤波器H(z)可以表示为 (19) 令z=|z|ejωTs,|z|=a,可以得到 (20) (21) 如果(bcosθi-1)≥0,有 (22) 如果(bcosθi-1)<0,∀|z|=a≥1,有 (23) 由此,∀|z|=a≥1,可以得到 (24) 因此 (25) 则系统闭环特征方程可以写为 (26) 假设式(26)中虚部为零,由cosθ(ω)<0,有 (27) 由式(27)可知,系统的传递函数G(z)所有极点pi(i=0,1,2,…,r)均位于单位圆内。由于ki以及M(ω)在实际控制系统中均为正值,因此如果条件式(15)成立,则条件式(16)一定成立。 本文利用Cui等研究中的磁悬浮转子控制系统模型作为算例验证USFRC控制算法的可行性和有效性。其中控制器Gc(z),Gp(z)以及Gw(z)可由下列Gc(s),Gp(s)以及Gw(s)的表达式经过Tustin变换离散化得到,离散时间为系统采样时间Ts 仿真参数如表1所示。 表1 磁悬浮转子系统参数 图4所示为系统函数F(z)的伯德图,系统初始相位θf(ω)∈(-90°,270°)。根据相位稳定条件式(16),需要合理设计相位补偿器以使得系统稳定。 图4 系统函数F(z)的伯德图Fig.4 Phase bode plot of F(z) 相位补偿环节可分为两部分:C(z)以及L(z)。C(z)补偿系统的中低频相位,L(z)补偿系统高频部分的相位滞后。本文中考虑转子转速为60 Hz,主导谐波电流一般出现在1次、2次、3次、5次以及7次谐波频率处。考虑到系统不确定性以及噪声的影响,系统截止频率ωc设计为6 230 rad/s (1 000 Hz),因此只需要考虑系统函数F(z)在(0, 1 000) Hz内的相位特性。 从图4可以看出,当频率为6 230 rad/s时,系统相位大约是-90°,为了满足相位稳定条件式(16),需要满足 180° (28) 即 2.5 (29) 由于L为整数,本文中L取值为4。同时,根据Cui等的研究可以得到下列补偿器C(z) (30) 图5给出了经过相位补偿后的系统函数与原始系统函数的相位伯德图。在频率范围ω∈(0,ωc)内,由图5可得补偿后的系统相位θ(ω)∈(138.8°,216.7°),因此有min|cosθ(ω)|=0.76。图6给出了相位补偿后的系统的幅频响应。从图中可以得到,max{F(ω)C(ω)}=max{M(ω)}=1.6 dB。 图5 相位-频率响应Fig.5 Phase-frequency diagram 进一步地,考虑到系统鲁棒性,定义系统模型的不确定度为Δ(z),且满足|Δ(z)|≤ρ,其中ρ为一个正的常数。假设Δ(z)是稳定的,则根据文献[25],稳定条件式(15)可以重写为 (31) 图6 相位补偿后系统的幅频响应Fig.6 Magnitude-frequency diagram of C(z)L(z)F(z) 仿真中,设置谐波电流基波频率f0为60 Hz。图7为磁悬浮转子仿真系统产生的谐波电流时域图,图8为其频域图。 图7 无RC控制器时磁悬浮转子系统的谐波电流(时域)Fig.7 The current under the initial closed-loop system without RC controller (time-domain) 图8 无RC控制器时磁悬浮转子系统的谐波电流(频域)Fig.8 The current under the initial closed-loop system without RC controller (frequency-domain) 从图8可以看出,在频率范围ω∈(0,ωc)内,相较于其他频率点处的谐波分量,1次、2次、3次、5次以及7次谐波分量有更大的幅值,约占控制电流谐波成分的99%。因此8k+i次谐波分量为主导谐波,其中n=8,且主导谐波最高阶次r=7。为抑制上述主导谐波,由图2可知,至少需要5个内模控制器并联。在仿真中,分别选取i为1,2,3,5和7构成USFRC控制器。 为了验证本文所提出的USFRC控制器的有效性,将USFRC与Xu等研究中的重复控制器进行了对比。由图7可知谐波信号1次谐波的幅值是最大的,其次是2次和3次谐波,幅值相对较小的是5次和7次谐波。一般地,控制增益越大,其对应内模控制器动态性能越好。因此,为了使系统稳定以及获得更好的收敛性能,由前所述,支路增益应满足k1+k2+k3+k5+k7≤0.86,k1>k2≥k3>k7≥k5。仿真中,实际选取增益和k1+k2+k3+k5+k7=0.8。 图9给出了谐波电流在时域内的瞬态响应。具体地,图9(a)为加入Xu等研究中所述传统重复控制器后电流的瞬态响应,当谐波电流收敛到6 mA附近时,其收敛时间为0.5 s;图9(b)和图9(c)为加入本文提出的USFRC控制算法后电流的瞬态响应,其中图9(b)中USFRC控制器的支路增益比为k1∶k2∶k3∶k5∶k7=1∶1∶1∶1∶1,其收敛时间为0.28 s;图9(c)中USFRF控制器的支路增益比为k1∶k2∶k3∶k5∶k7=12 ∶3 ∶3 ∶1 ∶1,其收敛时间为0.2 s。 图9 不同控制器的瞬态响应Fig.9 The transient response of different controllers 由图9可以看出,USFRC控制器相较于传统的重复控制器有更快的收敛速率。进一步,通过对比图9(b)和图9(c),说明了根据谐波电流中各次谐波的幅值大小相应地选择合适的增益可以加快控制器谐波收敛速率。 图10给出了稳态响应的谐波电流的频谱图。如图10(a)所示,当加入Xu等研究中的重复控制器时,相较于图8,谐波电流中1次、2次、3次、5次和7次谐波幅值明显下降,下降幅度分别为98.8%(从-26.37~-64.6 dB),96.6%(从-46.96~-76.36 dB),96.4%(从-50.17~-79.22 dB),86.6%(从-56.56~-73.99 dB)以及91.1%(从-55~-76.02 dB)。 图10(b)为加入增益比为k1∶k2∶k3∶k5∶k7=1 ∶1 ∶1 ∶1 ∶1的USFRC控制器后谐波电流的稳态响应频谱图。其中,1次、2次、3次、5次和7次谐波幅值下降幅度分别为99.4%(从-26.37~-71.41 dB),96.9%(从-46.96~-77.03 dB),97%(从-50.17~-80.55 dB),90.6%(从-56.56~-77.12dB)以及94.6%(从-55~-80.39 dB)。 图10(c)为加入增益比为k1∶k2∶k3∶k5∶k7=12 ∶3 ∶3 ∶1 ∶1的USFRC控制器后谐波电流稳态响应频谱图。其中,1次、2次、3次、5次和7次谐波幅值分别下降了99.6%(从-26.37~-74.72 dB),97.1%(从-46.96~-77.67 dB),97%(从-50.17~-80.72 dB),92.8%(从-56.56~-79.45 dB)以及96.6%(从-55~-84.48 dB)。 图10 不同控制器的抑制精度Fig.10 The suppression precision of different controllers 从图10可以看出,通用选择分数阶重复控制器USFRC控制器可以达到较高的收敛精度。进一步,对比图10(b)和图10(c),说明了控制增益的不同选取不会影响控制器最终的收敛精度。 由以上结果可知,针对MSR系统,本文提出的通用选择分数阶重复控制器USFRC控制器可以加快瞬态响应,同时可以达到较高的抑制精度。这种控制器通过建立各个主导谐波的信号内模,采用多个控制器并联的形式在主导谐波处提供无穷增益控制实现了快速高精度抑制主导谐波。 本文对磁悬浮转子系统中主导谐波的快速高效抑制进行了研究,建立了kn+i阶离散周期序列的内模,提出了一种针对低次主导谐波的通用选择分数阶重复控制USFRC。这种控制策略采用并行结构独立抑制各次主导谐波,加快了瞬态响应;为了保证转子在任意转速下的高精度谐波抑制,引入FIR滤波器实现了频率的自适应。同时,本文给出了USFRC控制器的稳定性判据。仿真验证对比结果表明,采用USFRC控制器可以实现快速高精度的谐波抑制效果。



1.2 通用选择性分数阶重复控制器






1.3 稳定性分析


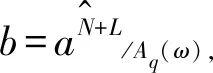
2 仿真结果和分析
2.1 仿真参数

2.2 相位补偿器的设计




2.3 仿真结果和分析





3 结 论
