基于AK-MCS法的主轴系统振动可靠性分析

冯吉路， 孙志礼， 赵 坚， 张 婧， 梁春芳

(1. 天津城建大学 控制与机械工程学院，天津 300384；2. 东北大学 机械工程与自动化学院，沈阳 110819)

随着数控技术的不断发展，高速加工对数控机床主轴系统转速、回转精度和可靠性的要求日益提高，数控机床主轴系统的动力学特性已然成为了当前研究的热点问题[1]。近年来，研究人员采用传递矩阵法[2]、有限单元法[3-7]和集中参数法[8-10]等主轴动力学建模方法对主轴系统动态特性进行了大量的研究，主要分析了相关因素对主轴固有频率和振幅的影响。主轴轴承滚子与滚道之间非连续、非光滑接触会使得主轴系统产生非线性振动，进而影响主轴系统的动力学特性。特别在轴承滚子与滚道之间留有间隙时，该间隙会在轴承非线性Hertz接触力和主轴非平衡力的作用下，引起主轴系统的非线性分岔和混沌现象，进而可能导致主轴系统振幅过大或系统失稳[11-12]。

机床主轴系统动力学性能可靠性是设计工作者应该重点关注的问题，它是衡量机床整机性能的主要指标，会受到轴承和主轴材料的刚度和阻尼等诸多参数的影响。在这些设计参数变化的情况下，主轴轴端轴心的振动幅值必然会发生变化。当振动幅值超过设计指标时，就会引起设计失效，而不发生设计失效的概率，可以被定义为主轴振动幅值的可靠度。由于主轴动力学模型是强非线性系统，采用一般的可靠性分析方法必然会增加计算工作量，延长设计周期。为了解决此问题，近年来研究人员提出了各种方差缩减技术，如分层抽样[13]、重要抽样[14]、控制变量[15]等方法。虽然上述方法能够减少样本数量，但是很难满足强非线性系统的实际工程需求。

鉴于上述问题，建立了考虑弹性主轴刚度、阻尼和滚动轴承非线性接触力的十自由度数控车床主轴非线性振动分析模型。利用Runge-Kutta数值积分法对数控车床主轴-滚动轴承系统的振动微分方程进行了数值求解。采用Kriging模型和Monte Carlo法相结合的方法计算了主轴动力学性能可靠度。该研究为设计工作者进行机床主轴系统动力学性能可靠性设计提供了理论基础。

1 主轴-轴承系统模型

1.1 滚动轴承接触力模型

轴承的内、外圈滚道是与滚动体相接触的，在每一个接触点，由于是Hertz接触，滚动体与滚道之间的接触变形会产生一个具有非线性特性的恢复力[16]

fθj=kn(rθj)n

(1)

式中：n为常数，对于球轴承，n=3/2；rθj为滚动体j在角位置为θj处的接触变形量；kn为接触刚度。在任意时刻，第j个滚动体在接触点上的弹性变形取决于滚动轴承质心的位移和轴承的初始游隙

rθj=xsinθj+ycosθj-γ

(2)

式中：γ为轴承的初始游隙，将式(2)代入式(1)中，由轴承滚动体接触力的非负性可得

(3)

总的接触力是每一个滚动体接触力的总和，考虑到接触阻尼cn的影响，可以得到在x和y方向上滚动轴承轴承总接触力

(4)

由式(4)可知，轴承的接触力与主轴的轴心轨迹有紧密的联系，并且滚动轴承的刚度具有时变性，可能导致主轴-滚动轴承系统运转过程中出现混沌响应。根据文献[17]计算了机床主轴系统中的前后轴承组的等效总接触刚度系数分别为kn1=3.145×109N/m3/2，kn1=2.178×109N/m3/2，轴承组的总接触阻尼大小和刚度系数成比例，为cn=0.25×10-5kn；对于轴承游隙，假设成组轴承中每个轴承的游隙完全相同，前后轴承组的游隙分别为r1=53.65 μm，r2=19 μm。

1.2 主轴-轴承系统动力学模型

典型数控车床主轴系统主要由主轴、滚动轴承、卡盘、带轮以及定位元件等组成，其中主轴系统前、后端轴承组分别采用NSK 7016A5(DBD) 组合和 7015C (DB)组合的形式，如图1所示。NSK 7016A5和7015C的轴承结构参数如表1所示。

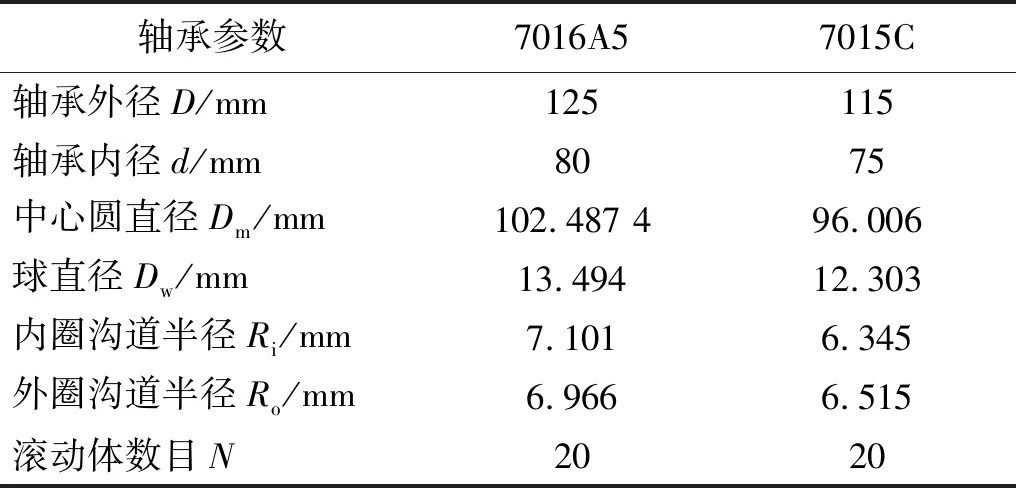
表1 角接触球轴承的原始参数

图1 典型数控车床主轴-轴承系统Fig.1 A typical spindle-bearing system of the CNC lathe

分析数控车床主轴系统零部件分布可知，该系统的质量主要位于主轴的两端以及前、后轴承组之间。为了便于分析，研究中采用张伟刚等所使用的集中质量法对国产数控车床主轴系统进行了简化，简化系统由5个集中质量单元和4个弹性轴段组成，考虑集中质量单元在X和Y方向的平动，可将该主轴-滚动轴承系统简化为十自由度系统，如图2所示。其中，非线性轴承力和转子的偏心力为系统的激励。简化后主轴系统的动力学微分方程为

图2 机床主轴-轴承系统力学简化模型Fig.2 Simplified mechanical model for machine tool spindle-bearing system

(5)

式中： 主轴简化后的集中质量分别为m1=9.35 kg，m2=4.61 kg，m3=8.59 kg，m4=1.77 kg，m5=13.76 kg； 集中质量间轴段的刚度系数为k12=k23=k34=k45=1.41×108N/m，阻尼系数为比例阻尼，其中c1=αk1，c2=αk2，α=0.001/ω，e=10-5m。

2 Kriging模型与学习停止条件

2.1 Kriging模型

Kriging模型[18]是一种半参数化的插值模型，不需要给出状态函数的具体形式，这样可以使模型的预测精度不受假定函数形式的影响。另外，Kriging模型可以应用于强非线性的问题。Kriging模型表示为

g(x)=fT(x)β+z(x)

(6)

式中：fT(x)β为回归模型，β为回归系数向量，f(x)为随机变量x的多项式函数，通常可以取固定值，其取值的大小并不影响模型的近似精度。

z(x)是随机过程函数，反映局部偏差的近似，它的均值μ是零，方差是σ2，协方差表示为

cov(z(xi),z(xj))=σ2R(xi,xj)

(7)

式中：R(xi,xj)为带有参数θ的关于样本点xi和xj的相关函数，模型的准确性取决于随机过程z(x)，相关函数通常选用高斯相关方程，其表达式为

(8)

(9)

给定训练样本集合S={x1，x2，…，xns}，计算相应的实际功能函数响应值，将其用向量形式表达为

Y=[g(x1),g(x2),…,g(xns)]T

(10)

β和σ2的估计值为

(11)

(12)

式中：N0为向量的维数。

通过Kriging模型，得到待测点x的预测响应值为

(13)

式中：f=[f(x1),f(x2),…,f(xns)]T；r(x)=[R(x,x1),R(x,x2),…,R(x,xns)]T。

Kriging方差为

(14)

式中：u(x)=fT(x)R-1r(x)-f。

2.2 学习函数与停止准则

为了使Kriging模型不断优化，实现自动查找和增加最合适的训练样本，定义学习函数U(x)为

(15)

一般而言，可以选择U(x)取值最小的样本点作为最合适的训练样本点。为满足进一步分析的需求，还需要定义停止学习的条件。由于学习函数U(x)与Cox和John提出的用于优化的具有比较小置信区间的函数具有一定联系，根据相关研究，本文给出了相应的停止学习准则

(16)

式中：A为将要分类的样本集。在判断这些样本点所在区域时发生错误的概率为Ф(-2)=0.023。通过建立学习函数和相应的学习停止准则，可以保证在不断更新后的Kriging模型具有更好的精度。

3 主轴振动可靠性的计算流程

根据建立的十自由度振动微分方程求得了主轴转速为n=0～4 000 r/min时系统轴端轴心的最大振动幅值，并使用Kriging模型构建了样本数据与响应值之间的关系。采用AK-MCS主动学习方法进行主轴轴端振动可靠度计算，计算流程如图3所示。具体计算步骤如下：

图3 AK-MCS算法流程图Fig.3 Flow chart of the AK-MCS

步骤1由本文“4.1”节可知，主轴系统轴端振动幅值的大小会受到主轴前、后轴承组的轴承接触刚度和游隙的因素的影响。假设设计变量服从正态分布，根据轴承厂提供的轴承设计参数，结合主轴系统中轴承组受载情况，应用赫兹接触理论确定的设计变量的均值。各变量的均值和标准差如表2所示，其中x1为主轴系统前轴承组的等效接触刚度、x2为后轴承组的等效接触刚度、x3为前轴承组单个轴承的径向间隙、x4为后轴承组单个轴承的径向间隙，其余参数均为定值。根据Monte Carlo方法，在随机变量的设计空间中生成的n组随机样本，称为候选样本点，用S来表示，这些候选样本点不需计算其实际功能函数响应值，它们会被应用到之后构建Kriging模型时利用学习函数自动查找和增加最佳候选样本点的过程当中，只有被选为最佳候选样本点时，才需要计算该最佳候选样本点的实际功能函数响应值。

表2 主轴系统的设计变量

步骤2采用拉丁超立法抽样方法生成初始训练样本点，用S1来表示这些样本点需要通过仿真或计算得到其实际功能函数响应值，并用Y1来表示。初始训练样本点中样本点的数量一般选取的较少，会在之后的学习过程中不断地增加最佳候选样本点，不断地优化模型。

步骤3利用训练样本点S1和实际功能函数响应值Y1， 应用MATLAB中的DACE工具箱，构建Kriging模型，Kriging模型的回归模型部分选用一次多项式，相关函数采用高斯相关函数。

步骤4利用构建的Kriging模型，计算候选样本点S中所有样本点的预测值和预测方差，并计算这些候选样本点的学习函数值，并挑选候选样本点中学习函数值中最小的样本点，作为最佳候选点。

步骤5如果最佳候选点的学习函数值满足学习停止条件，则构建Kriging模型的主动学习过程结束，否则，将最佳候选点加入到训练样本点中，并计算其实际功能函数响应值，转到步骤3，构建新的Kriging模型。

步骤6如果主动学习过程结束，采用当前的训练样本点及其实际功能函数响应值所构建的Kriging模型，此时的Kriging模型为优化后的比较精确的模型，运用Monte Carlo方法计算失效概率Pf以及可靠度Pr。

4 结果与分析

4.1 参数变化对主轴轴端振幅的影响

数控车床主轴系统是一个具有强非线性特征的滚动轴承-主轴系统。主轴系统的轴端动态响应会决定机床工作过程中的加工精度，而轴端的动态响应主要会受到前、后轴承组的接触刚度和轴承游隙等相关参数的影响。

图4为n=6 500 r/min时主轴前端轴心随前、后轴承组的总接触刚度以及前、后轴承游隙变化的稳态响应分叉图。由图分析可知，轴承接触刚度和轴承游隙对主轴轴心振幅会产生影响；当其它参数保持不变时，前轴承组总接触刚度仅仅在[1.15×109N/m1.5,1.2×109N/m1.5]内变化，会导致主轴轴端响应出现跳跃现象，说明此时系统出现了多个周期吸引子；相比之下，后轴承组的接触刚度较低时，很容易引起系统的拟周期或者混沌运动状态，但是当后轴承刚度增大到一定程度时，刚度几乎不会引起主轴前端轴心振动幅值的变化。由图4(c)和图4(d)可知，当其它参数不发生变化时，前、后轴承游隙增加到一定程度时，将不会对主轴轴端的振动幅值产生影响。

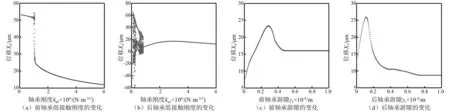
图4 n=7 500 r/min时主轴前端轴心随相关参数变化的分叉图Fig.4 Bifurcation diagram for the axis at the front of the spindle with changed parameters when rotational speed n=7 500 r/min

4.2 主轴轴端振动可靠性计算结果

采用拉丁超立方抽样抽取60个样本点，建立初始Kriging模型，由学习函数进行样本数据更新，当满足停止学习条件时，得到最终的Kriging模型和系统的可靠度。为了验证方法本文提出方法的有效性，应用Monte Carlo抽样方法抽得5×104组样本数据，并将其带入振动微分方程式(5)，可分别求得不同样本点的轴端轴心的最大振动幅值。假设轴心许用振动幅值为15 μm，此时，可得到了极限状态函数的样本历史和概率直方图，如图5和图6所示。分析图6可知，极限状态函数值g(x)的分布图接近正态分布概率函数曲线，比较光滑且没有间隙，表明抽样次数足够多。表3为本文提出方法和Monte Carlo法的可靠度计算结果。由于主轴系统是典型的强非线性系统，而很多可靠度计算方法在针对强非线性系统进行求解时会失效。通过对比Monte Carlo法和本文所使用的方法，说明了本文提出的方法在求解强非线性系统可靠度的有效性，也论证了该方法的高效性。

表3 不同方法的计算结果

图5 g(x)的样本历史Fig.5 Sample history of g(x)

图6 极限状态函数g(x)频率直方图Fig.6 Frequency histogram of limit state function g(x)

5 结 论

(1) 采用集中质量法对国产数控车床主轴系统进行了简化，建立了考虑主轴刚度、阻尼、偏心质量和成组滚动轴承非线性接触力的十自由度非线性振动模型。

(2) 主轴系统后轴承组接触刚度较低时，很容易引起系统的拟周期或者混沌运动状态，且前后轴承组轴承游隙匹配合适有利于减小主轴振幅。

(3) 通过对比Monte Carlo和AK-MCS法计算的可靠度结果可知，AK-MCS法计算效率高，收敛速度快，特别适用于解决强非线性隐式复杂问题，且有效提高数控机床主轴可靠性设计的效率。