高坝泄流诱发闸门伴生振动的双调谐TMD减振方法研究

梁 超， 练继建， 张金良

(1. 黄河勘测规划设计有限公司，郑州 450003；2.河海大学 水利水电学院，南京 210098；3. 天津大学 水利工程仿真与安全国家重点实验室，天津 300350)

近30年，我国水利水电工程的建设规模和难度均局世界首位，泄洪携带的巨大能量以及高速水流的复杂特性，使得泄洪振动问题十分突出。高坝泄流诱发的振动问题主要包括水工结构振动安全和周边环境振动安全两个方面。其中，水工结构振动安全是工程水力学领域的传统研究课题，并以闸门在泄流过程中受到的不利振动影响为最。国内外学者以理论分析和模型试验为主要手段，对闸门流激振动的发生机制进行了大量研究[1-12]，但所得到的结论只在特定的条件下适用。一般认为闸门的振动可能由以下机制导致，即：涡激振动、流量脉动、滚轮受力不均导致的颤振、胸墙空腔激振、参数共振和空化振动等。由于水流荷载特性，水流-闸门耦合作用机制，以及闸门复杂阻尼特性等方面仍缺乏深入而明确的认识，实际中由于振动而导致闸门无法正常使用甚至破坏失稳的案例时有发生[13]。文献[14]中将水工闸门的动力稳定和振动控制归纳为未来闸门研究聚焦的七大方向之一。而且，近年来原型试验发现的闸门爬行振动和伴生振动等特殊振动形式均具有能量集中、频率稳定的特点，为动力学减振措施的应用提供了极为有利的条件[15]。

目前，动力学减振措施在土木、船舶和机械等领域已有了较为广泛的应用并取得了良好的效果[16]，但在闸门振动控制方面的应用仍是空白。其原因可能是由于闸门的流激振动机制过于复杂，从而使得系统本身的不确定性限制了控制器的应用。文献[17-18]提出利用磁流变阻尼器对弧形闸门流激振动进行振动控制，并研究了LQ(Linear Quadratic)和遗传优化模糊两种半主动控制策略，为闸门减振研究提供了新的方向。但该研究仅限于数值模拟，且磁流变阻尼器作为一种新型的非线性吸振器，其理论模型、实际性能和控制策略均有待实践检验。因此，本文考虑近年来原观试验中发现的闸门伴生振动，根据对于具有不确定性和外部干扰的模型有更强适用性的鲁棒控制理论，采用基于H∞性能目标设计的双调谐TMD(Tuned Mass Damper)减振措施，一方面对闸门的优势频率振动进行有效衰减，同时在更宽的频带范围内产生抑振效果，避免由于流固耦合机制的复杂性导致削弱伴生振动的同时发生其它机制的强烈振动。基于主体结构-双调谐TMD的振动控制方程，推导了双调谐TMD参数优化设计的目标函数和约束条件，并利用动力特性与实际情况相似的简化模型计算了双调谐TMD的参数。为了验证上述减振方法的效果，将优化设计的双调谐TMD安装于实际闸门结构并进行数值计算，结果表明所提出的方法能够有效衰减闸门的伴生振动，保障闸门的安全和正常运行。

1 原型观测中的水工闸门伴生振动现象

闸门泄流振动问题在很早之前就被研究人员所关注，但由于问题的复杂性，其振动机制一直没有明确的结论。一般而言，闸门流激振动与底缘型式、泄流水头、过流面积、闸门两侧流态和结构自身的动力特性等诸多因素有关，通常随着过流流速的增大，更容易发生较为明显的流激振动现象。然而，在2014年汛期对某工程闸门泄流运行动力学监测中，发现了闸门的伴生振动现象。其表现为振动在闸门全关时达到最大，随着闸门的开启，虽然水流荷载作用于闸门底缘，但其振动却逐渐减小，与传统的闸门流激振动现象具有显著差异。伴生振动的时频特性、分布规律、随开度的变化情况以及诱发机制的简要分析如下所述。

1.1 原型观测工况

该工程的挡水建筑物采用混凝土双曲拱坝，坝身设4个表孔、5个深孔，表中孔泄洪功率超过10 000 m3/s，坝后采用水垫塘消能，消能水头超过230 m。工程首次蓄水至正常蓄水位时，进行了闸门动力学原型观测，观测工况如表1所示。

表1 某工程闸门振动原型观测试验工况

1.2 深孔闸门振动

坝身深孔为一段有压短管，下泄水流一般呈急流状态，工程界目前对急流脉动荷载特性的研究较少，已有的研究表明，急流脉动荷载可能由较高频率的分量组成。图1给出了中孔闸门(3#)的振动加速度测点布置图，图上每一个测点处均安装三向振动传感器。

图1 中孔闸门(3#)传感器布置图Fig.1 Sensor arrangement of 3# mid-level orifice gate

图2中给出了工况1条件下3#中孔闸门的振动加速度均方根和优势频率。多数情况下，z方向(支臂垂向)振动比x方向(支臂横向)和y方向(支臂轴向)振动更加强烈，且振动主频多为26.2 Hz。由于工况1中只有3#中孔闸门开启，因此认为中孔闸门振动是由其本身下泄水流作用于闸门底缘而引起的。基于实际原型观测结果和各中孔闸门下泄水流条件的相似性，2#和4#中孔闸门全开时的振动规律和时频域特性与3#中孔闸门振动情况几乎相同。一般地，水流脉动优势频率较低，不易诱发结构的高频振动。但水工闸门的高频振动现象较为普遍[19-22]，可能是由于频率较高的急流脉动荷载和水流-闸门耦合振动机制而导致。

图2 工况1条件下3#中孔闸门各测点不同方向加速度时程的均方根和主频Fig.2 Root mean squares and dominant frequencies for acceleration histories of measuring points on 3# mid-level orifice gate in different directions in case 1

1.3 表孔闸门的“伴生”振动现象

坝身表孔为WES溢流堰，堰宽11 m，闸墩高度12 m。在工况5和工况6中，闸门底缘与下泄水流直接接触；在工况7和工况8中，闸门底缘与下泄水流脱离，此时闸门不受水流荷载作用。图3给出了3#表孔闸门的测点布置图，图3上每个测点均安装三向振动加速度传感器。

图3 表孔闸门(3#)传感器布置图Fig.3 Sensor arrangement of 3# crest orifice gate

图4和图5给出了3#表孔闸门的振动加速度均方根和主频。如图4所示，表孔闸门关闭时振动最大，随着闸门开度的增加，其振动明显减小，而当闸门底缘完全脱离水面后(工况7和工况8)，再增加开度其振动保持不变。

图5给出了3#表孔闸门振动主频，可知绝大多数主频在27.5～28.5 Hz，图中高于40 Hz的振动频率可能是由于闸门附属结构(如人行楼梯，扶手)振动，传感器信号失真，通勤车辆以及其它部位施工造成的信号干扰所致。

图4 不同工况下3#表孔闸门振动加速度均方根Fig.4 Vibration acceleration root mean squares of 3# crest orifice gate under different cases

图5 各工况下3#表孔闸门振动优势频率Fig.5 Vibration dominant frequencies of 3# crest orifice gate under different cases

注意到表孔和深孔闸门振动频率较为相似，且二者在空间上较为接近，所观察到的表孔闸门振动属于中孔闸门振动诱发的伴生振动现象。梁超对闸门的伴生振动机制进行了详细研究，简要而言，表孔闸门开度由0%增加到25%时，从中孔闸门经由坝体到表孔闸门的振动传播路径由于表孔闸门底缘与WES堰顶的脱离而被部分地隔断，因此表孔闸门振动减小；闸门开度由25%增加到50%时，过流面积增加和流速减小导致的水流脉动荷载的减小，使表孔闸门振动进一步减小；闸门开度由50%增加到75%时，闸门底缘与下泄水舌脱离，不再受到水流荷载，因此闸门振动继续减小；闸门开度由75%增加到100%时，由于闸门所受到的外加荷载几乎不发生变化，因此两种工况下闸门的振动强度几乎相同。

2 被动减振方法在闸门伴生振动中的应用

2.1 基于H∞性能目标的双调谐TMD理论模型

由“1.3”节的分析可知，表孔闸门的伴生振动是由中孔闸门振动经由坝体及闸墩等结构传递至表孔而产生。一方面水流在闸门振动中所起的作用较小，从而在传统闸门流激振动中起重要作用且机理不明的流固耦合机制不必考虑；另一方面应避免由于流固耦合机制的复杂性导致在衰减伴生振动的同时产生其它机制的强烈振动。

由于伴生振动能量集中、频率稳定，且不必考虑流固耦合机制，因此可以利用被动式减振器进行振动控制。为了在更宽的频带范围内对振动进行衰减，避免产生其它机制的强烈振动代替伴生振动成为振动的主要形式，本文采用多个双调谐TMD，以H∞鲁棒控制性能为目标函数，除对振动优势模态进行减振外，同时也考虑对闸门振动基频进行控制。一般而言，结构基频对应模态的振动参与程度较高，且对基频的减振通常对高频的振动同样具有衰减作用[23]。在综合考虑一阶模态和振动优势模态减振效果的基础上，进行双调谐TMD参数设计。

如图6所示，为利用双调谐TMD对主体结构某阶模态进行减振分析的简化力学模型，其振动基本方程可以表示为

(1)

(2)

(3)

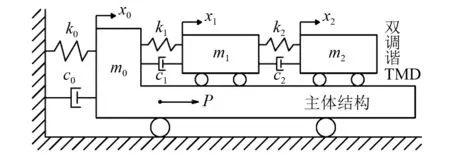
图6 主体结构-双调谐TMD系统简化模型Fig.6 Simplified model of primary structure-double TMD system

式(1)～式(3)可以表示为矩阵形式

(4)

式(4)可以简化表示为

(5)

式(5)中的各参数表达式为

在式(5)的基础上构造状态空间方程

(6)

式(6)中的各参数表达式为

式中：u为反馈控制力；XT为反馈控制增益矩阵，包含需要进行优化设计的双调谐TMD阻尼和刚度参数。

关于控制输出向量z的表达式可表示为

z=D1x+Ew+D2u

(7)

式中:z可根据减振目标的需要选择为结构的位移、速度或加速度等响应；D1，E和D2分别为恰当维数的矩阵。

为了后续分析的方便，将式(6)和式(7)改写为

(8a)

z=Dsx+Esw

(8b)

式(8)中的各参数表达式为

As=A1+A2XT;Bs=B；

Ds=D1+D2XT;Es=E

控制输出向量z的L2范数的平方为

(9)

干扰输入w的L2范数的平方为

(10)

令包含未知参数矩阵XT的系统传递函数矩阵为T(XT)，从而系统的H∞范数为

(11)

式中:sup为系统L2范数增益对所有干扰输入w的上界。定义正实数γ∞为系统H∞范数的极小值，作为系统的H∞性能目标，式(12)成立

‖T(XT) ‖∞≤γ∞

(12)

为了求解式(12)，可以引入李雅普诺夫函数

V(q)=qTPq

(13)

式(13)具有零初始条件，且矩阵P为对称正定矩阵。

根据李雅普诺夫系统稳定性判定理论，可得

(14)

因此，不等式成立

(15)

式中：时间t在0～∞内变化。

根据schur补性质，并作适当变化[26]，可得线性矩阵不等式

(16)

式中：Q为对称正定矩阵，且Q=(P/γ∞)-1。

注意到式(16)为不确定性系统的线性矩阵不等式，其求解较为困难，本文在下述内容中以闸门的简化模型为基础，通过试算法求解式(16)，并考虑对一阶模态和振动优势模态的综合减振效果，进行双调谐TMD的参数优化设计。

2.2 双调谐TMD的布置方案

研究表明，在主体结构上合理布置多个TMD起到的减振效果比采用与多个TMD总质量相同的单个TMD的减振效果更好。而且，TMD应安装在目标减振模态振型向量的绝对值最大值对应的节点处。对于本文所针对的闸门体型，上述原型观测得到的振动总体表现和数值分析得到的各模态振型都表明其振动最大值位于闸门的支臂处。因此，在后续分析中主要考虑将双调谐TMD布置于闸门支臂上的振动较大处。

3 双调谐TMD参数优化设计

3.1 闸门简化模型的建立

由于实际闸门结构的复杂性，为了方便进行双调谐TMD的设计，需要建立闸门的简化模型，图7和图8给出了闸门的简化和实际模型。为了保证基于简化模型设计的双调谐TMD对于实际模型也具有良好的减振效果，简化模型在目标减振模态应与实际模型具有相似的频率和振型特征，这里我们主要关注一阶振动模态和振动优势频率模态。

图7 闸门简化模型Fig.7 Simplified gate model

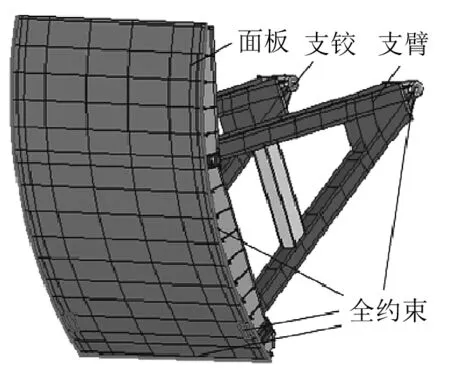
图8 闸门实际模型Fig.8 Actual gate model

表2和表3分别给出了简化和实际闸门模型的模态频率和振型特征。由于自由度的减少，简化模型不可避免地丢失了大量振动模态，但是所关注的1阶模态(18 Hz左右)和振动优势频率模态(27 Hz左右)的频率和振型特征均与实际模型相仿。因此认为首先基于简化模型设计双调谐TMD，然后将设计好的双调谐TMD应用于实际模型可以起到减振效果。需要指出的是，为了使简化模型与实际模型具有相似的动力学特性，对图7中的梁单元赋予了不同的截面属性，双调谐TMD参数设计所用到的刚度和质量矩阵等参数可以在ANSYS等数值软件中方便地提取。

表2 闸门简化模型的动力特性

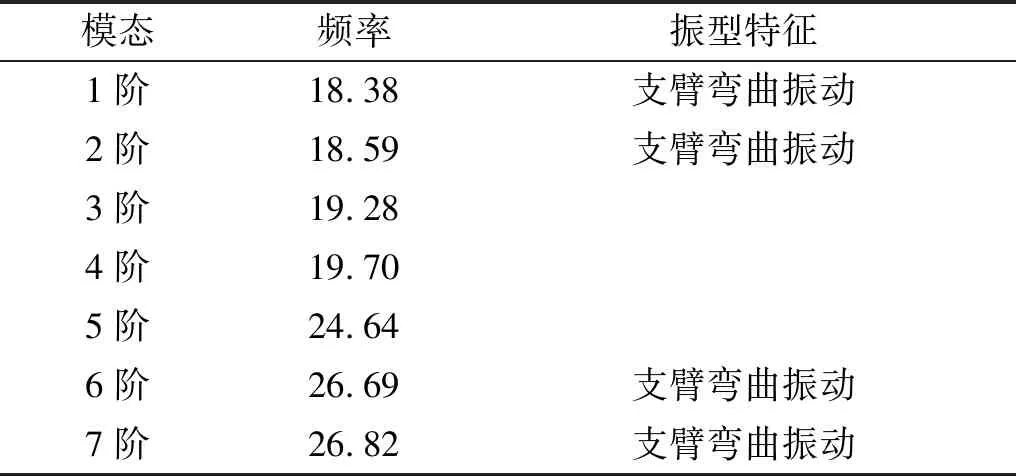
表3 闸门实际模型的动力特性

3.2 基于简化模型的双调谐TMD参数优化设计

如上所述建立了闸门的简化模型，并保证其在目标减振模态上与闸门实际体型具有相似的动力学特性。由于双调谐TMD的刚度和阻尼均未知，因此式(16)属于具有不确定性的线性矩阵不等式，即使利用Matlab等数值计算软件，其求解也较为困难。实际上，对目标模态进行减振，一般要将TMD的自振频率调谐至对应模态的振动频率。在主体结构不具有过大的阻尼时，频率调谐条件对于经典控制理论和鲁棒控制理论都具有较好的适用性[27]。为了增强减振效果，在闸门支臂模态振动较大位置处分别布置8个双调谐TMD，并将双调谐TMD的总质量取为主体结构质量的0.01倍。因此，计算可得单个双调谐TMD的质量和刚度参数分别为：m1=180 kg，m2=20 kg，k1=2.85×106N/m，k2=4.2×105N/m。对应的，双调谐TMD的两阶自振频率分别调谐至18.11 Hz和26.90 Hz，与主体结构的一阶和振动优势频率极为接近。

以上分析合理地确定了双调谐TMD的质量和刚度，因此双调谐TMD的参数设计转化为对其阻尼c1和c2的优化设计。利用Matlab自带的LMI工具箱，以式(16)为求解对象，考虑矩阵变量Q的正定性，并以正常数γ∞作为优化目标，在阻尼c1和c2初始值取为瑞利阻尼(质量系数α=6.800 2，刚度系数β=3.536 2×10-4)的条件下，分别乘以1～100的放大倍数，分析不同阻尼的双调谐TMD的减振效果。如图9和图10所示，减振效果随阻尼c1和c2的不同而呈现较为复杂的变化情况。对于结构一阶模态而言，适当增大阻尼对减振效果具有积极作用，随着阻尼的持续增加，其减振效果逐渐变差；对于结构的振动优势频率模态，当阻尼c1在瑞利阻尼初始值的基础上放大6倍时，能够保持较好的减振效果。综合考虑两阶目标减振模态的减振效果，将阻尼c1和c2设置在初始瑞利阻尼的基础上分别放大6倍和50倍。

图10 双调谐TMD在不同阻尼下对振动优势模态的减振效果Fig.10 Vibration reduction effect of double TMD with different damping on the dominant vibration mode

图9 双调谐TMD在不同阻尼下对一阶模态的减振效果Fig.9 Vibration reduction effect of double TMD with different damping on the first vibration mode

4 减振效果评价

4.1 实际闸门模型和双调谐TMD的布置

采用以上分析中所确定的双调谐TMD优化设计参数，并将TMD布置于实际闸门有限元模型中支臂振动较大、约束较弱的部位，如图11所示。由原型观测数据可知，表孔闸门支臂垂向振动明显大于支臂横向和轴向振动。因此，为了简化分析，文中所采用的双调谐TMD主要考虑垂直于支臂的制振方向，质量块的行程均取为0.5 m。双调谐TMD中的质量块、刚度和阻尼分别由ANSYS中的MASS21和Spring-damper14单元模拟。数值模型在支铰和启闭杆支撑点处采用全约束，并在门叶左、右和底缘边缘处输入外加荷载，以考虑表孔闸门伴生振动最大工况下(表孔闸门全关)的动力响应。

图11 双调谐TMD在实际闸门有限元模型上的布置Fig.11 Double TMD arrangement on the actual gate finite element model

4.2 动力响应分析

图12给出了输入的加速度荷载时程，由于直接激励于闸门左、右和底缘的坝体振动数据的缺乏，文中采用深孔闸门的振动加速度近似代替表孔闸门所受的激励。并提取图11中A点的归一化位移响应进行分析，结果如图13所示。相对于无TMD系统，安装有双调谐TMD的闸门振动响应最大值衰减了44.4%，表明所提出的减振方法能够起到较好的减振效果。

图12 输入加速度时程Fig.12 The input acceleration history

图13 模型中A点的位移响应Fig.13 Displacement response of point A in model

图14和图15分别给出了相同位置测点的无TMD系统和双调谐TMD系统的位移响应时程对比。结果表明，相对于无TMD系统，安装有双调谐TMD的闸门振动响应最大值分别衰减了50.8%和48.0%，从而进一步验证了该方法的有效性。

图14 模型中B点位移响应对比Fig.14 Displacement response comparison of point B in model

图15 模型中C点位移响应对比Fig.15 Displacement response comparison of point C in model

5 结 论

本文基于闸门伴生振动能量集中、频率稳定的特点，采用双调谐TMD减振措施，建立了振动控制方程；基于H∞鲁棒控制设计目标，推导了闸门-双调谐TMD体系参数优化设计的目标函数和约束条件；并对动力特性与实际相似的简化模型进行了参数优化设计；将优化设计的双调谐TMD安装于实际闸门结构进行动力分析。数值结果表明，相对于不安装减振措施的闸门结构，所提出的减振方法能够将闸门的伴生振动衰减40%～50%，减振效果较为显著。

必须指出的是，本文所提出的减振方法在以下方面还存在不足：

(1)数值分析中双调谐TMD的制振方向为支臂垂向，即只考虑了在垂直于门叶荷载的作用下，幅值较大的支臂垂向振动的减振效果，而实际情况中闸门在受到垂直于门叶的荷载作用的同时也会受到其它方向的荷载。同时闸门支臂在垂向振动的同时也可能产生较大的横向和扭转振动，在进行双调谐TMD参数优化设计时应予以综合考虑。

(2)双调谐TMD的参数设计是依据简化闸门结构而设计的，由于简化闸门结构和实际闸门之间的差异性，所提出的双调谐TMD虽然具有一定的减振效果，但并不是最佳参数设计。

(3)由于不确定性的线性矩阵不等式较难以求解，文中作了一定的简化考虑，因此对于具有不确定性的线性矩阵不等式的有效求解方法是进一步研究的方向。

(4)由流固耦合作用机制为主导所产生的闸门振动的减振方法亟需进一步研究。