发射装置中振动控制点选择方法分析

2012-09-18张汉伟盛德兵周志卫

重庆理工大学学报(自然科学) 2012年12期

张建，张汉伟，盛德兵，周志卫

(1.郑州飞机装备有限责任公司弹射技术实验室，郑州 450005;2.中国人民解放军驻124厂军事代表室，郑州 450005)

目前的实物振动试验周期长、成本高，具有一定的风险性，还伴随着强烈的噪声。而虚拟振动试验可多次反复地再现整个试验过程，使研发人员在产品开发中不断迅速修正设计，从而大大减少昂贵而费时的物理样机制造及实物试验过程，缩短研制周期，提高产品的研制质量［1－4］。

振动试验主要通过监测控制点上的响应来调整所施加的振动激励，以使产品整体响应符合规定要求，保证试验的有效性，因此，控制点的选择便显得尤为重要。振动试验标准只是对控制点的选择给出了一个粗略的范围，在以往的实物试验中，往往只依据标准，通过经验判断来布置控制点。然而规定的试验控制点范围较宽，上述通过人工判断布置控制点的方法存在较大的盲目性，很难找到一个准确的点来保障试验的公正性要求。这种控制点选择上的盲目性可能会导致2种极端情况:如果控制点选在了响应偏小的位置，随着激励的不断增加，容易造成试件整体响应过大，出现过试验现象，甚至损坏产品;反之，如果选在了响应偏大的位置，则试件整体响应达不到要求，出现欠试验现象。为此，本文提出了采用虚拟试验技术来模拟振动试验的方法，对实物振动试验的控制点选择进行设计［5－7］。

本文对某悬挂发射装置进行研究。首先利用SolidWorks对三维实体骨架模型进行构建，并做必要的简化，如将无关紧要的倒角、边界等去除，尽量减少模型的曲面、短小截面，形成新的平滑模型，以便在目前的硬件技术条件下进行计算［8－9］。然后将模型导入MSC.NASTRAN的前处理平台划分网格，再在产品上接口的2个孔内施加激励，同时在产品下接口的4个孔内施加全约束。假设悬挂物质量足够大，使得全约束条件成立。然后进行模态和频率响应计算。最后通过分析计算结果，在产品施加激励和约束的位置附近寻找适合振动试验的控制点。

1 虚拟振动试验分析模型准备

谱分析是模态分析的扩展，用于计算结构对地震及其他随机激励的响应。本文将用响应谱分析方法进行振动试验的模拟。

1.1 分析模型构建

在简化过程中既要忽略对最终结果的分析误差，又必须满足计算软件的需求。利用SolidWorks建立某产品骨架的三维实体简化模型，如图1所示。

图1 骨架三维实体简化模型

将简化过的SolidWorks文件转化为.X_T文件，并导入 MSC.NASTRAN，划分网格，如图 2所示。

图2 骨架模型网格模型

1.2 建立频率谱和工况

建立频率谱，范围为20～500 Hz，共分为400段，功率谱密度为1 g2/Hz，利用PCL语言设置，如图3所示。

图3 利用PCL语言设置的频率谱

1.3 施加激励和约束

在产品上接口的2孔内施加向下的5000 N压力谱作为模拟振动试验的激励条件，此激励为依赖频率谱的函数。在产品下接口的4个孔内施加全约束，以模拟质量很大的悬挂物，施加位置如图4所示。

图4 激励和约束的施加位置

1.4 定义材料属性及物理特性

材料按照钢的属性定义:弹性模量E=2.06×1011N/m2，泊松比 υ =0.3，密度 δ=7800 kg/m3，阻尼ζ=2%。

1.5 分析计算的参数设置

计算参数设置:频率范围为20～500 Hz，共分为400段，在阻尼ζ=2%的情况下使得振幅有所收敛。设置完成后将模型提交计算。

2 计算结果分析

通过以上计算，可以得到产品骨架上各点的响应值、应变分布、应力分布等，应用这些数据能很好地分析振动试验中各节点情况，从而更合理地选择试验所需要的控制点分布位置。

2.1 响应谱分布

经计算可得，频率为20～500 Hz时，最大响应值均出现在下接口最右边孔的右侧偏上，距离孔心大约20 mm的位置，其值在此频率区间线性增加，在500 Hz时达到2770 MPa。最小响应值出现在位于骨架最左端节点7607位置，其值在500 Hz时为2.45 MPa，可忽略，如图5所示。

节点7607和节点7762的响应值随频率变化分布如图6所示，频率区间为20～500 Hz。

为了更直观地分析响应值的分布规律，随机选择另外5个点作为参照，如图7所示。

图5 500 Hz频率下各点响应云纹图

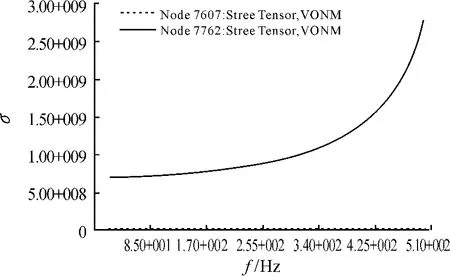
图6 最大响应值和最小响应值随频率变化分布

图7 随机选择的节点位置

得到这些节点的响应值随频率变化的分布，如图8所示，可以看出所选取的节点响应值大小均介于节点7762和节点7607的响应值之间。

图8 随机节点的响应值随频率变化分布

为了更直观分析计算结果，选取参考频率为340 Hz，得到各节点响应值，如表1所示。

通过以上分析，可以得到任意节点在不同频率下的响应值，据此能判断出产品上激励和约束施加位置附近节点的响应值，从而寻找到合适的控制点，以满足试验要求。

2.2 利用响应分布选择控制点

为了合理地选择控制点的位置，在施加激励和约束的各接口孔附近选取几个参考点，比较其响应值分布。

2.2.1 位于左边上接口附近节点的响应值计算

在左边上接口施加激励的孔附近选取节点，如图9(a)所示。

得到这些节点响应值随频率变化分布，如图10所示。最大响应值出现位于上接口左孔的右侧偏下，距离孔中心大约55 mm的节点1290，最小响应值出现在位于上接口左孔的左侧偏下，距离孔中心大约40 mm的节点7182处，如图9(b)所示。

选取参考频率为340 Hz，得到各节点响应值，如表2所示。

图9 左激励附近选取节点的位置

图10 左激励附近节点响应值随频率变化分布

表1 340 Hz频率下随机节点的响应值 Pa

表2 340 Hz频率下左激励附近节点的响应值 Pa

2.2.2 位于右边上接口附近节点的响应值计算

在右边上接口施加激励的孔附近选取节点，如图11(a)所示。

得到这些节点响应值随频率变化分布，如图12所示。最大响应值出现在上接口右孔的左侧偏下，距离孔中心大约45 mm的节点5102，最小响应值出现在上接口右孔的右侧，距离孔中心大约70 mm的节点7207，如图11(b)所示。

选取参考频率为340 Hz，得到各节点响应值，如表3所示。

2.2.3 位于左边下接口附近节点的响应值计算

在左边下接口施加约束的孔附近选取节点，如图13(a)所示。

得到这些节点的响应值随频率变化分布，如图20所示。最大响应值出现在位于下接口左边2孔的左侧孔下方，距离孔中心大约50 mm的节点5551，最小响应值出现在下接口左边2孔的右侧孔右下方，距离孔中心大约70 mm的节点950，如图13(b)所示。

图11 右激励附近选取节点的位置

图12 右激励附近节点响应值随频率变化分布

图13 左约束附近选取节点的位置

图14 左约束附近节点响应值随频率变化分布

选取参考频率为340 Hz，得到各节点响应值，如表4所示。

2.2.4 位于右边下接口附近节点的响应值计算

在右边下接口施加约束的孔附近选取节点，如图15(a)所示。

得到这些节点的响应随频率变化分布，如图16所示。最大响应值出现在下接口右边2孔的右侧孔右上方，距离孔中心大约15 mm的节点7762，最小响应值出现在下接口右边2孔的左侧孔左下方，距离孔中心大约40 mm的节点7004，如图15(b)所示。

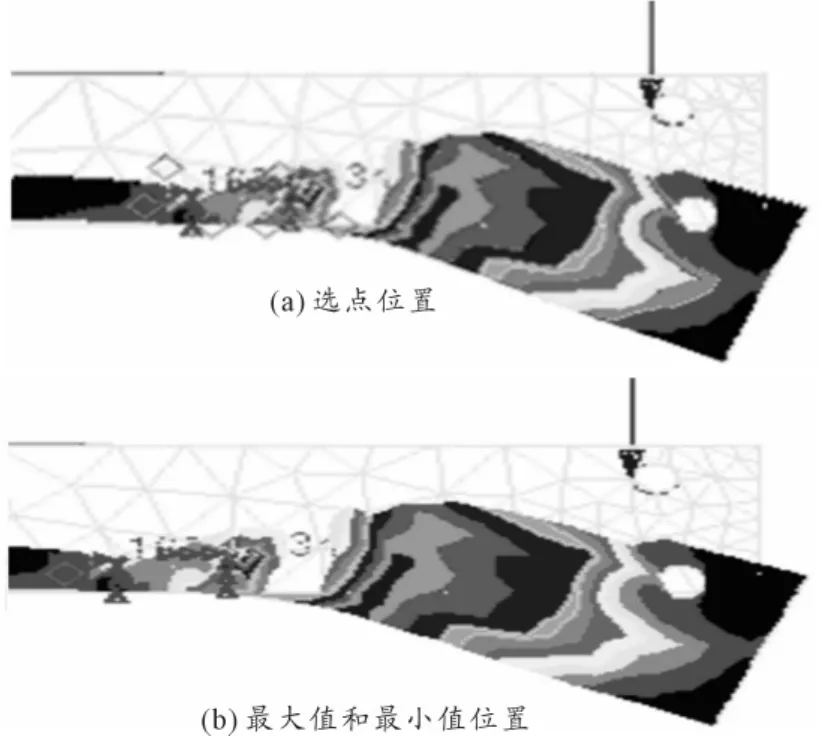
图15 右约束附近选取节点的位置

选取参考频率为340 Hz，得到各节点响应值，如表5所示。

表3 340Hz频率下右激励附近节点的响应值 Pa

表4 340 Hz频率下左约束附近节点的响应值 Pa

表5 340 HZ频率下右约束附近节点的响应值 Pa

图16 右约束附近节点响应值随频率变化分布

2.2.5 控制点的选取

通过以上计算分析，在产品模型施加激励和约束的位置附近的节点响应值都能很清晰地反映出来，为选择振动试验的控制点提供了理论依据。

振动试验本身是一个闭环控制过程，即通过监测控制点的响应来调整所施加的振动激励，以使产品整体响应符合规定要求。因此，控制点的选择便显得尤为重要。分析中，既不希望出现过试验现象，也不希望出现欠试验现象，因而可以利用这种控制机理，根据试验的目的灵活地选择适当的控制点位置。当试验要求产品所有点的响应不超过某一特定值时，选择计算中出现最大响应值的节点作为控制点，便能使得整个产品的各点都不会超过特定响应值;反之，如果要求产品所有响应不底于某一特定值时，则选择计算中出现最小响应值的节点作为控制点，保证整个产品的各点响应值都大于这个特定的响应值;也可测试产品的一个平均水平的响应值分布，这时，只需要把计算出的各节点响应值做一个平均值计算，参照这个平均值寻找几个具有同样响应值的节点作为控制点，便能满足试验要求。

上述方法虽然其结果基本接近目前振动试验中控制点的选择位置，但距离真正意义上的虚拟振动试验尚有一定差距。然而，研究证明，这种使用频率响应分析方法进行振动试验设计的方案是合理可行的。可以预见，随着工作的不断深入，虚拟试验必将成为产品开发阶段的重要手段，将在产品设计开发中发挥巨大作用。