表孔位置对弧门支承结构应力的影响研究
2021-08-27万伟
万 伟
(江西省水投工程咨询集团有限公司,江西 南昌,330000)
0 引言
在拱坝的建设中,表孔通常被用来提升其泄洪能力,而弧门支承结构则是表孔的一个关键部分,这个部位的安全关系着整个拱坝的泄洪能力与安全风险,甚至能够影响整个泄洪枢纽的运行和维护。然而由于其作用原理的特殊性,当表孔位置出现偏移时,其周边地区的弧门支承结构就会更容易受到损坏。通常情况下将表孔设置在轴心区域,但是很多情况下表孔位置都会发生一定的偏移,进而增大弧门支承结构所承受的应力,减少弧门支承结构的使用寿命。南志鹏等[1]详细论述了支承结构应力的计算方式,又添加了静水压力与水底泥沙冲击力对弧门支承结构应力的影响,降低了计算误差。补金梓等[2]研究了表孔位置对堤坝泄洪的重要性,论述了表孔在不同位置下的工作性能。本文结合文献[1]和文献[2]计算不同表孔位置下弧门支承结构所承受的压力,研究表孔位置对弧门支承结构应力的影响。
1 表孔位置弧门支承结构应力计算
1.1 选取弧门支承结构基础参数
假设弧门支承结构的材料均为弹性材质,且拥有性质相似的连续体,因此本文需要在不考虑弧门支承结构对混凝土应力分布影响的前提下,研究表孔对弧门支承结构应力分布的影响,且整个研究过程不涉及孔洞深处、底部以及回廊等部位[3]。在计算该弧门支承结构自重荷载的过程中,需要考虑混凝土的力学性质,且尽量排除弧门自重、表孔埋件以及开关设备荷载的影响,在构建计算模型时也不能考虑修补闸门时添加的二期混凝土所造成的承重荷载影响。关于混凝土基岩的力学性质如表1所示。
根据表1中的混凝土及基岩参数,就可以对整个堤坝的力学性能进行详细的建模计算,在实际计算中通常还需要考虑到弹性模型的动态数值。

表1 混凝土基岩力学性质
1.2 弧门支撑结构应力计算
假定某工程的建造材料为混凝土,坝顶高程约600m,坝底高程约100m,正常情况下堰流水位为500m。当下游水位在平均线以下时,堤坝之前的淤泥高程可以达到550m左右[4]。当堤坝表面的溢流表孔尺寸为10m×15m时,可以得到该堤坝工程的表孔溢流曲线结构图如图1所示。

图1 表孔溢流曲线结构图
想要尽量减少计算过程中的误差,就需要在计算表孔位置对弧门支承结构应力的影响公式之前,将水流荷载考虑在内,包括表孔自重、水纹压力、水底泥沙冲击力、水温温度等,进而计算出弧门支承结构应力。当弧门关闭时,由于水位高程的影响,堤坝上方的水流会给弧门表孔结构施加一个压力,表孔前方的溢流面会通过一定的换算关系对弧门支撑结构产生一定的应力[5]。相应的数值可以通过水库水位的静水压力荷载公式来计算。

式中,P表示水流对弧门支承结构产生的静水压力,MPa;z和 h 之间的关系为-100<z<-h;z表示孔面位置的横坐标,单位为m;h表示孔面位置的纵坐标,即表孔所在的高程,m。而水底的泥沙冲击力则可以通过淤沙重量来计算,其公式如下所示:

式中,F表示水底泥沙的冲击力,N;α表示表孔与弧门承重之间的角度,一般为30°或45°;β表示水底泥沙内摩擦角;z2表示表孔位置的纵坐标,一般情况下取值区间为[-150,-100],m。通过公式(1)和公式(2)可以得到弧门支承结构应力的计算见图2。

图2 弧门支承结构应力计算示意图
如图2所示,弧门支承结构应力的计算公式为:

式中,P1表示弧门上方的水流水平支承结构应力,kN;R表示弧门上方的水流竖直支承结构应力,kN;r表示弧门支撑结构的曲率半径,m;λ表示该河流的水流承重,kN/m3;h表示上游的水流源头距该堤坝的距离,m;v表示表孔的宽度,m;α1和α2分别表示弧门支承结构应力与闸门板面之间角度;P2表示弧门支承结构应力,kN。如此就能够得到表孔溢流过程中拱坝弧门支撑结构应力[6]。
1.3 设定表孔位置
以上文中的公式为核心,构建弧门支承结构的连接体与夹墩模型,并在其中安置表孔结构。整个堤坝模型的坐标严格以原点为中心,呈现出对称结构的形态,其中表孔位置可以有多种选择,不同的位置对弧门支承结构的应力作用有着不同的影响,不过大致处于堤坝主体的中心线附近[7]。尤其是堰流堤坝以及闸门水位的连接部位,表孔位置通常处于堰流顶端,且该表孔位置的局部坐标通常会与堤坝的中心坐标相重叠,并根据水流方向作为判断表孔相对距离的位置。
本文以分析表孔位置对弧门支承结构应力的影响为目的,因此需要分别研究表孔的横向位置与纵向位置对弧门支承结构应力的影响。以堰堤的中心点为原点,构建坐标系,分别设置四个表孔位置距原点的距离为5m、10m、15m、20m,并利用有限元方法计算软件对其进行建模处理,弧门门扇内半径12m、门扉单体重量*门扉数(10t*2)、门扉单体宽度 8m~9.42m,弧门模型见图3,具体的表孔相对堰堤位置示意图见图4~5。
图3 弧门模型

图4 表孔横向相对位置示意图
如图4和图5所示,在探寻表孔位置对弧门支承结构应力影响的过程中,将表孔位置分别设置在横向坐标与纵向坐标中距坐标原点距离5m、10m、15m、20m,由表孔位置的不同得到闸墩内侧面、闸墩外侧面、溢流堰、连接梁等部位的弧门支承结构应力变化规律[8]。
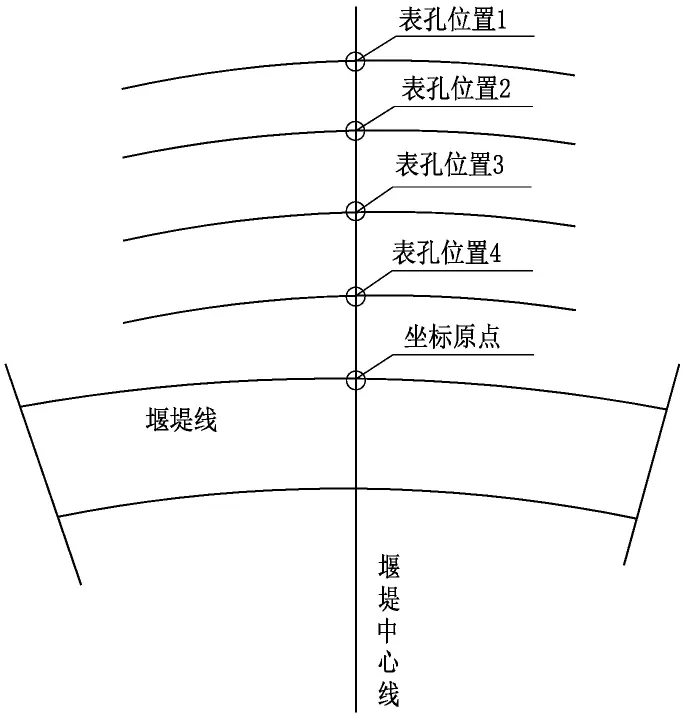
图5 表孔纵向相对位置示意图
2 表孔位置对弧门支承结构应力影响分析
2.1 表孔横向位置对弧门支承结构影响
通过以上计算方案得到表孔横向位置对弧门支承结构中闸墩内侧面、闸墩外侧面、溢流堰交接处、连接梁体四个部位的应力最大值影响数据如表2所示。

表2 不同表孔横向位置下弧门支承结构应力最大值影响数据 MPa
弧门支承结构的应力大致可以分为闸墩正方向的应力与闸墩反方向的应力,表2中闸墩内侧面、闸墩外侧面、溢流堰交接处、连接梁体四个部位所承接的应力会通过一定的反向作用力投射在弧门支承结构中[9]。由此可以得到四个横向表孔位置对弧门支承结构正向应力与反向应力产生的影响如图6~7所示。

图6 不同表孔横向位置下闸墩正向方位应力
如图6所示,当坐标原点与表孔位置之间的距离小于10m时,弧门支承结构应力提升幅度较小,只从初始的2.65MPa增长为10m距离的3.05MPa,但是当坐标原点与表孔位置之间的距离大于10m时,该数据的最大值就开始呈现出急剧的上升趋势,距离为20m时,应力的最大值可以达到6MPa,而最小值虽然也是上升的状态,但是其提升幅度较小,只从5m的0.85 MPa提升到了20m的1.55 MPa[10]。这样的弧门支承结构应力变化趋势为:当表孔位置距离坐标原点越来越远时,弧门支承结构所承受的正向方位应力也会随之增大,但是其应力的最大值和最小值波动幅度也在相应变大。
如图7所示,在反向方位的不同表孔位置下,弧门支承结构应力的最大值也在随着表孔位置与坐标原点位置的增大而增加,只是其增长幅度比较均匀,且斜率较小,坡度较缓。弧门支承结构应力的最小值则是一个先减小后增加的变化趋势,在距坐标原点5m时为2 MPa,当表孔位置距坐标原点为10m时应力降低至1.6 MPa,当表孔位置继续增大时其弧门支承结构应力的最小值又继续增大,直至20m时为2.4 MPa。这样的变化是因为在闸墩反向方位中,由于表孔位置短距离偏移产生的一个水流回旋力,致使其所受到的应力短暂减小,但是在偏移幅度越来越大后,这个反作用力也会逐渐消失,使应力变化重新回到上升的趋势[11]。

图7 不同表孔横向位置下闸墩反向方位应力
2.2 表孔竖直位置对弧门支承结构影响
通过以上计算方案得到表孔纵向位置对弧门支承结构中闸墩内侧面、闸墩外侧面、溢流堰、连接梁四个部位的应力最大值影响数据见表3。

表3 不同表孔纵向位置下弧门支承结构应力最大值影响数据 MPa
如表3所示,随着表孔位置与坐标原点距离的增加,闸墩内侧面、闸墩外侧面、溢流堰交接处、连接梁体四个部位应力均值也在不同程度地减小。将这四个部位的反作用力投射到闸墩正向与反向的作用力中,可以得到如图8~9所示的不同表孔纵向位置下闸墩正反方向应力。

图8 不同表孔纵向位置下闸墩正向方位应力
如图8所示,纵向排列的四个表孔位置在正向方位下受到的弧门支承结构应力呈现出逐渐增加的趋势。其最大值从5m的2.7MPa逐渐提升至20m的5.9 MPa。在最初的10m内,应力增长速度较为缓慢,但是当表孔的纵向位置距坐标原点超过10m时,弧门支承结构应力增长速度就会大幅度提升[12]。弧门支承结构应力的最小值增长速度相较于最大值略慢,当表孔距坐标原点为5m时,弧门支承结构应力为1.05 MPa,之后的应力增长速度十分均衡,至20m时达到了2MPa。根据图8可知:当表孔位置在纵向轨迹上远离坐标原点时,若表孔位置与坐标原点相距不超过10m,则对弧门支承结构应力不会有太大的影响;但是当表孔位置与坐标原点相距大于10m,弧门支承结构应力就会变大,两者之间距离越远,该数值的增长速度就会越快,且最大值和最小值之间的差距也会逐渐扩大,使应力作用在水流的影响下逐渐失衡。
如图9所示,对于弧门支承结构的反向方位应力,随着表孔位置与坐标原点距离的增大,呈现出一定的变化。弧门支承结构应力最大值一直呈现出不断增长的趋势,从5m距离的2.95MPa以一次函数的轨迹增长至20m距离的4.15MPa。而弧门支承结构应力最小值的变化轨迹则较为复杂,在二者相距5m时,弧门支承结构的反向方位应力最小值为1.9MPa,随后的应力曲线有较小幅度的下降,直至二者相距10m时才逐渐开始小幅度提升,到二者相距20m时弧门支承结构的反向方位应力约为1.95MPa。
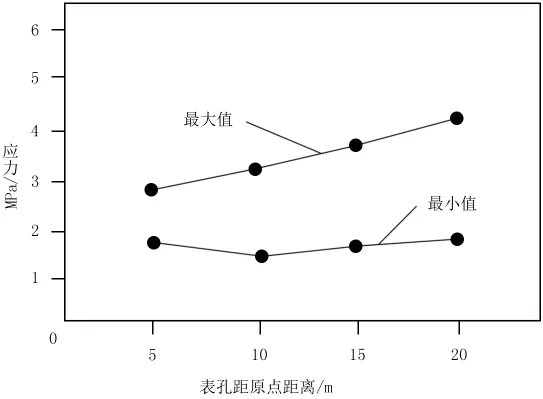
图9 不同表孔纵向位置下闸墩反向方位应力
3 结论与展望
本文系统地计算了不同表孔位置下弧门支承结构所应承受的压力,重点在于横向或纵向表孔位置不同的前提下弧门支承结构的受力性能变化,并得到了一定的成果,初步展示了表孔位置对弧门支承结构应力的影响。所得研究结论分别为:
(1)在正向方位的弧门支承结构应力变化中,随着表孔位置与坐标原点距离的增加,弧门支承结构应力的最大值与最小值之间的差距也会相应增加,当二者距离小于10m时,表孔位置对弧门支承结构应力的影响不大;只有当二者之间距离超过10m,弧门支承结构应力才会随着距离的增加而增大。
(2)在反向方位的弧门支承结构应力变化中,随着表孔位置与坐标原点距离的增加,弧门支承结构应力的最大值与最小值之间的数值不会有较大差距,其最大值一般会以小而均衡的增长幅度持续增长,而最小值则会呈现出反复变化的趋势。
虽然本次研究分析了表孔位置对弧门支承结构应力的影响,但是在整个计算过程中,有关河流对弧门支承结构的作用力涉及较少,此处的计算过程中会有一定的误差,因此在之后的研究中,可以进一步计算,并对表孔位置的影响效应做出新的判断。


