拓扑绝缘体界面的透射极化旋转*
2019-10-09陈芳芳
陈芳芳
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
0 引 言
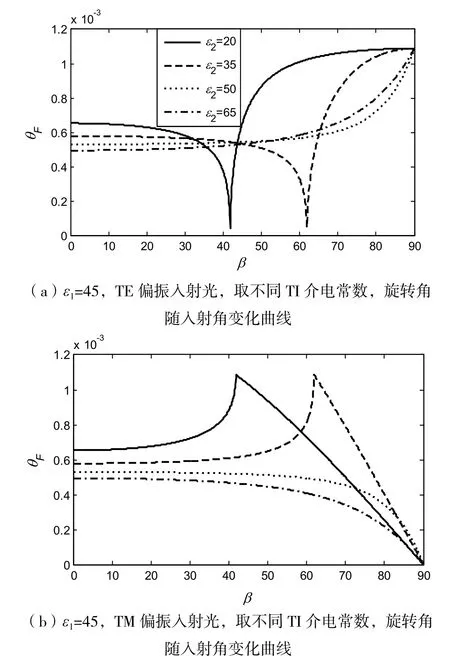
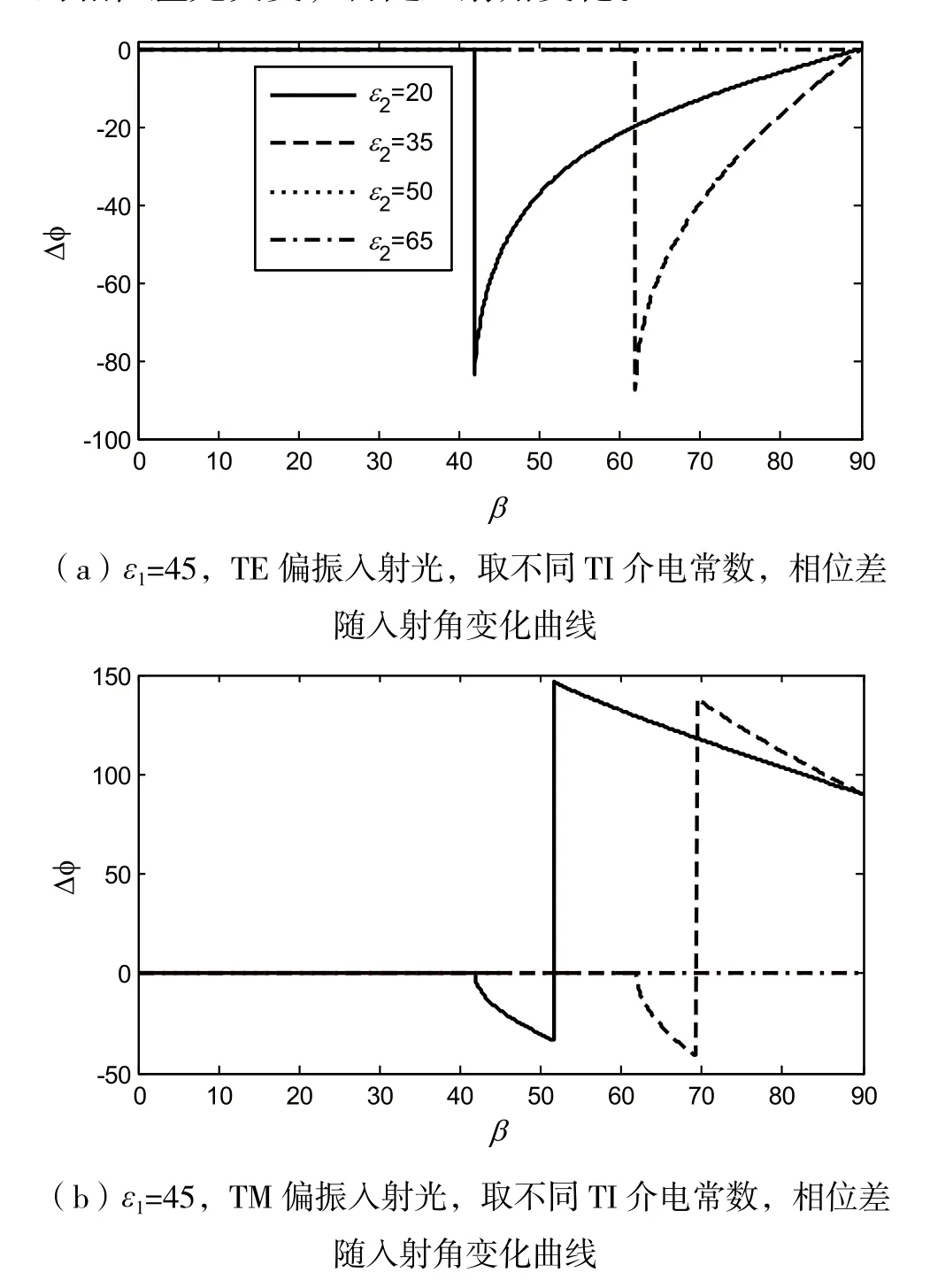
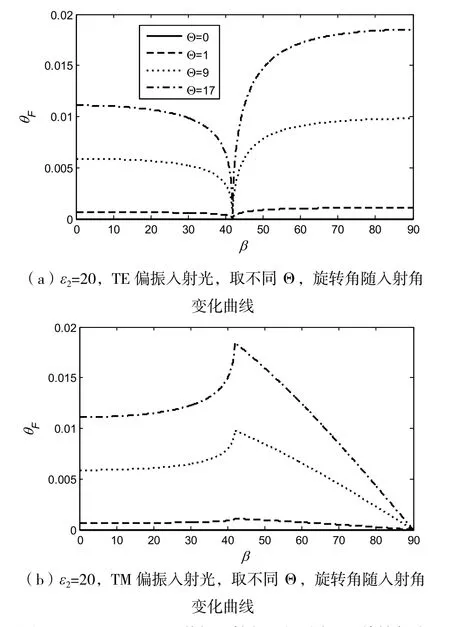
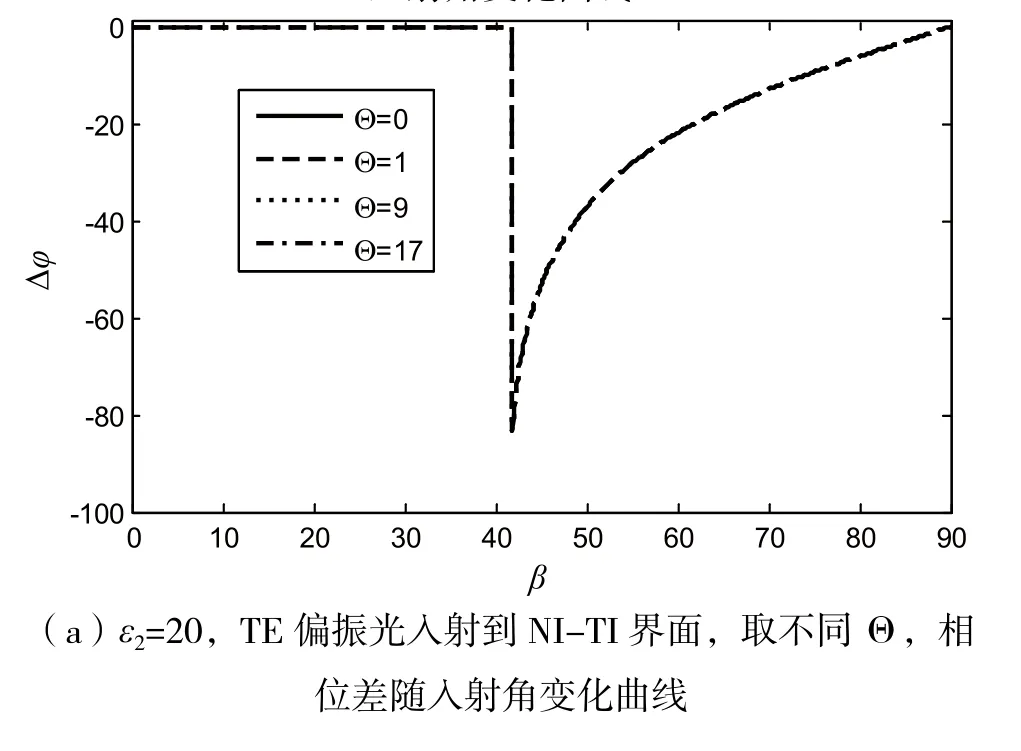
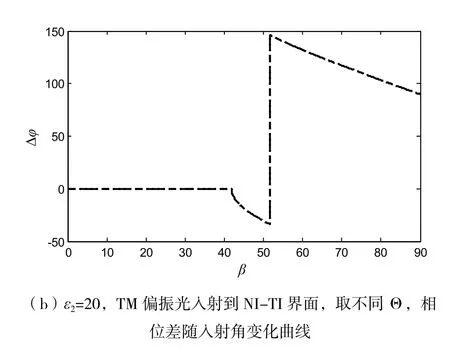
拓扑绝缘体(Topological Insulator,TI)能用自旋螺旋结构和狄拉克能量色散模型描述,是一种具有强自旋-轨道耦合效应并受时间反演对称保护的全新物质[1-2]。对TI的研究最早能追溯到1879年发现的霍尔效应[3],人们在80年代以前用Landau的对称性自发破缺理论作为物质状态分类依据,但是之后发现的量子霍尔态无法用有效场论进行解释,从而诞生了量子场论以及能带理论。TI有量子螺旋边界态和绝缘体态,其奇特性质可以能用拓扑场论用有效拉格朗日项:L=1/8π(εE2-1/μB2)+αΘ/4π2(E·B)描 述[4]。 按 照 维 数 TI能 分为三类:(1)聚乙炔(一维);(2)石墨烯和CdTe/HgTe等(二维);(3)Bi1-xSex(0.07 极化转换器[7-10]是一种不改变入射偏振态,改变入射偏振面方向的器件,能应用于天线、液晶显示等设备。近几年,由于可以旋转入射光的偏振面,各向异性介质、扭曲向列液晶以及手征特异材料等特殊材料都受到了广泛的研究[7]。在TI外加电场会在同方向上诱导出磁场,外加磁场同样会引起电荷极化,即TI有拓扑磁电效应(Topological Magnetoelectric Effect,TME)[11-12]。 由 于 存 在TME,频率为约化普朗克常数)的线偏振光垂直入射时,文献[1]中计算得ε´,μ´到铁磁体和TI分界面处的存在Faraday偏转角其中ε,μ和分别表示铁磁体和TI的介电常数和磁导率,α为精细结构常数,Δ为拓扑磁电极化项。刘等[13]研究了TI界面的反射极化偏转性质,本文计算了普通绝缘体和TI分界面处的透射极化旋转角和相位差,并分析了材料参数和拓扑磁电极化率对透射性质的作用。 时谐场为e-iωt的线偏振光,从拓扑磁电极化率为0的半无限普通绝缘体(Normal insulator,NI)(介电常数和磁导率分别为ε1,μ1)沿z轴正方向斜入射到拓扑磁电极化率为Θ的半无限TI(介电常数和磁导率分别为ε2,μ2),如图1所示。由于存在TME,和普通本构方程不同,TI修改后的本构方程为: 外加平行于z轴负方向的磁场(B)后,打开了TI表面的能隙,透射光偏振面发生旋转。入射和透射的电场分量用琼斯矢量法[14]分别表示为: 透射极化旋转角θF是透射光的偏振面旋转角度,与入射光的偏振态有关。垂直(Transverse Electric,TE)偏振光入射,即b=0时,透射旋转角为: 平行(Transverse Magnetic,TM)偏振光入射,即a=0时,透射旋转角为: 透射光的平行和垂直电场分量可以用幅度和相 位 表 示 为:u=|u|eiφu=tTE,TEa+tTE,TMb和v=|v|eiφv=tTM,TEa+tTM,TMb,其中相位差为 Δφ=φu-φv。TE 偏振光入射,即b=0时,相位差为: TM偏振光入射,即a=0时,相位差为: 单界面TI的透射系数和入射角、拓扑磁电极化率以及材料参数都有关,本文研究的NI和TI都是非磁性材料,μ1=μ2=1。首先取ε1=45,Θ=π,TI的介电常数取不同值:20,35,50,65。观察图2可以发现,θF≠0,即TI表面存在极化旋转。 图2 ε1=45,TE和TM偏振入射光,取不同TI介电常数,旋转角随入射角变化曲线 当入射角β=0,即垂直入射时,TE和TM偏振入射的透射θF都相等;当入射角β=90°,即掠入射时,TE和TM偏振光的透射θF分别取最值。当ε1>ε2时,存在临界角θc=arcsinn2/n1。介电常数越大,β<θc,θF的值越小,θF的谷值或峰值右移,但是θF的最大值不变。当ε1<ε2时,TE(TM)偏振光的透射θF随入射角单调递增(递减),其中介电常数越大,TE偏振光的θF变化速度越快;TM偏振光的θF值越小。 如图3所示,不能发生全反射时,透射系数都为实数,即透射光的相位差为0。能发生全反射时,由于非对角透射系数不为0且变为复数,因此相位差会变成随入射角变化的曲线。只有tTE,TM不随入射角变化为常数,TE和TM偏振光的相位差随入射角变化规律不同。不能发生全发射时,透射光的相位差为0,即偏振态不变;发生全反射时,透射光的相位差先突变,再随入射角变化。 图3 ε1=45,TE和TM偏振入射光,取不同TI介电常数,相位差随入射角变化曲线 取材料参数:ε2=20,其他参数和图2的相同,改变拓扑磁电极化率(只能取奇数倍的π),θF曲线如图4所示。当Θ=0时,两种情况的θF都为0,即极化旋转是由TI引起的。改变Θ,两种情况的θF能够得到明显的增强,且曲线形状和图2中相同,不发生改变。改变Θ,相位差随入射角变化规律和图3中ε2=10曲线的规律相同,不受的Θ影响(见图5)。 图4 ε2=20,TE和TM偏振入射光,取不同Θ,旋转角随入射角变化曲线 图5 ε2=20,TE和TM偏振光入射到NI-TI界面,取不同Θ,相位差随入射角变化曲线 本文根据单界面TI的透射系数矩阵,研究了材料参数和拓扑磁电极化率对透射θF和相位差随入射角变化曲线。TI的透射光存在极化旋转且相位差能发生改变,有希望应用于极化偏转器和偏振态调控。研究结果表明能够通过增大拓扑磁电极化率,在不改变偏振态的情况下增大透射极化旋转,但是θF的值仍较小,实际应用还需要进一步研究。1 单界面拓扑绝缘体


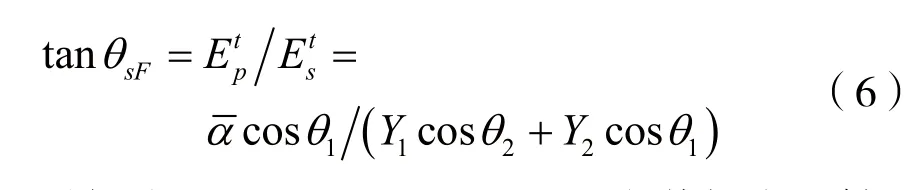
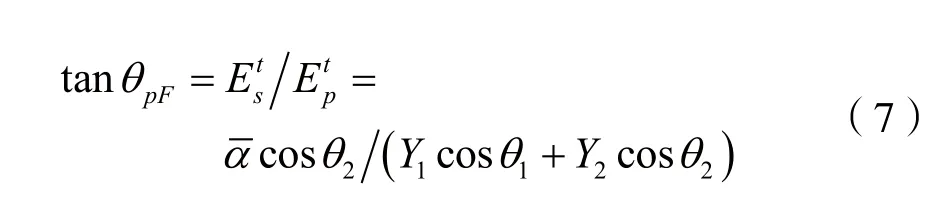


2 数值仿真
3 结 语
