OFDM系统中低失真峰均比抑制模块设计实现*

郭强胜，郑 重，肖 飞，杨建平

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

正交频分复用[1]（Orthogonal Frequency Division Multiplexing，OFDM）技术是适用于在无线信道环境下的高速数据传输技术，其具有高传输速率、强抗干扰能力等优点，既可用于民用移动通信，也可应用于军事高速专网通信。但是，OFDM系统在设计原理上就注定存在其固有的缺陷，即多个子载波的相互叠加会产生峰均比较高的时域信号。在这种情况下，系统的功率放大器就需要有较大的线性区间，使该功放的线性工作范围大于OFDM系统峰值功率和平均功率的占据区间，从而满足OFDM系统中信号的无失真传输[2]，但这种做法会导致功率放大器的效率会大大降低，其中绝大部分能量成为热能浪费掉。另外扩大功率放大器的线性区间也将引起设备成本的增加，在移动通信设备中都是绝对不允许的。因此，必须找到有效的方法来降低OFDM系统的峰均比。峰值脉冲抵消削峰（Pulse Cancellation Crest Factor Reduction，PC-CFR）是限幅削峰法[3]中的一种，该算法首先找出待削峰值，然后与系统的削峰脉冲相减，最终达到削峰的目的。其中削峰脉冲是频率响应与待削峰时域信号具有相同带宽的滤波器的冲击响应，该削峰方法可最大限度的保持被削峰值信号的相位不发生偏转。该算法不会降低系统的误比特率（BER），且数据子载波数据不会产生失真，是一种较好的降低峰均比的方法。

1 峰值脉冲抵消算法原理

在大部分系统中，基于波峰因子的削峰算法都是将待削峰值信号与削峰修正信号相减，其实现原理如图1所示。

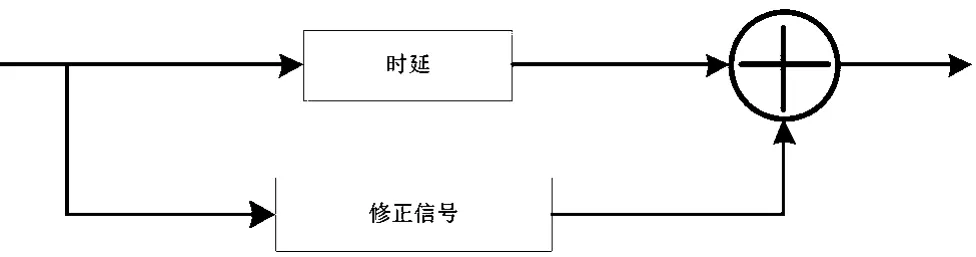
图1 CFR算法基本原理

算法中修正信号的频率响应与待削峰峰值信号在频率响应上是相同的。在PC-CFR算法[4]中，修正信号是一些相互独立的对消脉冲的和集。其中，每一个独立的对消脉冲是与被削峰信号频谱相同的滤波器的冲击响应产生而成。

图2表明了峰值对消CFR算法的峰值检测过程，寻找到系统超过设定阈值的峰值后，计算出幅度超过设定门限值的部分(A-Ath)。

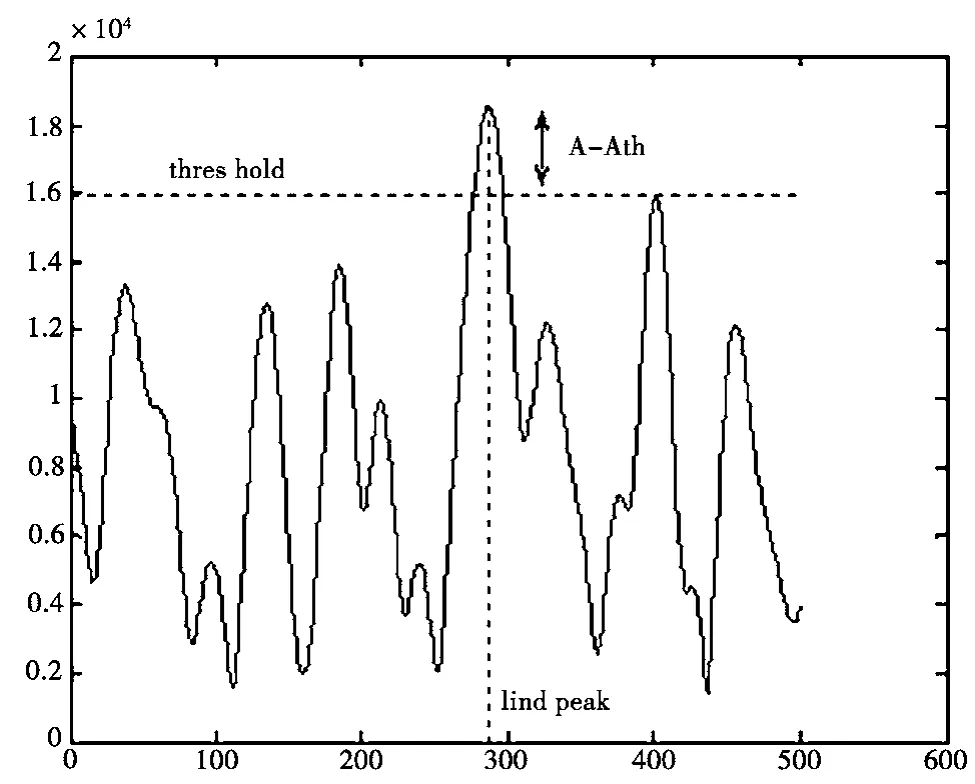
图2 峰值检测过程

图3表示的是该削峰算法中使用的抵消脉冲，该脉冲是由单位幅度信号的冲击响应与(A-Ath)×eθ相乘而生成，θ是信号峰值相位。由此看出，抵消脉冲是由信号峰值减去削峰门限部分的信号幅度与信号相位共同产生而成[5]。实际系统中每个发送信号都是复信号，抵消脉冲须具备与相应峰值信号相一致的相位。

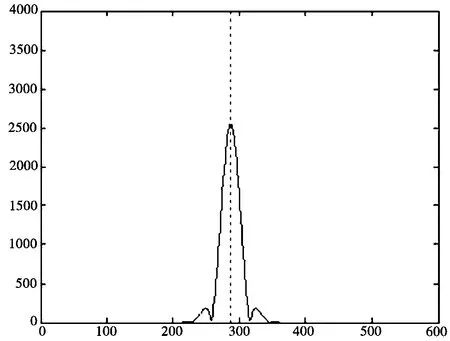
图3 削峰脉冲

如图4所示，用原始峰值信号减去相对应的抵消脉冲，可将峰值信号的幅度降低到门限值以下，同时保持了信号的相位不变，具有较低的失真度。

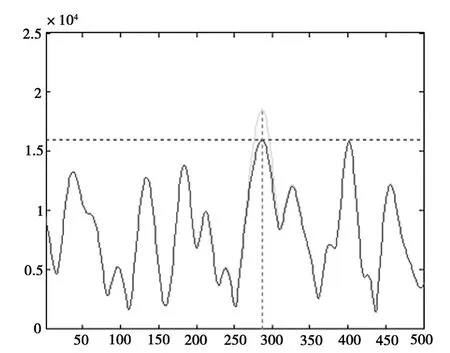
图4 峰值抵消

在硬件实现中，抵消脉冲是通过抵消脉冲生成器（Cancellation Pulse Generator，CPG）产生的，如图5所示。当检测到信号峰值到来时，控制地址计数器产生单位削峰脉冲，同时将此峰值信号与削峰门限的幅度差值和相位输入到复数乘法器，从而产生与该峰值相匹配的削峰脉冲[4]。

一般情况下，削峰算法经过一次削峰后并不能把系统所有的超过门限值的峰值都削除到阈值以下，此时需要算法进行多次迭代削峰来消除系统所有的峰值信号[6]。算法的复杂程度和资源占用情况取决于需要进行的迭代削峰次数。

一个典型峰值脉冲抵消算法的详细实现结构如图6所示。

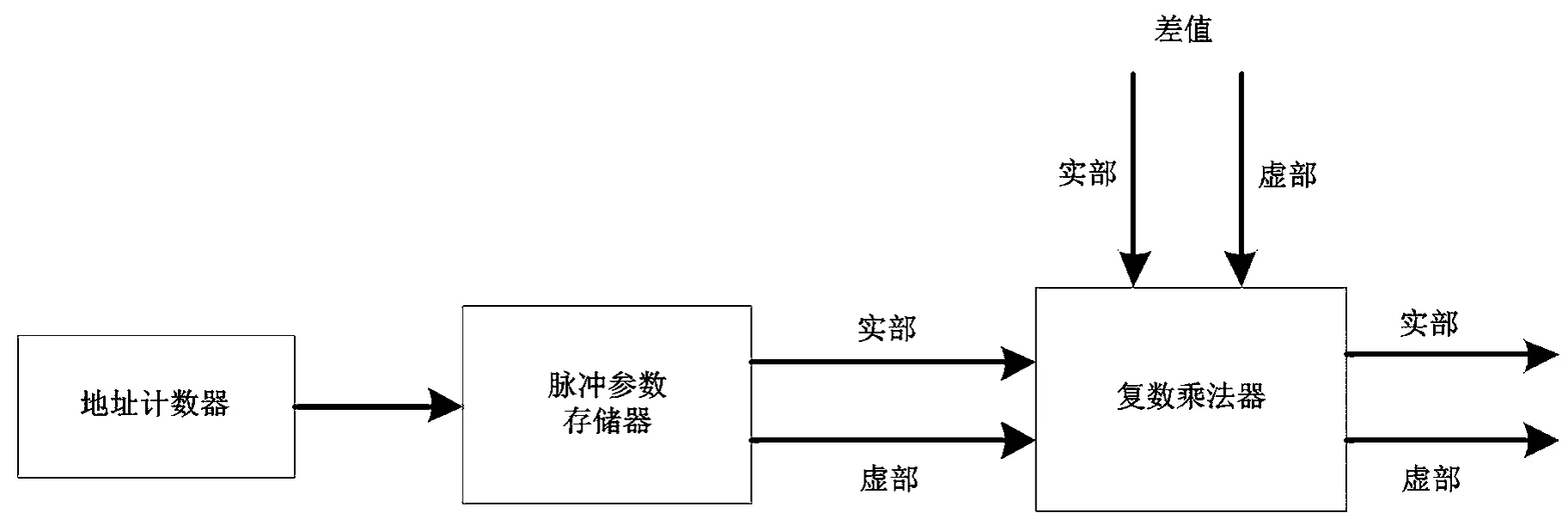
图5 抵消脉冲生成器

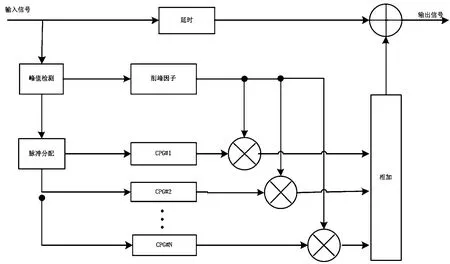
图6 峰值脉冲抵消算法原理框图

（1）峰值检测

峰值检测模块完成在一个设定区间内查找出超出设定阈值幅度的信号峰值，这些设定区间和设定阈值都保存在特定寄存器中。

在PC-CFR算法中，有两种峰值检测的方法。第一种方法是比较当前数据点与前一时刻数据点的幅度值，如果当前数据点幅度大于前一时刻数据点的幅度值，并且大于系统设定的削峰门限值，那么就可判断当前数据点就是检测到的信号峰值；第二种方法是，在一个特定的门限区间内寻找信号幅度的最大值作为检测到的信号峰值。假如一个特定的门限区间为[x1，x2]，此时的信号幅度曲线与系统设定的削峰门限值相交于x1和x2两个点，同时x1和x2之间的信号幅度均大于系统设定的削峰门限值。

第一种峰值检测方法具有实现简单、检测延时较固定的优点；但是当系统时域信号峰值点出现很密集时，算法对该密集信号峰值点进行削峰处理时的噪声可能会相互叠加增强，出现信号峰值再生的不好现象。第二种峰值检测方法，由于其在一个特定的门限区间内只会检测到一个峰值，在削峰处理时只有该点会引入削峰噪声，没有出现噪声叠加从而形成峰值再生的可能性，但该检测方法在工程实现中较第一种复杂。

图7为两种峰值检测过程的示意图[6]。采用第一种峰值检测方法，可以在两个限幅区间检测到A、B和C共3个峰值；采用第二种峰值检测方法，可以在两个限幅区间检测到A和C共2个峰值，此时B不能成为峰值。

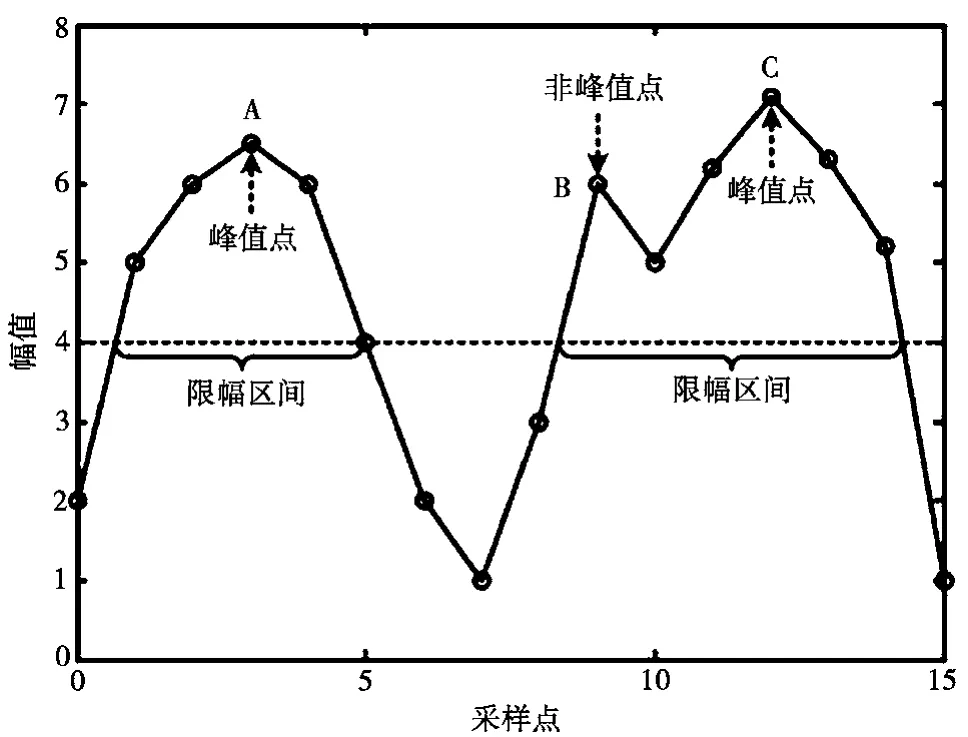
图7 第二种峰值点的定义

（2）削峰因子

削峰因子模块主要是为算法抵消脉冲生成幅度和相位的复数调整因子。该复数因子用来修正削峰脉冲的幅度和相位，保证经过削峰后的信号与原始信号具有相同的相位。为了满足上述要求，将检测到的峰值信号的削峰因子作用于与该峰值相对应的削峰脉冲系数。该模块将峰值检测模块检测到的超过设定门限值的峰值信号的幅度和相位作为输入，信号峰值与门限值的差值就是削峰因子的幅度，信号峰值的相位就是削峰因子的相位。可用下式的数学式表示。

式中，θ是峰值信号的相位，|x|是信号峰值的幅度，γ是削峰门限值，a就是峰值因子。

（3）抵消脉冲发生器

抵消脉冲发生器是整个削峰算法的核心，主要用来产生与峰值信号相匹配的削峰处理抵消脉冲。抵消脉冲实质是滤波器，可通过在MATLAB软件内的滤波器设计方法得到，其设计频带宽度与峰值信号相同。算法将已设计好的滤波器系数预先放置在存储器中。

在设计抵消脉冲滤波器[5]时，需要在滤波器系数长度和性能之间达到平衡。如果滤波器的过渡带设计得很陡峭，此时滤波器的系数长度就较长，这样设计的后果就会导致算法的削峰密度降低，容易遗漏峰值。如果滤波器的过渡带设计过长，将会造成严重带外泄露。因此，在设计滤波器的时候，考虑邻道泄露比[7]（Adjacent Channel Leak-age Ratio，ACLR）在满足系统要求的前提下，采用尽可能短的滤波器系数。

（4）脉冲分配器

算法在进行削峰处理时，脉冲分配器主要负责CPG的分配使用。在初始状态，所有的CPG都处于空闲态。当算法检测到第1个峰值信号到来时，脉冲分配器为该峰值分配一个空闲的CPG用于削峰处理，同时算法把该CPG由空闲态标记为占用态，直到此峰值的削峰过程结束后才释放；算法继续检测其他峰值信号到来，并为其分配剩下的空闲CPG，直到所有空闲的CPG分配出去。

如果检测到超门限值的信号峰值过于密集，可能出现可分配的CPG的数量不能满足峰值需求。针对此种情况，在实际的系统中通常需要设置CPG分配间距参数，只有大于该参数间距的峰值才会被分配CPG。小于该参数间距的峰值将不会被分配CPG，当前的峰值不会被处理。

2 算法实现

2.1 顶层设计

峰值脉冲抵消算法可根据实际系统削峰门限值设置的高低来决定采用几次迭代削峰，经过多次迭代后基本都可达到预期的抑制效果。该算法采用两次迭代实现，为达到更好的抑制效果，可以根据实际需要增加迭代次数，其中每个迭代模块是相同模块的重复调用。其顶层设计如图8所示。

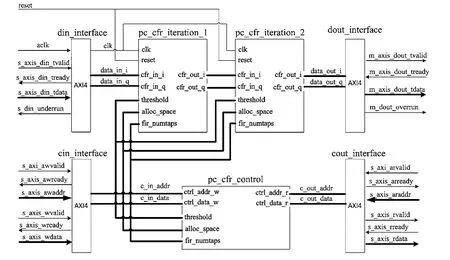
图8 算法实现顶层设计

2.2 模块实现

峰值脉冲抵消算法的实现是参照算法的原理框图来逐一实现的。算法首先将数据进行cordic坐标转换，计算出当前数据的幅值和相位；然后使用峰值检测模块来检测时域数据流超过设定门限值的峰值，同时根据检测到的峰值数据计算出削峰因子（幅度差值和相位）；利用削峰因子参数实时产生与待削峰值相匹配的抵消脉冲；最后将该峰值信号经过适当的延时后与相匹配的削峰脉冲相减得到削峰后的数据。

（1）cordic模块：主要完成信号的幅值和相位的计算。信号的幅值主要用来峰值检测，信号的相位主要为生成削峰脉冲提供相位参数。

（2）峰值检测模块：该模块采用上述提到的第二种检测方法，在超过门限阈值的多个信号中，最大的那个峰值初判定为该区间的峰值，此时要等到信号幅值下降到门限阈值下面才能真正的确定区间峰值是真正的峰值。

该模块主要由比较器实现，实时的比较超过设定门限值和信号的幅值。该模块把内部控制信号为new_peak和search_start信号。在初始状态，new_peak为低电平，search_start为高电平。当检测到信号的幅值大于设定门限值，search_start信号变为低电平，标志开始峰值检测过程；在检测过程中，如果新的信号的幅值大于当前记录的信号幅值的最大值，new_peak信号变为高电平，并将新的信号的幅值更新为记录的信号幅值的最大值，如果新的信号的幅值低于当前记录的信号幅值的最大值，new_peak信号变为低电平；如果新的信号的幅值重新低于设定门限值，search_start信号变为高电平，标志一次峰值检测过程结束。

（3）削峰因子模块：该模块将检测到的峰值信号与系统设定的门限值相减，计算出二者的差值，同时根据检测到的峰值信号的相位计算出二者差值的相位，得到削峰因子的虚部和实部参数。

（4）抵消脉冲生成器模块：该模块是整个设计实现的核心模块。如图9所示，整个模块包括复数乘法器（Complex MAC）、乘前延时器（pre_mac_delay）、CPG系数存储器（filter_ram）、CPG复用器（CPG Multiplexing）和CPG分配器（CPG_allocator）组成。

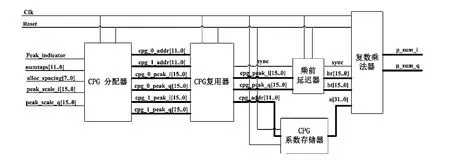
图9 抵消脉冲生成器

该模块采用分时复用的工作方式。削峰脉冲的冲击响应滤波器参数预先存放在系数寄存器中。当峰值信号到来时，CPG分配器根据削峰脉冲发生器的使用情况来为其分配削峰脉冲。CPG复用器模块完成CPG地址值和削峰因子的时分多路切换，其中CPG地址用于读出保存在ROM中的滤波器系数，削峰因子作用于复数乘法器。复数乘法器模块利用削峰因子对完成对滤波器系数的缩放和相位处理。乘前延时器模块将进入复数乘法器的数据进行延时处理来对齐待削峰数据。最后将对齐后的数据相减，完成一次削峰处理。

3 仿真及结果分析

3.1 MATLAB仿真

利用MATLAB软件对模块进行仿真，仿真环境为OFDM多载波系统，信道带宽20 MHz，子载波数为1 200个。在正常情况下，峰均比抑制门限值设置的越低，采用相同迭代次数的算法对峰均比抑制的效果越差，同时对系统性能造成的恶化更大。

（1）抑制门限值为5 dB

当峰均比抑制门限值设置为5 dB时，算法采用两次迭代后的抑制效果如图10所示。

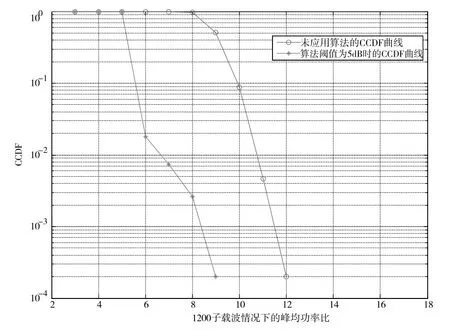
图10 门限值为5 dB的峰均比抑制效果

对信噪比的恶化影响如图11所示。从仿真的结果看，该抑制算法可将大部分输入信号的峰值抑制到5 dB以下，但是仍有少部分信号只被抑制到9 dB，并且此种情况下的信噪比损失[8]约在1 dB左右。

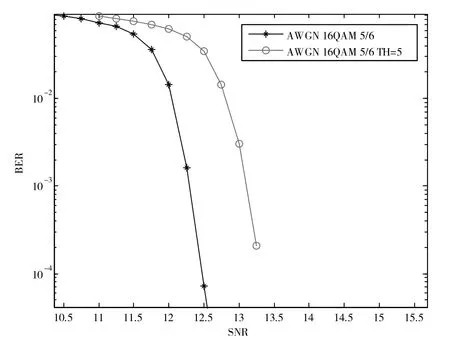
图11 峰均比抑制模块对信噪比的影响（TH=5）

（2）抑制门限值为7 dB

当峰均比抑制门限值设置为7 dB时，算法采用两次迭代后的抑制效果如图12所示。

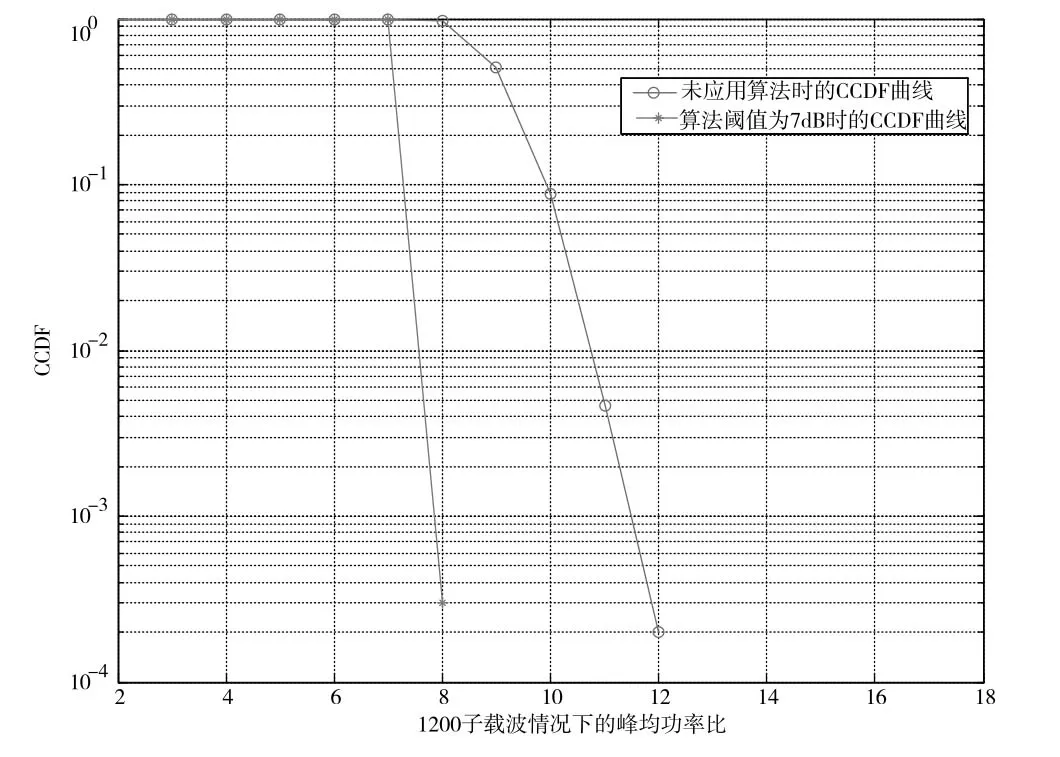
图12 门限值7 dB的峰均比抑制效果

对信噪比的恶化影响如图13所示。从仿真的结果看，该抑制算法可将绝大部分输入信号的峰值抑制到7 dB以下，只有极少部分信号可到达到8 dB，并且此时的信噪比损失小于0.1 dB。

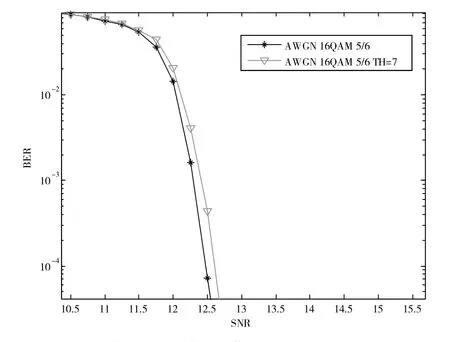
图13 峰均比抑制模块对信噪比的影响（TH=7）

从上述仿真结果来看，该削峰算法能够对OFDM多载波系统进行峰均比抑制。当峰均比抑制门限设置为5～6 dB时，该抑制算法通过两次迭代削峰后仍有部分峰值信号没有被有效抑制掉，同时对系统的信噪比有较大的恶化；当抑制门限设为7 dB时，该算法只有极少数的峰值信号没有被抑制掉，此种情况下信噪比几乎无恶化。总体来看，对具有1 200个子载波的OFDM系统，将峰均比抑制到7 dB是完全可行的。

3.2 Modelsim仿真

将采用两次迭代的抑制算法在FPGA内进行了设计实现，同时用ModelSim软件进行了仿真验证。在MATLAB和ModelSim仿真时采用相同的数据流作为算法的激励，比较MATLAB和ModelSim的输出数据流，以此来判断FPGA算法实现的正确性。在进行FPGA模块的仿真验证时，同样将抑制门限值设置为5 dB和7 dB。

（1）抑制门限值为5 dB

门限为5 dB时的MATLAB仿真结果如图14和图15所示。其中图14（a）是该抑制算法经过第1次迭代后的时域数据仿真图，图14（b）是该抑制算法经过第2次迭代后的时域数据仿真图。从图中可以看出，输入数据在经过抑制算法第1次迭代后仍有大量的峰值信号未被抵消掉；在经过第2次迭代抑制后，超过门限阈值的峰值虽有减少，但仍然很多。这就意味着门限值设置为5 dB，算法采用2次迭代是不能完全将峰值信号抑制在门限值以下的。图15是MATLAB仿真输出的部分数据值。

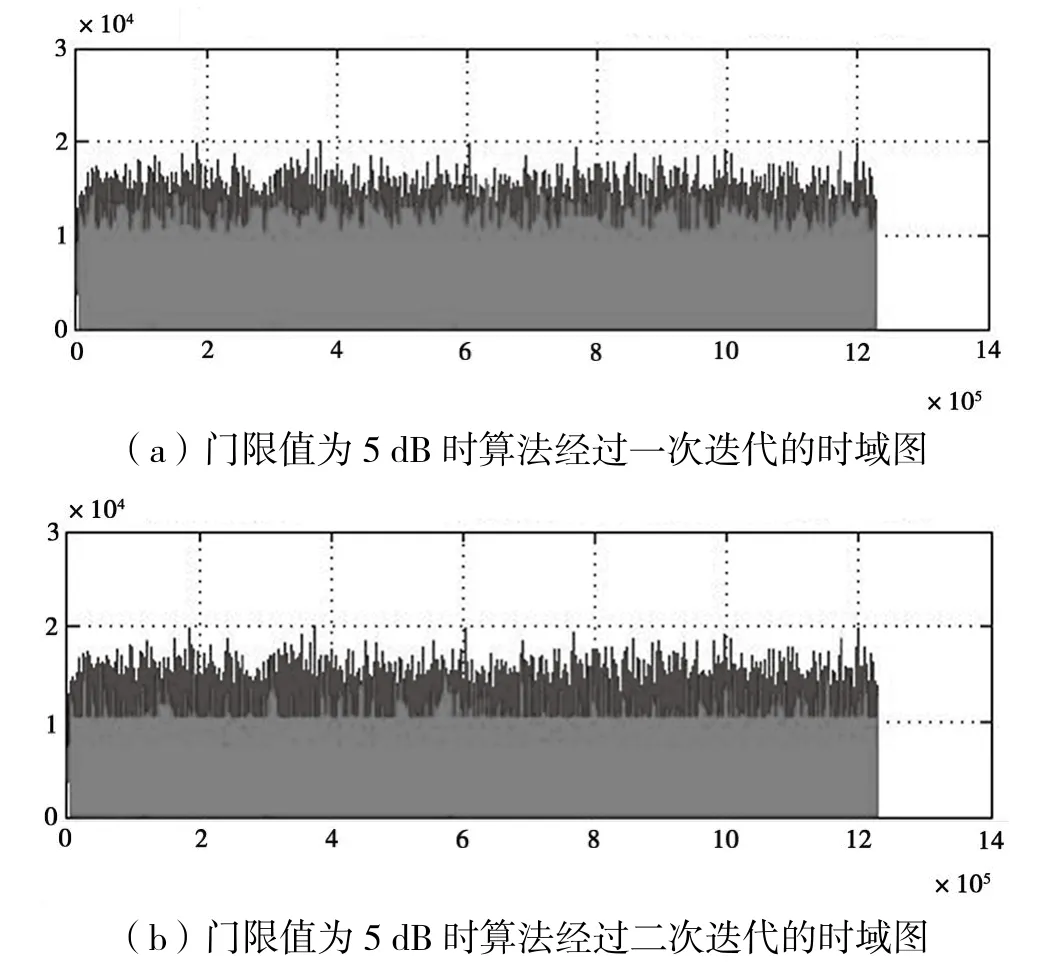
图14 门限值为5 dB时MATLAB时域仿真图

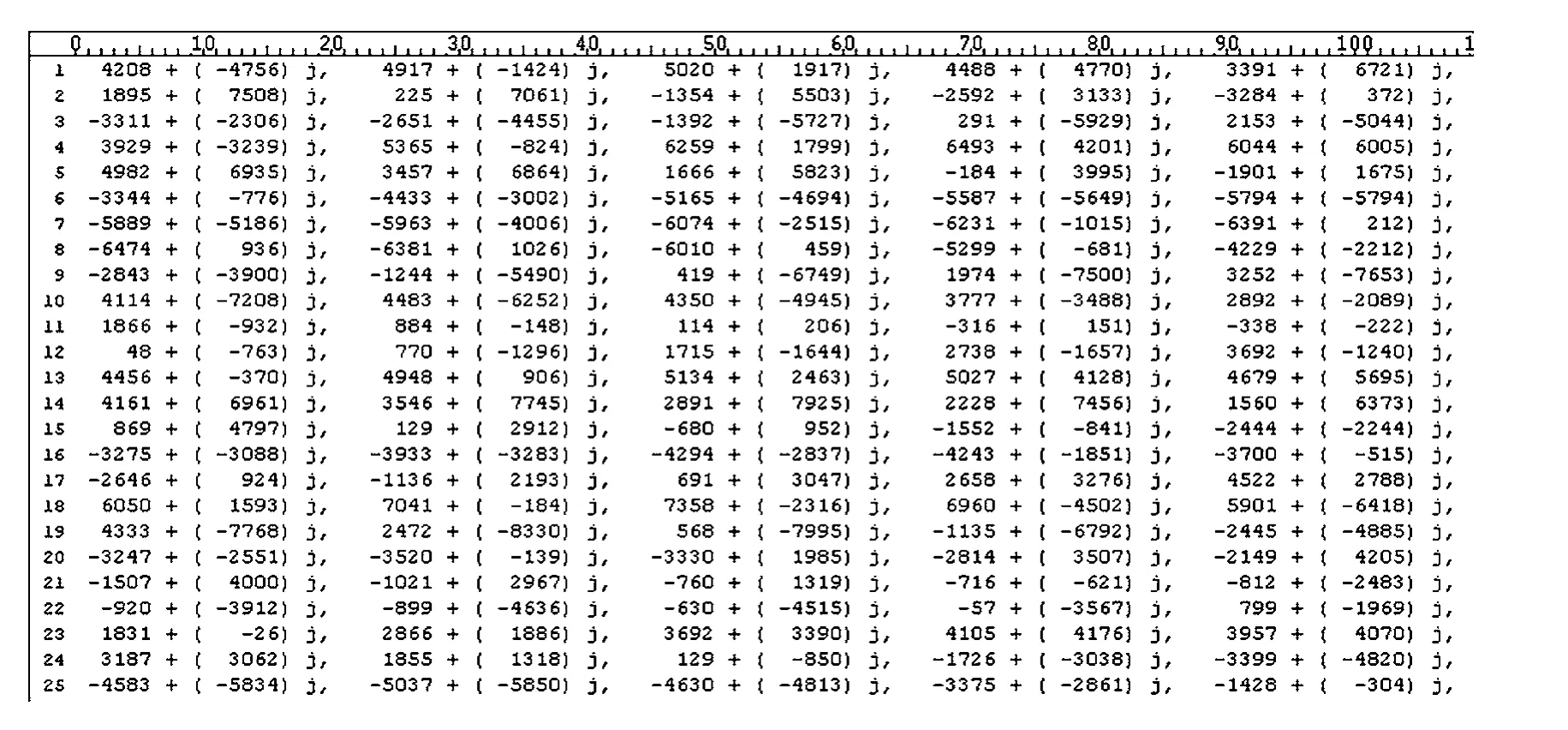
图15 门限值为5 dB时MATLAB仿真输出数据

该算法的FPGA实现模块采用ModelSim软件仿真的结果如图16、图17所示。在图16中，上面的时域数据图是算法在第1次迭代后的输出数据流，下面的时域数据图算法在在第2次迭代的输出数据流。可明显的看出，算法在第2次迭代削峰抑制后超过设定门限值的峰值比第1次迭代后的峰值要减少很多，但仍然有少部分峰值超过设定的门限值，该ModelSim仿真结果与Matlab仿真结果是一致的。

FPGA算法模块经过ModelSim仿真后的部分数据如图17所示，通过对比图15和图17中的数据值，发现两者完全相同，这样就可以证明算法在FPGA中的实现与MATLAB仿真达到了相同的效能，验证了FPGA实现的正确性。

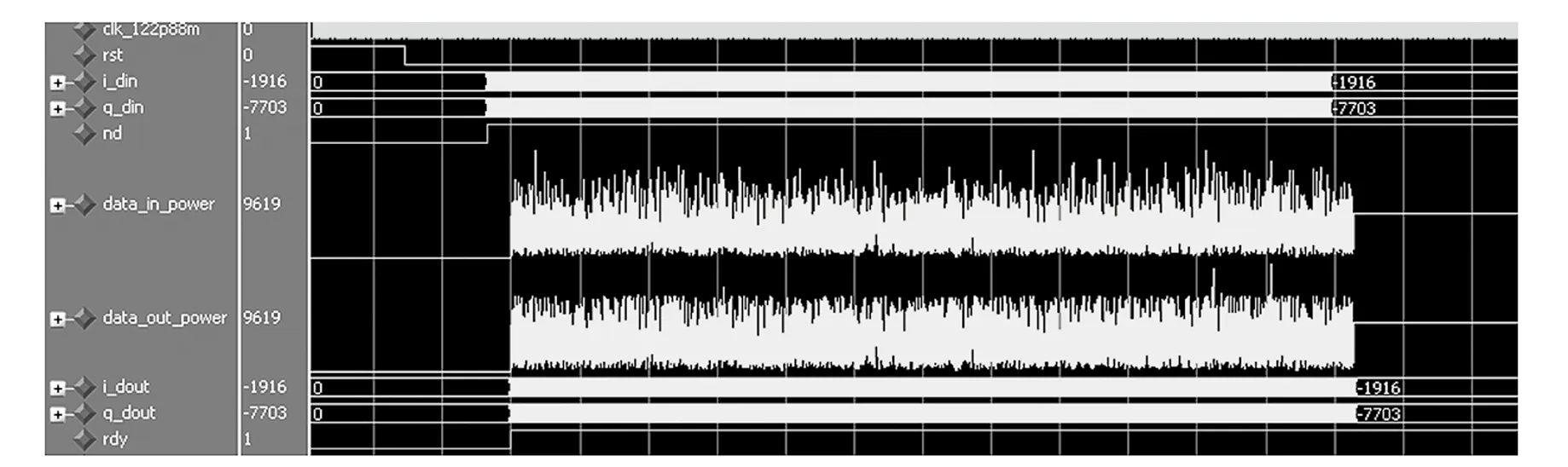
图16 门限值为5 dB时ModelSim输出时域图

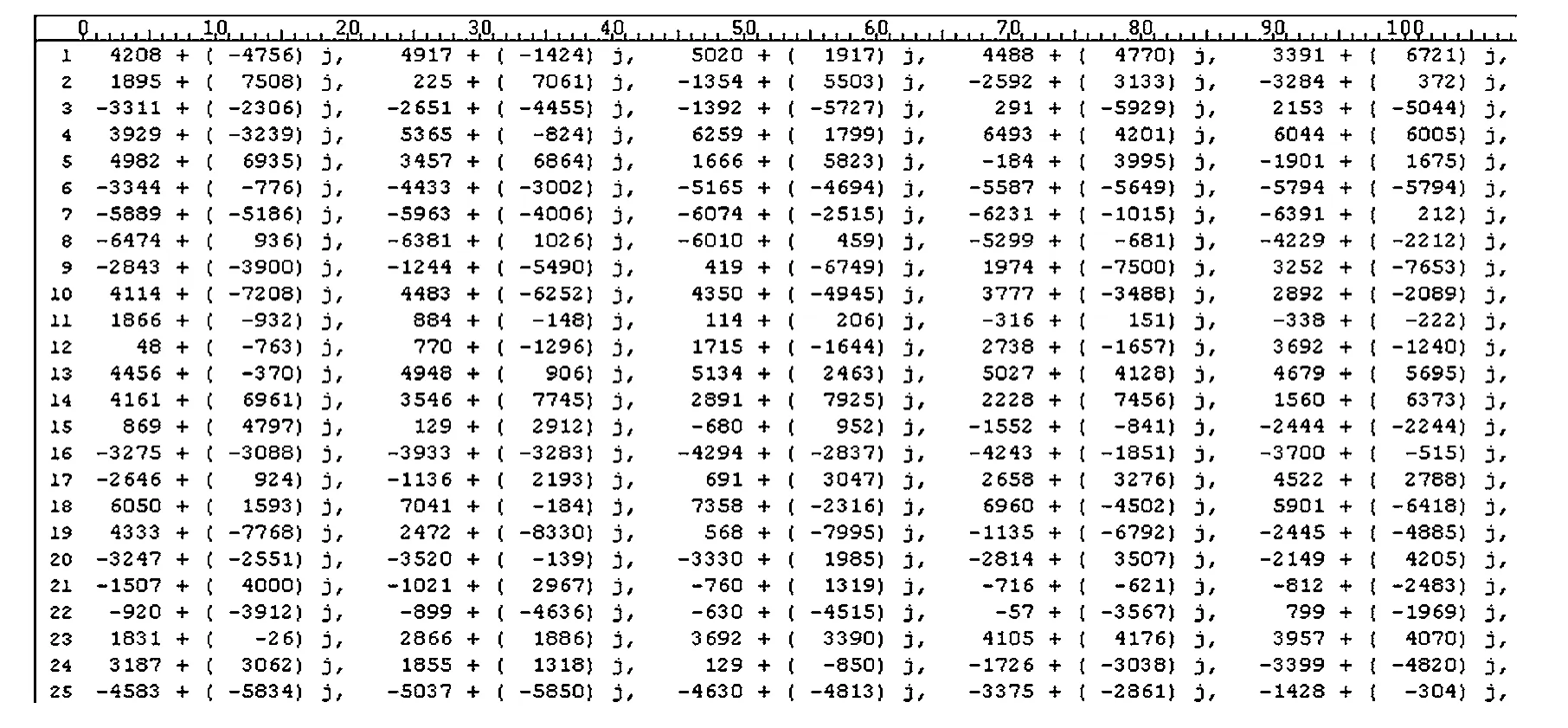
图17 门限值为5 dB时ModelSim输出数据

（2）峰均比抑制门限为7 dB

门限为7 dB时的MATLAB仿真结果如图18和图19所示。其中图18（a）是该抑制算法经过第1次迭代后的时域数据仿真图，图18（b）是该抑制算法经过第2次迭代后的时域数据仿真图。从图中可以看出，算法在第1次迭代后就几乎将超过门限值的信号完全抑制掉了；算法在经过第2次迭代后，未有超过门限阈值的峰值信号出现。所以，算法采用2次迭代，是完全将峰值信号抑制在7 dB门限值以下的。同时多次迭代后也未出现峰值再生的问题，对系统的信噪比几乎没有任何影响[8]，不会恶化整个系统的性能。图19是MATLAB仿真输出的部分数据。

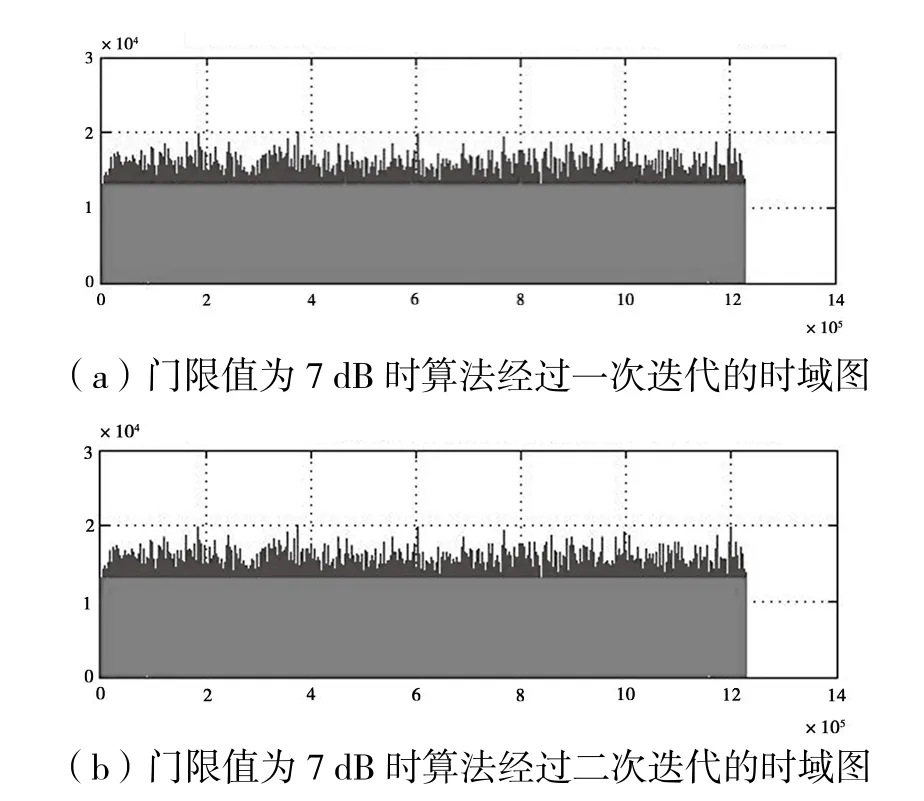
图18 门限值为7 dB时MATLAB时域仿真图

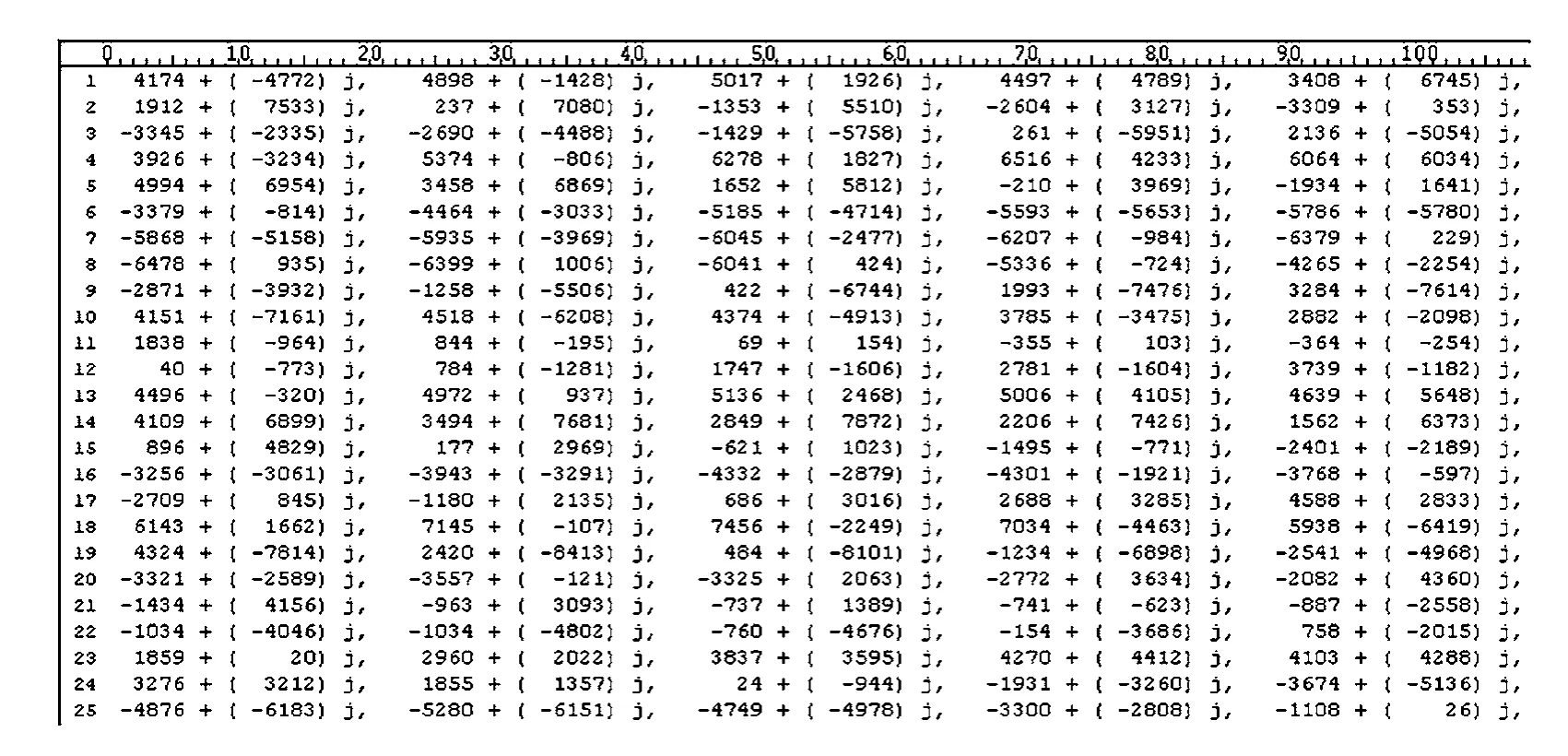
图19 门限值为7 dB时MATLAB仿真输出数据

该算法的FPGA实现模块采用ModelSim软件仿真的结果如图20、图21所示。在图20中显示的时域数据图是第1次迭代和第2次迭代后的算法输出结果。从图20中可看出，7 dB抑制门限的削峰算法在第2次迭代后没有超过7 dB的峰值出现。该结论与MATLAB仿真结果是一致的。

图21是ModelSim仿真输出的部分数据，通过对比图19和21中的数据，发现两组数据完全相同，从而证明了算法FPGA实现与MATLAB仿真达到了完全一致的效果，从而证明了实现的正确性。

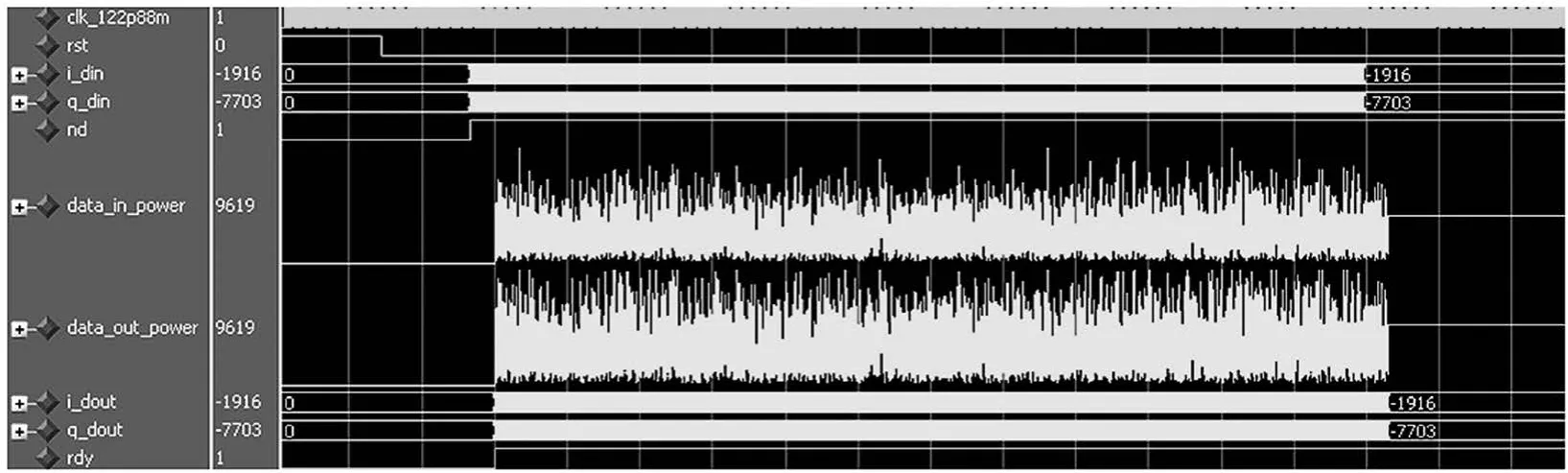
图20 门限值为7 dB时ModelSim输出时域图

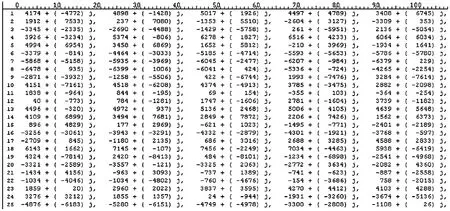
图21 门限值为7 dB时ModelSim输出数据

4 结 语

通过对PC-CFR算法进行原理分析、仿真和FPGA设计实现，证明了该算法的可实现性。使用MATLAB和ModelSim仿真软件，对算法按照设定的不同抑制门限值进行了仿真验证，同时将Modelsim仿真的结果与MATLAB仿真结果进行了对比。从比较的结果可看出，该算法的FPGA实现与MATLAB仿真达到了相同的抑制效果。该算法以较低的失真度，通过多次迭代可有效的将OFDM系统中的峰均比抑制到设定的门限值以下，该算法具有优秀的峰均比抑制效果，在实际工程中具有广泛的应用前景。