L/M倍抽样率转换器及其实现结构*

陈绍荣，刘郁林，李晓毅，徐 舜

（1.陆军工程大学通信士官学校，重庆 400035；2.重庆市经信委，重庆 400015）

0 引 言

在国内外《数字信号处理》教材及著作[1-2]中，从不同角度介绍了实现抽样频率转换的方法，归纳起来有三种实现抽样频率转换的方法：一是若原模拟信号xa(t)可以再生，或是已经记录下来，那么可以重新抽样；二是将x(n)通过D/A变换成模拟信号xa(t)后，对xa(t)经A/D再抽样；三是发展一套算法，对抽样后的数字信号x(n)在“数字域”作抽样率转换，以得到新的抽样。方法一有时不能实现，方法二要再一次受到D/A和A/D量化误差的干扰，方法三是最理想的方法。减少抽样率以去掉多余数据的过程称为序列的重排；增加抽样率以增加数据的过程，称为序列的插值。本文讨论插值器和重排器相结合，以实现L/M倍抽样率转换器的方法。

1 插值滤波器

首先来研究序列的插值与抽样率的关系，再介绍插值滤波器。

1.1 序列的插值与抽样率的关系

设周期为L的周期冲激序列为

以均匀间隔T对连续时间信号xa(t)抽样，得到序列x(n)=xa(nT)，若希望将抽样率fs增加L倍，即变成Lfs，则最简单的方法是对x(n)插值，用符号表示，即

式（2）表明，对序列x(n)插值，等价于将连续时间信号xa(t)的抽样间隔变成T/L，即抽样率变成Lfs。

1.2 插值滤波器

考虑到式（1），对式（2）两边取DTFT，可得插值序列f(n)的频谱，即

式（3）表明，插值序列f(n)的频谱F(ejω)是序列x(n)的频谱X(ejω)压缩L倍的结果。换言之，在F(ejω)的主值区间 [-π,π]上，谱图重复出现了L次，多余的L-1次称为X(ejω)的映像。当|ω|≤π/L时，F(ejω)单一地等于X(ejLω)，我们可以利用后置数字低通滤波器来完成这一任务，如图1所示，其中，后置数字低通滤波器的频率特性为

式中，C为常数，G2π/L(ω)=ε(ω+π/L)-ε(ω-π/L)，ε(ω)为单位阶跃函数。

图1 插值后的滤波

考虑到式（3）及式（4），则后置数字低通滤波器的输出序列y(n)的频谱为

考虑到式（5），则有

考虑到式（6），则有

由式（7）可知，为保证y(0)=x(0)，则应取C=L，于是式（4）可写成

通常将图1所示的插值器后置数字低通滤波器的级联结构，称为插值滤波器。由式（5）所揭示的输出与输入的频率关系可知，该插值滤波器不仅实现了L倍的抽样率转换，而且还滤除了输入序列x(n)的频谱X(ejω)的L-1 次映像。

2 重排滤波器

首先来研究序列的重排与抽样率的关系，再介绍重排滤波器。

2.1 序列的重排与抽样率的关系

以均匀间隔T对连续时间信号fa(t)抽样，得到序列f(n)=fa(nT)，若希望将抽样率fs减小M倍，即变成fs/M，则最简单的方法是对f(n)重排，用符号表示，即

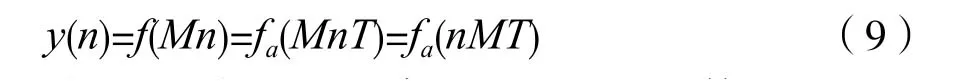
式（9）表明，对序列f(n)重排，等价于将连续时间信号fa(t)的抽样间隔变成MT，即抽样率变成fs/M。

2.2 重排滤波器

考虑到式（1），则有

考虑到式（10），对式（9）两边取DTFT，可得重排序列y(n)的频谱，即

考虑到式（11），则有

式（12）表明，重排序列y(n)的频谱Y(ejω)任然是周期为2π的周期函数。

由式（11）可知，重排序列y(n)的频谱Y(ejω)是序列f(n)的频谱F(ejω)先作M的扩展，再将ω轴上每隔 2π的频移F(ej(ω-2πk)/M)叠加除以M。即重排序列y(n)的频谱Y(ejω)，在一周期2π内的谱图是由M个F(ej(ω-2πk)/M)(k=0,1,2,…,M-1)叠加除以M构成的，因此Y(ejω)中存在频谱重叠。

为使重排序列y(n)的频谱Y(ejω)不出现重叠，一种有效的方法是将序列f(n)的频谱F(ejω)位于主值区间[-π,π]上的部分限制在子区间之内，可以利用前置数字低通滤波器H2(ejω)来完成这一任务，如图2所示，其中，前置数字低通滤波器的频率特性为

式中

其中，ε(ω)为单位阶跃函数。

图2 重排前的滤波

在图2所示的重排滤波中，设频率特性为H2(ejω)数字低通滤波器的单位冲激响应为h2(n)，则有

由于序列f(n)的频谱F(ejω)是周期为2π的周期函数。对式（15）两边取DTFT，并注意到式（13），可得前置数字低通滤波器的输出序列s(n)的频谱，即

考虑到式（11）及式（16），则重排序列y(n)的频谱为

式中

由式（18）可知，Y0(ejω)的最高频率不超过π，因此，按式（17）对Y0(ejω)作周期2π延拓时，重排序列y(n)的频谱Y(ejω)将不会出现重叠。

通常将图2所示的重排器前置数字低通滤波器的级联结构，称为重排滤波器。由式（17）及式（18）所揭示的输出与输入的频率关系可知，该重排滤波器不仅实现了1/M倍的抽样率转换，而且还保证了输出序列y(n)的频谱Y(ejω)不出现重叠。

3 L/M倍抽样率转换器及其实现结构

对于给定的序列x(n)，若希望将抽样率变换成L/M倍，可按前面介绍的方法，先将x(n)做M倍的重排，再做L倍的插值来实现，或是先做L倍的插值，再做M倍的重排来实现。一般来说，重排使x(n)的数据减少，会产生信息丢失。因此，合理的方法是先对序列x(n)做插值，然后再做重排，如图3所示。

在图3中，插值和重排工作在级联状态，两个数字低通滤波器所处理的序列的抽样率都是Lfs，因此，可将它们合起来变成一个数字低通滤波器，如图4所示，这样就构成了一个插值器和重排器相结合的抽样率转换器。

图3 插值与重排的级联实现

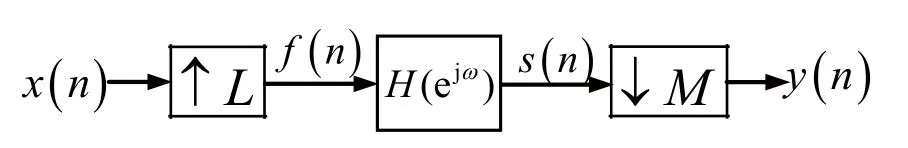
图4 插值器与重排器相结合的抽样率转换器

考虑到式（8）及式（13），则图4中的数字低通滤波器的频率特性为

式中

3.1 L/M倍抽样率转换器的输出与输入的频谱关系

考虑到式（3）和式（19），则有

考虑到式（21），则式（11）可写成

式中

3.2 L/M倍抽样率转换器的输出与输入的时域关系

在图4描述的L/M倍的抽样率转换器中，插值器的输出序列可以表示为

考虑到式（24），则数字低通滤波器的输出序列可以表示为

考虑到式（25），则重排器的输出序列可以表示为

令

从式（29）可以看出，y(n)可以看作是将x(n)通过一个时变滤波器所得到的输出。该时变滤波器的单位冲激响应为

考虑到式（30），则有

由式（31）可知，g(i,n)是以n为变量，周期为L的周期序列。

3.3 L/M倍抽样率转换器的实现结构

由图4描述的L/M倍抽样率转换器可看出，实现L/M倍的抽样率转换需要一个插值器、一个数字先将x(n)每低通滤波器和一个重排器。插值器两位之间插入L-1个零值位，得到f(n)，然后利用数字低通滤波器滤除F(ejω)在区间 [-π/L,π/L]以外由X(ejω)所产生的映像，得到s(n)，最后通过重排器将序列s(n)中相距M位的序列值抽取出来进行重排，得到输出序列y(n)。现在我们要将插值、滤波及重排过程结合起来统一考虑，以实现乘法次数最少的滤波器结构。

为了保证线性相位，数字低通滤波器h(n)可用FIR数字低通滤波器来实现。设h(n)=h(N-1-n)，N取L的整倍数，即N=KL，由式（30）可知，在插值器和重排器相结合的L/M倍的抽样率转换器中，多相数字滤波器的单位冲激响应为

式中，i=0,1,2,…,K-1，n=0,1,2,…,L-1，K=N/L，并且N/L为正整数，N为h(n)的长度。

若N=30，L=5，M=2，则K=6，多相数字滤波器的系数g(i,n)分别是

若采用多相数字滤波器结构，则式（29）可写成

现结合式（39）来讨论插值器和重排器相结合的L/M倍抽样率转换器的工作原理。

根据给定的M、L，设计一个FIR数字低通滤波器h(n)，使之逼近式（19）所描述的理想数字低通滤波器的频率特性，即

当N=30，L=5，M=2时，该抽样率转换器实现L/M=2.5倍的抽样率转换，由式（39）可知，该抽样率转换器的输入数据x(n)的序号按转换，输出序列y(n)的值分别是

分析表明：

（1）利用式（32）的下标映射关系，长度为N的FIR数字低通滤波器h(n)分成L组的子FIR数字滤波器g(i,n)，其中，i=0,1,2,…,K-1，n=0,1,2,…,L-1，而每个子数字滤波器的长度都为K。

（2）对输出y(0)、y(1)和y(2)，使用的是同一组输入数据块x(-i)；对输出y(3)和y(4)，也是使用同一组输入数据块x(1-i)。对输出y(n)，n每变化一次，输入数据块的序号按进行转换。

根据以上特点，并考虑到式（39），可得到图5所示的L/M倍抽样率转换器结构，其中，g(i,n)是以n为变量，周期为L的周期序列，即满足g(i,n+kL)=g(i,n)，并且g(i,n)=h(iL+L)。

当在计算机上实现L/M倍的抽样率转换时，图5的结构形式可以进一步画成图6所示的示意图。该图中输入缓冲器长度为M，中间缓冲器长度为K，数字滤波器系数缓冲器共有L个，每个长度也为K，输出缓冲器长度为L。

图5 L/M倍抽样率转换器的计算机程序

图6 实现L/M倍抽样率转换器的计算机程序方块图

对每一个输出数据块y(n)(n=0,1,2,…,L-1)，在每一个时刻n，一个子滤波器的K个系数和中间缓冲器的K个数据对应相乘，然后相加，得到该时刻的y(n)，用下一个滤波器的系数和中间缓冲器数据对应相乘，再相加，得到下一位输出y(n)。对输出y(n)，n每变化一次，当且仅当递增1时，从输入缓冲器移一个数据到中间缓冲器，当L个输出结束时，应移进=M个数据。如此重复，直到对x(n)的全部数据处理结束。

4 结 语

建立在多抽样率转换理论基础上的多抽样率数字信号处理，已成数字信号处理这一学科中的重要内容，在语音及图像压缩的子带编码得到了广泛的应用。本文对插值器和重排器相结合的L/M倍抽样率转换器的原理进行了详细分析，不仅给出了一种基于时变滤波器组的L/M倍抽样率转换器的实现结构，而且还给出了实现L/M倍抽样率转换器的计算程序方框图。