组合证券投资决策分析

孙 明，汪 玮

(安徽财经大学 会计学院,安徽 蚌埠233030)

1 背景分析

1952年，Markowitz在其《组合证券选择》中正式提出了组合证券投资决策理论[1]42。其理论主要包括均值-方差分析法和投资组合有效边界模型，被广泛用于经营过程中组合的选择和资产的配置。而在组合证券投资决策理论形成之前，对于如何将投资风险降到最低已经得到了投资者的广泛关注，Hicks提出了“分离定理”[1]43，解释了投资者获得高收益、低风险的期望并且将风险引入投资分析中；Williams提出了“分散折价模型”[1]43，使投资的组合证券很好地规避了风险，并假设始终存在一个收益最大化和风险最小化的投资方式。而对于Markowitz提出的理论，最值得关注的是其中包含的三个假设：一是投资者期望规避风险，追求利益的最大化；二是投资者根据预期收益率的期望值和方差来进行投资组合；三是构建投资者都处在同一单期投资期这一理想化情景。

2 模型分析

根据Markowitz的设想，投资收益率可以被看作是一个随机变量X，同时可以用一定时期内的某种证券收益率的期望值E(X)来代表该种证券投资的获利能力的大小。但是，由于证券市场受到许多不同因素的影响而具有不确定性，可以用证券收益率的方差D(X)来衡量该证券的风险，方差越小，说明证券投资的风险越小。

假设投资者选了n种债券进行投资，Xi代表在证券投资期间第i种证券的收益率，投资者自身的预期收益和预期风险分别用Xi的数学期望E(Xi)=μi和方差D(Xi)=λ2i(i=1,2,3…n)表示。n种证券收益可以表示为X=(X1,X2,…,Xn)T,它的数学期望可以表示为μ=(E(X1),E(X2),…,E(Xn))T=(μ1,μ2,…μn)T，假设其协方差矩阵为正定矩阵，则其可以表示为:

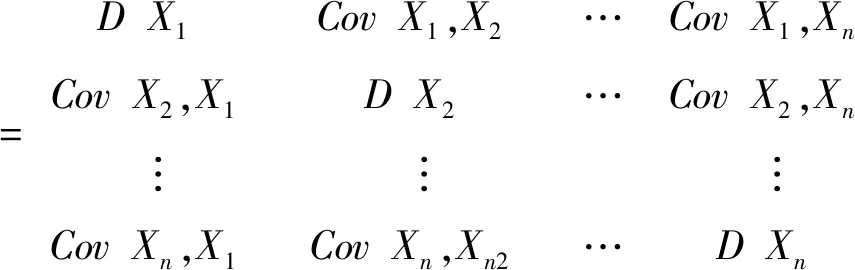
(式1)

组合证券投资收益率为:

(式2)

组合证券投资的数学期望为：

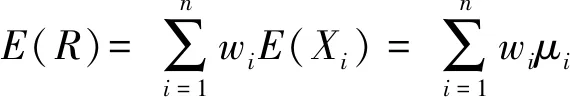
(式3)

方差为:

(式4)

式3中,λij表示第i种和第j种证券投资的协方差，反映了二者之间的相关程度，且λij=λji，λii=λ2i(i，j=1,2,…,n)。

假设W=(w1,w2,…,wn)T和FTn=(1,1,…,1)是分量全为1的n维向量，则证券投资组合的收益和风险分别为:

e=WTμ

(式5)

λ2=WTMW

(式6)

由式5、式6可知，在选择n种证券进行组合投资时，投资者的预期收益μ0和协方差矩阵M都可以通过计算得到，所以组合证券投资的e和λ2，即收益和风险是由投资者对于n种证券的投资比例决定的。而对于投资者而言，最佳的理想状态是收益最大、风险最小，即maxe=WTμ和minλ2=WTMW，但二者兼顾显而易见是很难做到的，只能做到尽可能地保持二者的平衡，在承担一定的风险的情况下获得理想的收益，由此，可建立模型：

minλ2=WTMW

(式7)

由式7可知，在预期收益不小于μ0的情况下，投资风险最小。运用此模型不仅可以解决不同类型的证券组合，对于同类但不同收益率的证券同样适用[2]。例如：以下选取在A股已经上市的上证、深证以及创业板的3只股票，根据2018年3月至8月收益率的变化情况，进行组合证券投资分析。详情见表1—表3。

表1 贵州茅台2018年3月至8月收益率

表2 张江高科2018年3月至8月收益率

表3 格力电器2018年3月至8月收益率

第m种证券第n期的收益可以表示为xnm，由表1—表3可以得到以下样本数据(见表4)。

表4 3只股票收益率汇总情况

由表4可计算出预期收益μ和协方差矩阵M分别为：

μ=(16.36%,11.61%,18.44%)T

假设进行组合证券投资决策时，投资者的预期收益率不得低于18%，即在投资收益不低于18%的前提下，使投资风险最小，代入数据得：

用LINGO10.0进行求解得：

w1=0.2056

w2=0

w3=0.7944

minλ2=1.401990

三只股票收益率变化如图1所示。

图1 3只股票收益率变化情况

结合3只股票的收益变化可以得出，股票1的投资比例为20.56%，股票2的投资为0%，股票3的投资为79.44%。由此可见，假定投资者的预期收益率为18%，张江高科由于收益率较预期偏差大，在进行投资时将其排除在外，而格力电器与贵州茅台将其收益率与风险组合搭配，使得最终的收益率不小于15%[3]。

Markowitz提出的均值-方差分析模型也存在许多局限性，主要体现在实际运用之中。首先，均值-方差分析模型需要计算所投资证券预期收益率的数学期望、方差和证券之间的协方差，但在实际操作过程中，证券的数量较多，数据整理和收集的工作量十分巨大，求解过程也十分困难；其次，在求解过程中难免存在误差，可能求出的结果不是最佳投资组合；最后，交易存在根据均值-方差分析模型频繁调整投资比例时，往往会面临数额巨大的交易费用，所以投资者在进行投资决策时，往往会维持现状，而不会按照最新计算的结果对证券投资的比例进行调整[4]。

3 决策分析

对于投资者来说，他们所追求的目标永远都是投资收益的最大化或投资回报率的最大化，即期望值E(X)最大。但是，投资的同时必然伴随着风险，即方差D(X)的存在，通过模型分析可以得出投资收益与风险呈正相关关系，投资收益越高意味着风险越大。所以，投资者在可以接受的既定风险范围内选择收益最大化的投资决策。

投资的主要风险有流动性风险，申购、赎回价格未知风险和证券投资风险。其中，流动性风险等价于投资者持有金融资产的变现难易程度，在企业中是指本企业不能获得足够的资金来归还到期负债的风险。作为投资者则要清楚地了解该企业的经营状况和偿债能力等，降低流动性风险，降低方差D(X)的值。申购、赎回价格未知风险，即投资人在申购、赎回证券时所参考的价格是上一个交易日的价格，所以投资者要承担当日证券净值不确定的风险。证券投资风险是源于投资活动中的时空差和收益差，同时由于投资者对投资理财产品的认识有限和产品本身的缺陷，以及所掌握的信息不对称和投资过程中的失误，造成投资与预期的结果相偏离，使得方差D(X)的值升高。

投资者所获得证券投资收益，首先是证券净值的增长，即差价获利。其中，一部分来自低价买进高价卖出所赚取的证券差价收益，另一部分来自持有的未卖出的有价证券在账面上可以看到的增值利润。其次是证券的收益分配，包括利息收入和股利收入。二者共同影响期望值E(X)的大小。

因此，在进行决策分析时，要把握期望值E(X)和方差D(X)的影响因素：一是从单个因素进行决策，单向选择期望值较高、方差较低的几类证券，设计投资方案；二是结合投资主体自身的需求，确定合理的投资预期比例μ0的大小，套用数学模型求解，得出最佳的投资组合比例；三是结合投资者的实际情况，对原有的设计方案作出调整。

4 案例分析

中国人寿保险股份有限公司是一家国有特大型金融保险企业，其通过保费的收入获得大量资金。该公司是我国资本市场中最大的机构投资者之一，其在投资过程中坚持在既定的风险范围内保证获益最大这一组合证券投资决策原则。以下以中国人寿保险股份有限公司2017年度的组合投资资产为例，分析组合证券投资决策对于该企业的影响。详情见表5。

表4 中国人寿保险股份有限公司2017年度财务报告投资项目附注 单位：百万元

数据来源：中国人寿保险股份有限公司2017年年度财务报告。

分析表5的数据可知，该公司在2016年和2017年所作的组合投资决策是不同的。该公司在2017年中增加了债权型投资，降低了D(X)。同时，该公司还减少了股权型投资，其中，对股票和优先股的投资额仍然有所增加，主要减少了对基金的投资。但是，无论是债权型投资还是股权型投资，其中理财产品的投资额均是大幅度的缩减。这可能与当时理财产品市场的过度膨胀而后又快速削减的情况有关，许多理财产品的收益率急剧下降，导致投资者自身的μ0有所下降。从纵向对比来看，该公司的债权型投资的投资额高于股权型投资的投资额。说明该公司偏向于稳健型的投资，即采用E(X)和D(X)相对均衡的投资模式。一般来说，债券型投资的收益率和风险较低，而股权型投资的收益率和风险较高。因为两者具有负相关性，所以它们相互结合可以有效降低风险和提高收益率。通过以上分析可以得出结论：在一定的风险水平上，公司的组合投资决策的收益率大于或等于该公司的期望收益，该组合投资是有效的。

从中国人寿保险股份有限公司持续发展这一案例可以发现，对于投资者自身而言，一定要选择在自己预期的可接受风险范围内的合适的投资方式；对于风险偏好者来说，可以适当提高收益高的证券的投资比例，而那些承受风险能力较差的投资者则需要考虑风险和收益的关系，理性投资，不盲目追求过高的收益;对于企业来说，可以选择比较稳健的组合投资方式。企业的发展离不开投资和融资，选择适合自身发展的组合投资方式至关重要。

5 结语

综合上述分析，由于投资理财产品越来越多样化，投资者在选择投资项目或产品进行组合性投资时，一定要注意其中的相关性，尽量选择相关程度较小或者负相关的多种证券组合投资。