借力函数思想 巧解数列问题

■浙江省丽水中学 周杰华

数列是高考数学的核心知识,经常采用“一大一小”的形式考查数列的概念、基本方法和重要思想。在人教版必修5的课本中有这么一段话：“你能从函数的观点认识数列吗? 数列实际上是定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数当自变量从小到大依次取值时对应的一列函数值。”一般地,等差、等比数列与函数的联系如下图所示。

下面谈谈从函数的视角研究解决数列问题,如等差、等比数列的通项公式及性质,数列中的单调性、有界性与最值、数列不等式等。

一、运用函数模型解题

例1已知等差数列｛an｝,SP=q,Sq=p(p≠q),求Sp+q。

解析：因为是关于n的一次函数,所以当n∈N*时,点共线。

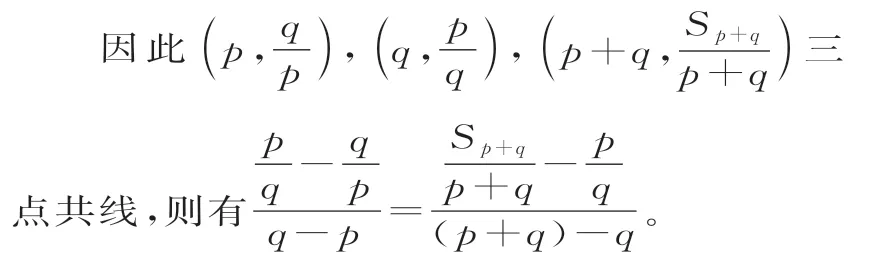
化简得：

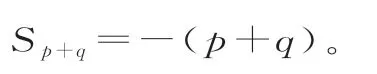
例2(1)已知正项数列{an}的前n项和为Sn,若{an},{}分别是公差为d,的等差数列,则an=_____；Sn=____。

(2)两个等差数列{an},{bn}前n项和分别为An,Bn,满足

解得a1=1,d=2。

所以an=2n-1,Sn=n2。

(2)由题意可设An=an(7n+2),则Bn=an(n+3)。

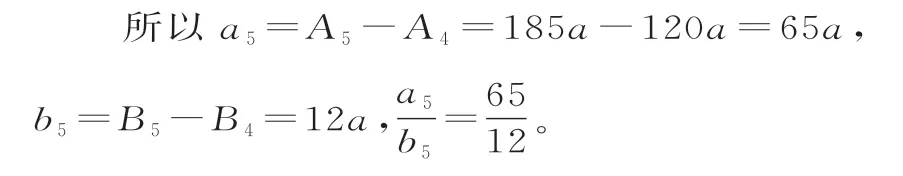
点评：借助等差数列前n项和是常数项为0的二次函数这一特点来研究等差数列有关项与和的问题,在解题过程中利用这一特点能使问题简单化。

二、运用函数性质解题

例3设函数f(x)=2x-cosx,{an}是公差为的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2-a1a5=( )。

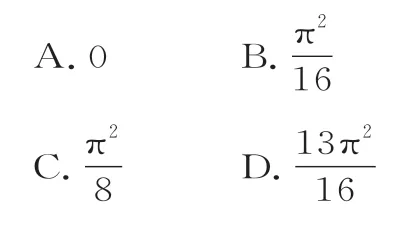
解析：因为f(a1)+f(a2)+…+f(a5)=5π,所以2(a1+a2+a3+a4+a5)-(cosa1+cosa2+cosa3+cosa4+cosa5)=5π。

构造函数g(x)=2x-sinx,g(x)是在R 上单调递增的奇函数。

又因为{an}是公差为的等差数列,所以a3-=0,即a3=

故[f(a3)]2-a1a5=,选D。

点评：本题考查函数和数列的综合运用,运用等差数列的性质和函数的奇偶性是解题的关键。

三、函数思想的深度应用

例4设a,b∈R,数列{an}中a1=a,,n∈N*,则( )。

A.当b=时,a10＞10

B.当b=时,a10＞10

C.当b=-2时,a10＞10

D.当b=-4时,a10＞10

解析：令f(x)=x2+b,an+1=f(an)。

选项B,当b=时,由x2+=x,得x=,即x=为函数f(x)=x2+b的不动点。若a=,此时an=,a10＜10,不合题意。

选项C,当b=-2时,由x2-2=x,得x=2或-1,即x=2或-1为函数f(x)=x2+b的不动点。若a=2,则an=2＜10不合题意。

选择D,当b=-4时,由x2-4=x,得x=,即x=为函数f(x)=x2+b的不动点。

若a=,则an=＜10,不合题意。

所以选A。

点评：本题给出了首项与递推关系,既不是等差数列也不是等比数列,因此无法从常规的基本量入手分析。像这类二次递推数列,若能从函数图像入手即从比较直观的角度观察数列的迭代变化,也就是我们常说的借助蛛网法研究数列的不动点问题。

例5已知各项均为正数的等比数列{an},各项均为正数的数列{bn},满足：an+1=,n∈N*。

(1)证明：数列{an}是常数列；

解析：

又因为{an}为等比数列,所以数列{an}是常数列。

(2)由(1)知{an}为常数列,不妨设an=a1=a＞0。

从(*)式可以看出,bn至多两项,正项等比数列{bn}有界且不趋于0,所以数列{bn}的公比=1,a=。代入(*)式得+2=0,即(bn-)2=0,bn=。

所以数列{an}和{bn}都是各项为的等比数列,故

点评：本题以等比数列为背景,给出一个递推关系,数列的基本量无法确定,因此需要改变角度,从式子的整体结构出发,结合等比数列的性质去求解。本题从函数的角度来看等比数列,即一正项等比数列若有界,则该等比数列必为常数列,另外也还体现了整体思想与方程的思想。