精讲解三角形考点

■河南省禹州市第一高级中学 田治业

高考有关解三角形的考题形式为选择题、填空题或解答题,主要考查利用正弦定理、余弦定理、三角公式、三角函数图像与性质解三角形及求三角形的面积,解实际问题,求平面图形中的边角关系,求与三角形有关的最值、取值范围等综合问题,难度为基础题和中档题。

考点一、已知三角形中的边角关系解三角形

1.对已知三角形的边角关系解三角形问题,若所给条件含边又含角,要么把角化为边,要么把边化为角。

2.若条件给出三角形面积,则利用三角形面积公式化为边角问题处理。

3.若以向量运算的形式给出条件,则利用向量运算的相关知识化为边角关系,再利用余弦定理求解。

4.在利用正弦定理解题时,应注意利用大边对大角来判断所求角的范围。

5.三角形中的三角变换：

(2)在△ABC中,熟记并会证明：A,B,C成等差数列的充分必要条件是B=60°；△ABC是正三角形的充分必要条件是A,B,C成等差数列且a,b,c成等比数列。

6.要熟记如下知识：

(1)正弦定理：

(2)在三角形中,大角对大边,大边对大角；大角的正弦值也较大,正弦值较大的角也较大,即在△ABC中,A＞B⇔a＞b⇔sinA＞sinB。

(3)在△ABC中,已知a,b和A时,解的情况如下：

(4)余弦定理：

例1在△ABC中,。

(1)求B的大小；(2)求的最大值。

分析：(1)根据余弦定理公式求出cosB的值,进而根据B的取值范围求B的大小；(2)由辅助角公式对进行化简变形,进而根据A的取值范围求其最大值。

解：(1)由余弦定理及题设得cosB=

又因为0＜B＜π,所以B=。

(2)由(1)知A+C=。

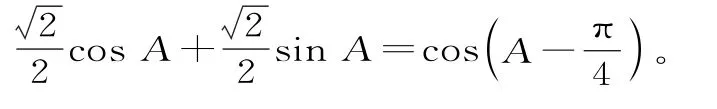
因为0＜A＜,所以当A=时,cosA+cosC取得最大值1。

点评：正弦、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据。其主要方法有：化角法,化边法,面积法,运用初等几何法。注意体会其中蕴含的函数与方程思想、等价转化思想及分类讨论思想。

考点二、利用正弦定理、余弦定理解平面图形问题

对解平面图形中的边角问题,若在同一个三角形中,可直接利用正弦定理与余弦定理求解。若图形中条件与结论不在同一个三角形内,思路1：要将不同的三角形中的边角关系利用中间量集中到一个三角形内列出在利用正余弦定理列出方程求解；思路2：根据图像分析条件和结论所在的三角形,分析由条件可计算出的边角和由结论需要计算的边角,逐步建立未知与已知的联系。

例2在△ABC中,点D在BC边上,AD平分∠BAC,AB=6,AD=,AC=4。

(2)求BC的长。

分析：(1)由正弦定理知,在△ABD中,①；在△ADC中,②。由∠ADB+∠ADC=π,∠BAD=∠DAC,得sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC,然后再由①÷②即可得到结果。(2)由(1)知,设BD=3x,DC=2x(x＞0),则BC=5x。由cos∠BDA+cos∠ADC=0及余弦定理知0,由此即可求出结果。

解：(1)由正弦定理知,在△ABD中,

由∠ADB+∠ADC=π,∠BAD=∠DAC,得 sin ∠ADB=sin ∠ADC,sin∠BAD=sin∠DAC。

由cos∠BDA+cos∠ADC=0,及余弦定理知。

解得x=1,所以BC=5。

考点三、利用正弦定理、余弦定理解测量,航行问题

1.把握解三角形应用题的四步：

①阅读理解题意,弄清问题的实际背景,根据题意画出示意图；

②根据图形分析图中哪些量是已知量,哪些量是未知量,需要通过哪些量将未知与已知沟通起来,将实际问题抽象成解三角形问题的模型；

③根据题意选择正弦定理或余弦定理求解；

④将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等。

2.要理解仰角和俯角、方位角、方向角的概念,并能将其化为三角形内角。

例3为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测。如图1所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100 m,∠BAC=60°,在A地听到弹射声音比B地晚(已知声音传播速度为340 m/s),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=____。

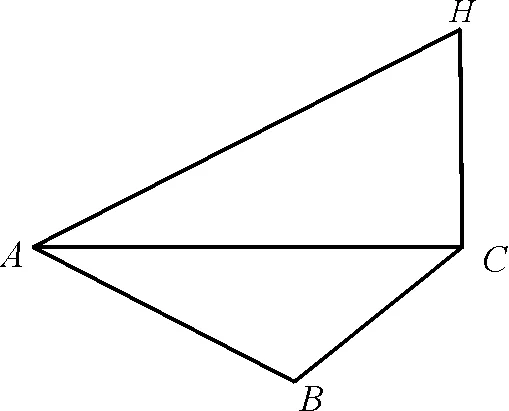
图1

分析：在图中标注出已知量,分析所求量与已知量的关系,在三角形中利用正弦定理与余弦定理求解。

解：设BC=x,则AC=x+×340=x+40。在△ABC中,由余弦定理,可得BC2=AB2+AC2-2AB×ACcos∠BAC,即x2=1002+(40+x)2-2×100×(40+x)×,解得x=380,所以AC=380+40=420(m)。因为∠HAC=30°,所以∠AHC=90°-30°=60°。

点评：解题中要认真分析与问题有关的三角形,正确运用正、余弦定理有序地解相关的三角形,从而得到问题的答案。