用放缩法证明数列不等式的策略

■河南省信阳市二高 李吉辉

用放缩法证明数列不等式一直是高考及高考备考的一个难点和热点,也是同学们不易掌握,感到难以驾驭的一块知识。主要难在：

(1)放缩的方向在哪里?

(2)放缩的尺度在哪里?

以下谈谈我的心得。

一、总体思想

用放缩法证明数列不等式,总的来说就是已知或可以求出数列的通项公式an,要证明其前n项和Sn＜k(常数),但是Sn无法按常用方法求出,这时就需要用放缩法把an放缩成可以求和的一个新数列。

二、常用的放缩方法

1.根式an=的放缩。

3.分式指数an=(a＞1,k＞0,an-k≠0)的放缩。

4.分式指数an=(a＞1,k＞0)的放缩。

5.分式多项式an=的放缩。

三、类型归纳

1.等比型。

例1已知数列{an}的通项公式an=,前n项和为Sn,证明：Sn＜1。

解析：此题简单,直接用求和公式Sn=,即可。

2.可以放缩为等比型。

例2已知数列{an}的通项公式an=,前n项和为Sn,证明：Sn＜1。

解析：此题要求的精确度不强,可以直接放缩,再用求和公式Sn=,即可。由题中已知条件可得为等差数列。

3.多项式的裂项。

例3已知数列{an}满足an≠0,a1=,an-1-an=2an·an-1(n≥2,n∈N)。

解析：(1)证明数列为等差数列只需按数列定义证明,即证：当n≥2时,为常数即可。

例4(2014 年广东高考卷)设各项均为正数的数列{an}的前n项和为Sn,且Sn满足-(n2+n-3)Sn-3(n2+n)=0,n∈N*。(1)求a1的值；(2)求数列{an}的通项公式；(3)证明：对一切正整数n,有

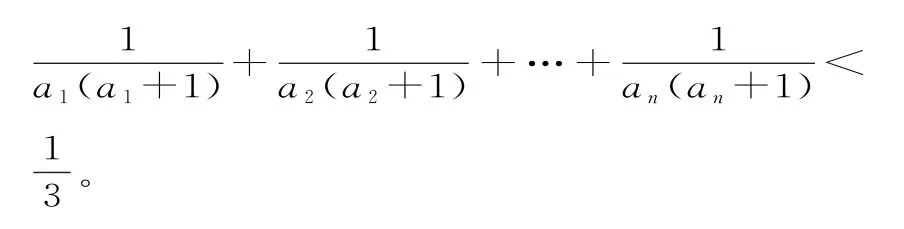
解析：(1)令n=1,代入式子得a1=2或-3(舍去)。

当n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n；

当n=1时,a1=2也满足上式。

所以an=2n,n∈N*。

(3)当k∈N*时,4k2+2k-(3k2+3k)=k2-k=k(k-1)≥0,故4k2+2k≥3k2+3k。

4.指数的放缩。

例5已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*)。(1)求{an}的通项公式；(2)设bn+1=2bn-2n+1,b1=8,Tn是数列{bn}的前n项和,求正整数k,使得对任意n∈N*均有Tk≥Tn恒成立；(3)设cn=,Rn是数列{cn}的前n项和,若对任意n∈N*均有Rn＜λ恒成立,求λ的最小值。

解析：(1)由Sn=2an-2,得Sn+1=2an+1-2。两式相减,整理得an+1=2an+1-2an,an+1=2an,数列{an}为等比数列,公比q=2。由S1=2a1-2,得a1=2a1-2,a1=2。故an=2n。

整理得bn=2n(5-n)。

方法一 当n≤5 时,bn=2n(5-n)≥0,因此,T1＜T2＜T3＜T4=T5＞T6＞…,对任意n∈N*均有T4=T5≥Tn,故k=4或5。

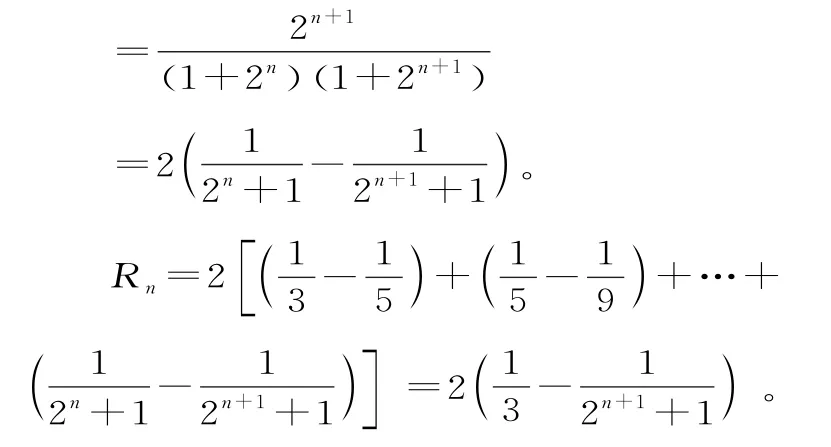
因为对任意n∈N*均有Rn＜成立,所以λ≥,λ的最小值为。

5.需要先准确运算几步,再放缩。

当我们放缩的方法正确,但是无法满足要求时,有可能是放缩的项太多,需要先准确运算几步,再放缩。

例6已知数列{an}的通项公式an=,前n项 和 为Sn。(1)证明：Sn＜1；(2)证明：Sn＜。

解析：(1)第一问比较简单,要求的精确度不强,可以直接放缩,直接用等比数列求和公式＜1,即可。

(2)按照第一问思路时,结果达不到问题的要求,怎么办? 我们先准确运算几步看一看：

原式成立。