全国名校数列测试题（B卷）

■河南省许昌高级中学胡银伟许昌市名师工作室 胡银伟

一、选择题

1.已知数列{an}中,a1=1,n≥2 时,an=an-1+2n-1,依次计算a2,a3,a4后,试猜想an的表达式是( )。

A.an=3n-1 B.an=4n-3

C.an=3n-1D.an=n2

2.已知数列{an}满足a1=1,,则a4=( )。

A.4 B.-4 C.8 D.-8

3.已知公比不为1的等比数列{an}满足a15a5+a14a6=20,若=10,则m=( )。

A.9 B.10 C.11 D.12

4.设等差数列{an}的前n项和为Sn,若2a3+a9=6,则S9=( )。

A.9 B.18 C.27 D.36

5.已知正项等比数列{an}的前n项和为Sn,且7S2=4S4,则公比q的值为( )。

6.已知数列{an}满足a1=1,an+1=,则a100=( )。

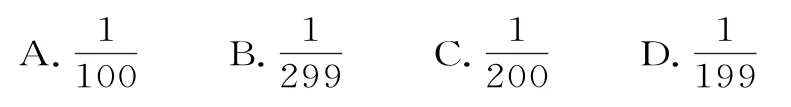
7.在等比数列{an}中,a1a2=1,a5a6=9,则a3a4=( )。

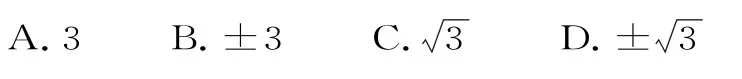
8.已知等差数列{an}的前n项和为Sn,且S4=0,S8=32,则an=( )。

A.4-2nB.3n-9

C.4n-12 D.2n-5

9.已知等差数列{an}的前n项和为Sn,若S3=S12,则a8的值为( )。

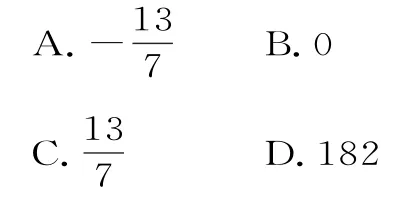
10.设Sn是等差数列{an}的前n项和,若=( )。

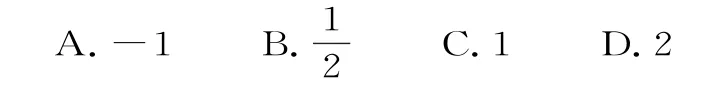
11.已知数列{an}满足a1=,an+1=,则an=( )。

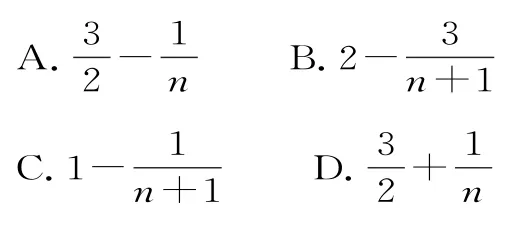
12.在正项等比数列{an}中,a2a7=4,则log2a1+log2a2+…+log2a8=( )。

A.2 B.4 C.6 D.8

13.等差数列{an}的前n项和为Sn,若a8=2,S7=98,则a3+a9=( )。

A.16 B.14 C.12 D.10

14.等差数列{an}中,S16＞0,S17＜0,当其前n项和取得最大值时,n=( )。

A.8 B.9 C.16 D.17

15.各项不为零的等差数列{an}中,,数列{bn}是等比数列,且b7=a7,则b6b8=( )。

A.4 B.8 C.16 D.64

16.已知等差数列{an}的公差不为零,Sn为其前n项和,S3=9,且a2-1,a3-1,a5-1构成等比数列,则S5=( )。

A.15 B.-15 C.30 D.25

17.在公比q为整数的等比数列{an}中,Sn是数列{an}的前n项和,若a1+a4=18,a2+a3=12,则下列说法错误的是( )。

A.q=2

B.数列{Sn+2}是等比数列

C.S8=510

D.数列{lgan}是公差为2的等差数列

18.在一个数列中,如果每一项与它的后一项的和都为同一个常数,则这个数列叫作等和数列,这个数叫作数列的公和。已知等和数列{an}中,a1=2,公和为5,则a18=( )。

A.2 B.-2 C.3 D.-3

19.各项均为正数的等比数列{an}的前n项和为Sn,若S10=20,S30=140,则S40=( )。

A.280 B.300 C.320 D.340

20.已知等差数列{an}的公差为d,若,且b1+b3=17,b2+b4=68,则d=( )。

A.1 B.2 C.3 D.4

21.等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+…+a2n-1)(n∈N*),a1a2a3=-27,则a5=( )。

A.81 B.24 C.-81 D.-24

22.设等差数列{an}的前n项和为Sn,首项a1＞0,公差d＜0,a10·S21＜0,则Sn最大时,n的值为( )。

A.11 B.10 C.9 D.8

23.在a,b中插入n个数,组成等差数列a,a1,a2,…,an,b,则a1+a2+…+an=( )。

24.已知等差数列{an}的前n项和为Sn,a4=4,S5=15,则数列的前2 019项和为( )。

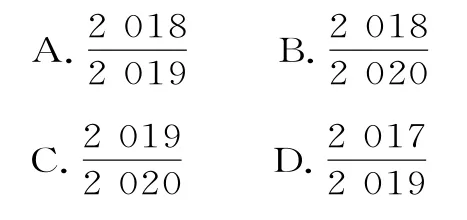
25.已知数列{an}的前n项和为Sn,满足2Sn=3an-1,则通项公式an等于( )。

A.an=2n-1B.an=2n

C.an=3n-1D.an=3n

26.意大利数学家列昂那多·斐波那契以兔子繁殖为例,引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,…,即F(1)=F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3,n∈N*),此数列在现代物理、化学等都有着广泛的应用。若此数列被2整除后的余数构成一个新数列{an},则数列{an}的前2 019项的和为( )。

A.672 B.673

C.1 346 D.2 019

27.等比数列{an}各项均为正数,a3,a5,-a4成等差数列,Sn为数列{an}的前n项和,则=( )。

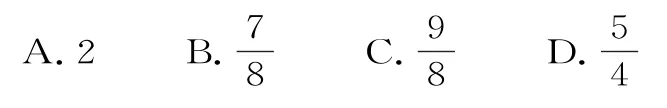
28.等比数列{an}满足a1+a4=,S6=9S3,bn=log2an,则数列{bn}的前10项和是( )。

A.25 B.35 C.-25 D.-35

29.已知正项数列{an}满足a1=1,,则使an＜7 成立的n的最大值为( )。

A.3 B.4 C.24 D.25

30.等差数列{an},{bn}的前n项和分别为Sn和Tn,若=( )。

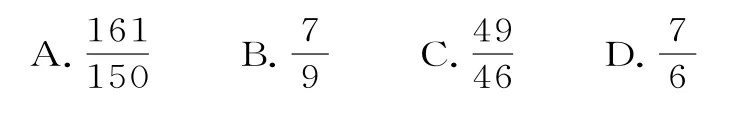
31.设各项均不为零的等差数列{an}的前n项和为Sn,已知a10＞a9,且S10=0,则使不等式成立的正整数n的最小值是( )。

A.9 B.10 C.11 D.12

32.在等差数列{an}中,其前n项和是Sn,若S9＞0,S10＜0,则在中最大的是( )。

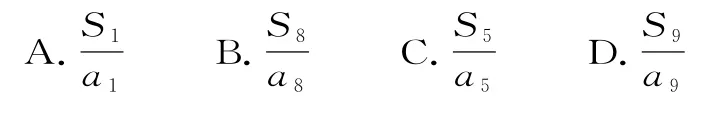
33.设数列{an}的前n项和为Sn,且a1=1,an=+2(n-1)(n∈N*),则数列的前10项的和是( )。

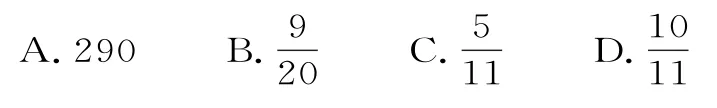
34.若一个数列的第m项等于这个数列的前m项的乘积,则称该数列为“m积数列”。若各项均为正数的等比数列{an}是一个“2 019积数列”,且a1＞1,则当其前n项的乘积取最大值时,n的值为( )。

A.1 010 B.1 009

C.1 009或1010 D.1 008或1 009

35.已知数列{an}满足an=3n+2,bn=5n+3(n∈N*),则在集合M={1,2,3,…,2 019}的元素中,属于数列{an},{bn}的公共项的个数为( )。

A.133 B.134 C.135 D.136

36.已知数列{an}满足2a1+22a2+…+2nan=n(n∈N*),数列的前n项和为Sn,则S1·S2·S3·…·S10=( )。

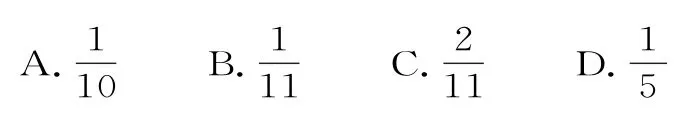
37.已知等比数列{an}的各项均为正数,且满足a2a16=16,,记等比数列{an}的前n项的积为Tn,则当Tn取得最大值时,n=( )。

A.8或9 B.9或10

C.10或11 D.11或12

38.已知正项数列{an}的前n项和为Sn,且a1=1=2Sn+n+1(n∈N*),设数列的前n项和为Tn,则Tn的取值范围为( )。

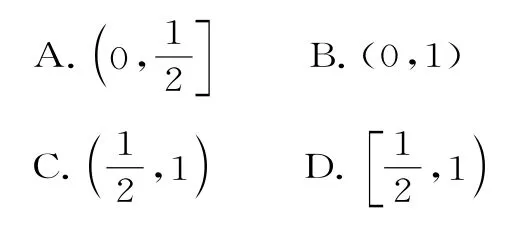
二、填空题

39.已知数列{an}满足a1·a2·a3…an=n+1(n∈N*),则an=____。

40.等差数列{an}中,a3+a10=25,则其前12项之和S12的值为____。

41.已知数列{an}是正项等比数列,且a2·a7=4a5,a4与2a6的等差中项为18,则a5=____。

42.已知数列{an}满足an=2n-1+n,则数列{an}的前6项和为_____。

43.已知数列{an}与均为等差数列(n∈N*),且a1=1,则a10=____。

44.若点(n,an)都在直线y=3x-24上,则数列{an}的前n项和取得最小值时n等于_____。

45.已知数列{an}(n∈N*)是等差数列,Sn是其前n项和,若a2a5+a8=0,S9=27,则S8的值是____。

46.设等比数列{an}各项均为正数,若a4=2,a6=5,则数列{lgan}的前9项和等于____。__

47.已知等差数列{an},满足,其中P1,P,P2三点共线,则数列{an}的前16项和S16=____。

48.已知数列{an}的各项均为正数,记Sn为数列{an}的前n项 和,若an+1=,a1=1,则S7=_____。

49.已知数列{an}的前n项和为Sn,若a1=1,a2=2,(an+1-2n)Sn+1=an+1Sn-1-2nSn(n≥2)。设bn=a2n-1,数列{bn}的前n项和为Tn,则T100=____。

50.若数列{an}是正项数列,且++…+=n2+3n+2(n∈N*),则

51.设数列{an}的前n项和为Sn=3·2n(n∈N*),数列{bn}为等差数列,其前n项和为Tn。若b2=a5,b10=S3,则Tn取得最大值时n=_____。

52.设数列{an}的前n项和为Sn(n∈N*),现有下列三个命题：

①若数列{an}既是等差数列又是等比数列,则an=an+1；

②若Sn=an(a为非零常数),则数列{an}是等比数列；

③若Sn=1-(-1)n,则数列{an}是等比数列。

其中真命题的序号是____。

53.已知数列{an}的前n项和为Sn,若Sn=3an-3,n∈N*,则an=_____。

54.已知正项等比数列{an}的前n项和为Sn,若2S2,S6,4S4成等差数列,且a5=2,则a1=_____。

55.数列{an}的通项公式an=,其前n项和为Sn,则S2019等于____。

56.已知数列{an}的前n项和为Sn,且满足a1=,an+2Sn·Sn-1=0(n≥2,n∈N*),则数列{an}的通项公式an=____。

57.已知数列{an}满足a1=1,an=2an-1+1(n≥2,n∈N*),则数列的最大值为____。

58.已知等差数列{an}的前n项和为Sn,且a2=6,a3+a6=27。设Tn=若对于一切正整数n,总有Tn≤t成立,则实数t的取值范围是____。

三、解答题

59.设Sn为数列{an}的前n项和,已知a1=2,且对任意n∈N*,都有2Sn=(n+1)an。

(1)求数列{an}的通项公式；

60.设数列{an}是单调递增的等比数列,Sn为数列{an}的前n项和。已知S3=13,且a1+3,3a2,a3+5构成等差数列。

(1)求an及Tn。

(2)是否存在常数λ,使得数列{Sn+λ}是等比数列? 若存在,求λ的值；若不存在,试说明理由。

61.已知等差数列{an}满足a2=3,a5=9,数列{bn}满足b1=2,bn+1=abn。

(1)求数列{an}和{bn}的通项公式；

(2)若cn=an·(bn-1),求数列{cn}的前n项和Tn。

62.已知等差数列{an}的前n项和为Sn,满足S3=12,且a1,a2,a4成等比数列。

(1)求an及Sn；

63.已知等差数列{an},等比数列{bn},满足a1=b1=1,a2+b2=,且a3=-10b2。

(1)求数列{an}及数列{bn}的通项公式；

(2)设cn=|an·bn|,求数列{cn}的前n项和Tn。

64.数列{an}为正项数列,Sn是其前n项和,a1=2,且对任意n∈N*,都有：

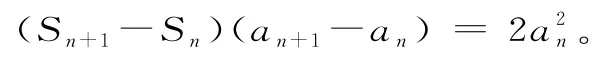
(1)求数列{an}的通项公式；

(2) 若数列 {bn} 满 足bn=,求数列{bn}的前n项和Tn。

65.已知正项等比数列{an}中,a4=81,且a2,a3的等差中项为

(1)求数列{an}的通项公式；

(2)若bn=log3a2n-1,数列{bn}的前n项和为Sn,数列{cn}满足,Tn为数列{cn}的前n项和,证明Tn＜。

66.已知数列{an}满足a1=1,,其中n∈N*。

67.若数列{an}的前n项和Sn=2an-2。

(1)求数列{an}的通项公式；

68.已知数列{an}的前n项和为Sn,且Sn=2an-2n-1。

(1)求数列{an}的通项公式；