全国名校解三角形测试题(A卷)
2019-09-28河南省汝阳县第一高级中学刘俊报
■河南省汝阳县第一高级中学 刘俊报
一、选择题
1.在△ABC中,下列等式正确的是( )。
A.a:b=A:B
B.a:b=sinA:sinB
C.a:b=sinB:sinA
D.asinA=bsinB
2.在△ABC中,已知,则角A为( )。
A.30° B.60° C.120° D.150°
3.在△ABC中,内 角A,B,C满 足,则cos 2A=( )。

4.以下关于正弦定理或其变形的叙述错误的是( )。
A.在 △ABC中,a:b:c=sinA:sinB:sinC
B.在 △ABC中,若 sin 2A=sin 2B,则a=b
C.在 △ABC中,若sinA>sinB,则A>B
D.在 △ABC中,
5.△ABC的内角A、B、C的对边分别为a、b、c,若A=,a=3,b=2,则sinB=( )。

6.在△ABC中,A=60°,b=1,其面积为,则等于( )。
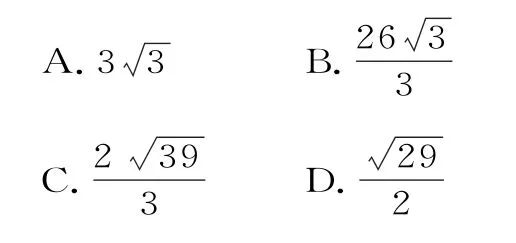
7.在△ABC中,a、b、c分别是角A、B、C的对边,若a=2bcosC,则△ABC的形状是( )。
A.等腰三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
8.在△ABC中,角A、B、C所对的边分别为a、b、c,若a=,b=2,sinB+cosB=,则角A的大小为( )。
A.60° B.30° C.150° D.45°
9.在△ABC中,C=60°,AC=,AB=,则A=( )。
A.15° B.45° C.75° D.105°
10.在△ABC中,B=60°,AD是∠BAC的平分线,且交BC于D,BD=,cos∠BAC=,则AD=( )。

11.在△ABC中,若bcosC+ccosB=asinA,则△ABC的形状为( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
12.△ABC的内角A、B、C的对边分别为a、b、c,根据下列条件解三角形,其中有两解的是( )。
A.a=2,b=3,A=30°
B.b=6,c=4,A=120°
C.a=,b=6,A=60°
D.a=3,b=6,A=30°
13.已知△ABC的内角A、B、C的对边分别为a、b、c,AD为角A的角平分线,且交BC于D,B=,AD=,BD=2,则b=( )。

14.设△ABC的内角A、B、C所对的边分别是a、b、c,且b=3,c=1,A=2B,则a的值为( )。

15.在△ABC中,D是BC边上一点,∠BAD=∠CAD=60°,BD=2CD=4,则tan∠ABC=( )。
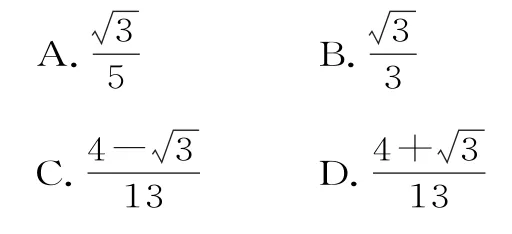
16.在△ABC中,B=,M为AC边上的一点,且BM=2,若BM为∠ABC的角平分线,则的取值范围为( )。

17.在△ABC中,角A、B、C所对的边分别为a、b、c,若△ABC为锐角三角形,且满足b2-a2=ac,则的取值范围是( )。
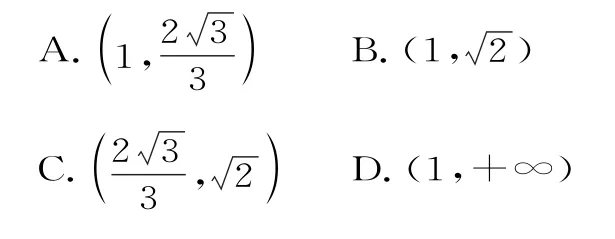
18.在△ABC中,角A、B、C所对的边分别 为a、b、c,若a2tanB=b2tanA,则△ABC的形状为( )。
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
19.在△ABC中,角A、B、C的对边分别为a、b、c,若3bcosC=c(1-3cosB),则sinC:sinA=( )。
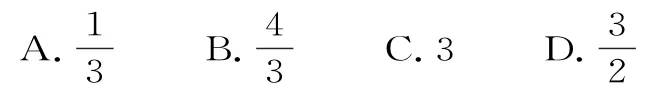
20.如 图 1,在△ABC中,已知A:B=1∶2,CD为∠BCA的平分线,且S△ACD∶S△BCD=3∶2,则cosA等于( )。

图1

21.△ABC中,若,则△ABC中最长的边是( )。
A.aB.bC.cD.b或c
22.在锐角△ABC中,已知a、b、c分别是角A、B、C的对边,且,a=4,则△ABC面积的最大值为( )。

23.已知△ABC的内角A、B、C的对边分别是a、b、c,且(a2+b2-c2)·(acosB+bcosA)=abc。若△ABC的外接圆半径为,则△ABC的周长的取值范围为( )。
A.(2,4] B.(4,6]
C.(4,6) D.(2,6]
24.在△ABC中,角A、B、C所对的边分别为a、b、c,S表示△ABC的面积。若ccosB+bcosC=asinA,S=(b2+a2-c2),则B=( )。
A.90° B.60° C.45° D.30°
25.若△ABC为钝角三角形,其中C为钝角,并且A+C=的取值范围是( )。
A.(1,2) B.(2,+∞)
C.(3,+∞) D.[3,+∞)
26.在△ABC中,C=,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足。若DE=,则cosA=( )。
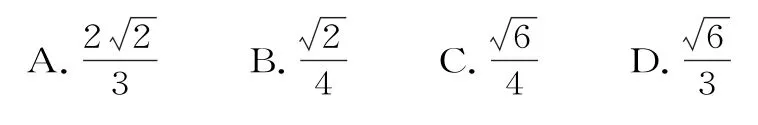
27.在△ABC中,角Α、Β、C所对的边分别为a、b、c,若,且b=,则下列关系一定不成立的是( )。
A.a=cB.b=c
C.2a=cD.a2+b2=c2
28.在△ABC中,已知a=x,b=2,B=60°,如果△ABC有两组解,则x的取值范围是( )。

29.在△ABC中,A=45°,a=λ,b=,那么满足条件的△ABC( )。
A.无解 B.有一个解
C.有两个解 D.不能确定
30.在△ABC中,a、b、c分别为角A、B、C的对边,若△ABC的面积为S,且S=(a+b)2-c2,则。

31.在△ABC中,角A、B、C所对的边分别 是a、b、c,若cosA=,a=3,且△ABC的面积为,则b+c=( )。
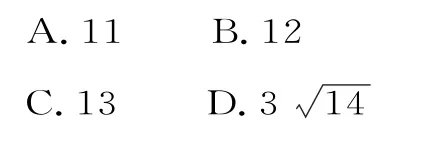
32.平面四边形ABCD中,∠ABC=150°,AB=2BC,AC=13,BD⊥AB,CD=3,则四边形ABCD的面积为( )。

33.在△ABC中,角A、B、C的对边分别为a、b、c,已知,且b2+c2-a2=4,则△ABC的面积为( )。

34.在某个位置测得某山峰仰角为θ,对着山峰在平行地面上前进600 m 后测得仰角为原来的2 倍,继续在平行地面上前进后测得仰角为原来的4 倍,则该山峰的高度为( )。
A.200 m B.300 m
C.400 m D.100 m
35.若△ABC的面积为(a2+c2-b2),且C为钝角,则B的度数以及的取值范围为( )。

36.已知△ABC的三边长是三个连续的自然数,且最大的内角是最小内角的2倍,则最小角的余弦值为( )。

37.某炮兵阵地位于A点,两个观察所分别位于C,D两点,已知△ACD为等边三角形,且DC=。当目标出现在B点(A,B两点位于CD两侧)时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离约为( )。
A.1.1 km B.2.2 km
C.2.9 km D.3.5 km
38.某小区打算将如图2的一直三角形ABC区域进行改建,在三边上各选一点连成等边三角形DEF,在其内建造文化景观。已知AB=20 m,AC=10 m,则△DEF区域内面积(单位:m2)的最小值为( )。

图2
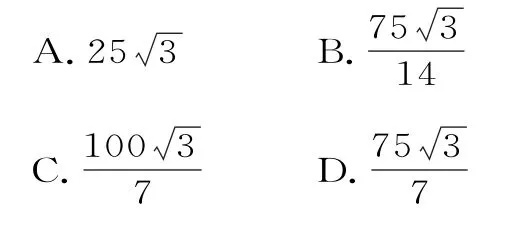
39.赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)。类比“赵爽弦图”,可类似地构造如图3所示的图形,它是由3 个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设DF=2AF,则( )。

图3

二、填空题
40.在△ABC中,角A、B、C所对的边分别为a、b、c,a=2,B=45°,若三角形有两解,则b的取值范围是____。
41.△ABC的三边长是三个连续的自然数,且最大角是最小角的2倍,则此三角形的面积为_____。
42.已知△ABC的边a、b、c的对角分别为A、B、C,若sinA∶sinB∶sinC=1∶∶1,则B=____。
43.若△ABC的周长等于20,面积是,A=60°,则BC边的长是_____。
44.△ABC的内角A、B、C的对边分别为a、b、c。若b=6,a=2c,B=,则△ABC的面积为_____。
45.已知△ABC的边a、b、c的对角分别为A、B、C,若a>b且,则角A的大小为_____。
46.在△ABC中,内角A、B、C的对边分别为a、b、c,若,则B=____。
47.在△ABC中,边a、b、c所对的角分别为A、B、C,若a2=b2+c2-3bc,sinC=2cosB,则A=_____,C=____。
48.在△ABC中,a、b、c分别是角A、B、C的对边,且,则AC边上的高的最大值为____。
49.在锐角三角形ABC中,a、b、c分别为角A、B、C所对的边,且,,且△ABC的面积为,a+b的值为____。
50.在锐角△ABC中,角A、B、C的对边分别为a、b、c。且则a+c的取值范围为____。
51.钝角三角形的三边为a,a+1,a+2,其最大角不超过120°,则a的取值范围是____。
52.在△ABC中,已知BC=8,cosC=,AB边上的中线CD=,则sinB的值为____。
53.在△ABC中,角A、B、C的对边分别为a、b、c,BC边上的高为的最大值是_____。
54.在△ABC中,角A、B、C的对边分别为a、b、c,其中最大的角等于另外两个角的和,当最长边c=1时,△ABC周长的最大值为____。
55.如图4,四边形ABCD中,AB=4,BC=5,CD=3,∠ABC=90°,∠BCD=120°,则AD的长为____。
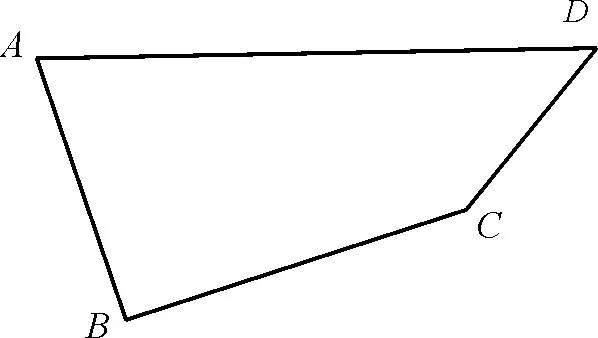
图4
56.已知在△ABC中,∠ABC=90°,AB=3,BC=2,P为△ABC内一点,∠BPC=135°,则AP的最小值为_____。
57.如图5,在平面四边形ABCD中,A=B=C=75°,BC=2,则AB的取值范围是_____。
58.△ABC的内角A、B、C所对的边分別为a、b、c,则下列命题正确的是_____。

图5
①若sinAsinB=2sin2C,则;
②若a+b>2c,则;
③若a4+b4=c4,则△ABC是锐角三角形;
④若(a+b)c<2ab,则。
59.下列是有关△ABC的几个命题:
①若tanA+tanB+tanC>0,则△ABC是锐角三角形;②若acosA=bcosB,则△ABC是等腰三角形;③若acosB+bcosA=b,则△ABC是等腰三角形;④若cosA=sinB,则△ABC是直角三角形。其中所有正确命题的序号是_____。
三、解答题
60.在△ABC中,a、b、c分别是角A、B、C所对的边,且2csinB=3atanA。
(2)如果a=1,且角A最大时,试求△ABC的面积。
61.在△ABC中,角A、B、C的对边分别为a、b、c,且2acosB=2c+b。
(1)求A的大小;
(2)若△ABC的面积为,且其外接圆的半径为,求△ABC的周长。
62.已知△ABC的三个内角A、B、C所对应的边分别为a、b、c,且cos2A+cos2Ccos2B=1-sinAsinC。
(1)求B的大小;
(2)若b=2,求△ABC面积的最大值。
63.如图6,在△ABC中,D是边BC上一点,AB=AC,BD=1,sin ∠CAD=3sin ∠BAD。

图6
(1)求DC的长;
(2)若AD=2,求△ABC的面积。
64.△ABC的内角A、B、C的对边分别为a、b、c,设(sinB-sinC)2=sin2AsinBsinC。
(1)求A的大小;
65.在△ABC中,A、B、C的对边分别a、b、c,A=60°,cosB=。
(1)若D是BC上 的 点,AD平分∠BAC,求的值;
(2)若ccosB+bcosC=2,求△ABC的面积。
66.在△ABC中,角A、B、C的对边分别是a、b、c,且
(1)求角B的值;
(2)若b=且b≤a,求的取值范围。
67.△ABC的内角A、B、C的对边分别为a、b、c,并且
(1)求角B的值;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围。
