正弦定理的八大功能

■湖北省巴东县第三高级中学 廖庆伟

正弦定理：在△ABC中,(R为△ABC的外接圆半径)。

正弦定理是解三角形的重要理论依据之一,解题时要灵活运用,主要有下面八大功能。

一、三角形解的判断

例1在△ABC中,若a=18,b=24,A=45°,则此三角形( )。

A.无解

B.有两解

C.有一解

D.解的个数不确定

解析：因为,所以sinB=sinA=。

又因为a＜b,所以B的值有两个,三角形也有两个。

故选B。

点评：三角形解的判断：

二、求角

例2在△ABC中,角A、B、C所对应的边分别为a、b、c,若a=,b=2,sinB+cosB=,则角A的大小为____。

解析：由sinB+cosB=,得1+2sinBcosB=2,即sin 2B=1。

因为0＜B＜π,所以B=45°。

又因为a=,b=2,所以在△ABC中,由正弦定理得

因为a＜b,所以A＜B=45°,A=30°。

点评：已知两角和一边可求第三角,解这样的三角形只需直接用正弦定理代入求解即可。

已知两边和其中一边的对角,利用正弦定理求另一边的对角时要注意讨论角的范围,这是解题的难点,应引起同学们的注意。

三、求边长

例3已知△ABC的周长为+1,且sinA+sinB=sinC,则AB=____。

解析：由题意及正弦定理,得AB+BC+AC=+1,且BC+AC=AB。

两式相减,解得AB=1。

点评：求值问题的实质还是解三角形,直接用正弦定理把角化成边,本题列方程组可求解。

四、求面积

例4在△ABC中,若AB=,AC=1,B=30°,则△ABC的面积为____。

图1

解析：如图1 所示,由正弦定理,得sinC=。而c＞b,所以C=60°或C=120°。

对应A=90°或A=30°。

点评：三角形中的计算问题归根结底还是解三角形问题,抓住三角形的可解条件,对应问题就迎刃而解。

五、求范围

例5在锐角△ABC中,BC=1,B=2A,则AC的取值范围为____。

解析：由正弦定理得,所以=1,即AC=2cosA。

由锐角△ABC得0°＜2A＜90°,所以0°＜A＜45°。

又0°＜180°-3A＜90°,所以30°＜A＜60°。

故30°＜A＜45°。

故AC=2cosA∈(2,3)。

点评：求解这类问题的关键是把用角A的三角函数表示出来,利用函数y=cosx的性质求解,易错点是判断角A的取值范围。

六、判断三角形的形状

例6在△ABC中,若,则△ABC的形状为____。

解析：由正弦定理,得,即

已知sinA＞0,sinB＞0,则sinAcosA=sinBcosB,即sin 2A=sin 2B。

所以2A=2kπ+2B或2A=2kπ+π-2B(k∈Z)。

因为0＜A＜π,0＜B＜π,所以k=0。

则A=B或A=-B。

△ABC为等腰三角形或直角三角形。

点评：判断三角形的形状的基本思想是利用正弦、余弦定理进行边角的统一,即将条件化为只含角的三角函数关系式,然后利用三角恒等变换得出内角之间的关系式,或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系。

七、正弦定理与余弦定理的综合运用

例7在△ABC中,角A、B、C的对边分别为a、b、c,证 明：。

证明：由余弦定理得：

a2=b2+c2-2bccosA,b2=a2+c2-2accosB。

所以a2-b2=b2-a2-2bccosA+2accosB,整理得

点评：三角形中的有关证明问题基本方法同三角恒等式的证明,但要注意灵活选用正弦定理或余弦定理。

八、用正弦定理解决实际问题

例8如图2 所示,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°,则可以计算出A,B两点的距离为( )。

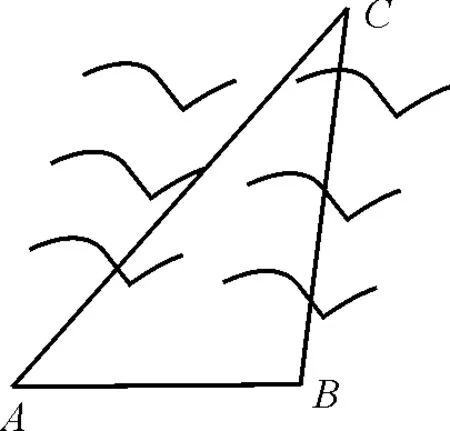
图2

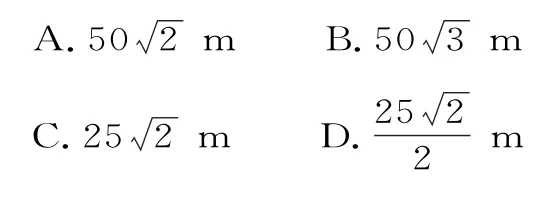
解析：由题意,得B=30°。

点评：解此类问题,首先要弄清题意,合理将条件归结到某一个三角形中处理是常见策略,同时要灵活运用正弦定理及平面几何的相关知识。